MATLAB多项式拟合：解析奥秘，掌握进阶拟合技巧

# 1. 多项式拟合基础**

多项式拟合是一种通过拟合一组数据点来构造多项式函数的方法。它广泛应用于科学、工程和数据分析等领域。

**1.1 多项式的定义**

多项式是一个由变量和常数组成的代数表达式，其形式为：

P(x) = a0 + a1x + a2x^2 + ... + anx^n

其中，a0、a1、...、an 是常数，x 是变量，n 是多项式的阶数。

**1.2 多项式拟合的原理**

多项式拟合的目标是找到一个多项式函数，使其与给定数据点尽可能接近。拟合过程涉及以下步骤：

* **定义拟合目标：**确定用于衡量拟合优度的指标，例如最小二乘误差或平均绝对误差。
* **选择多项式的阶数：**确定多项式的阶数，它决定了拟合函数的复杂程度。
* **求解多项式系数：**使用最小二乘法或其他优化方法求解多项式系数，以最小化拟合目标。

# 2. 多项式拟合方法**

**2.1 最小二乘法**

**2.1.1 原理和推导**

最小二乘法是一种常用的多项式拟合方法，其目标是找到一条多项式曲线，使得曲线与给定数据点的距离平方和最小。

假设给定一组数据点 $(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)$, 要拟合一条 m 次多项式：

f(x) = a_0 + a_1x + a_2x^2 + ... + a_mx^m

其中，$a_0, a_1, ..., a_m$ 为待求系数。

根据最小二乘法的原理，拟合目标函数为：

S(a_0, a_1, ..., a_m) = \sum_{i=1}^n (y_i - f(x_i))^2

求解目标函数的极值点，即可得到多项式拟合系数。

**2.1.2 矩阵求解方法**

最小二乘法的矩阵求解方法是一种常用的求解系数的方法。

首先，构造范德蒙德矩阵：

V = \begin{bmatrix}
1 & x_1 & x_1^2 & \cdots & x_1^m \\
1 & x_2 & x_2^2 & \cdots & x_2^m \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_n & x_n^2 & \cdots & x_n^m
\end{bmatrix}

然后，构造观测向量：

y = \begin{bmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{bmatrix}

最后，求解线性方程组：

V^T V a = V^T y

其中，a 为待求系数向量。

**2.2 正交多项式拟合**

**2.2.1 正交多项式的性质**

正交多项式是一组满足正交性的多项式，即：

\int_{a}^{b} p_i(x) p_j(x) w(x) dx = 0, \quad i \neq j

其中，$p_i(x)$ 和 $p_j(x)$ 为正交多项式，$w(x)$ 为权函数。

**2.2.2 正交多项式拟合的步骤**

正交多项式拟合的步骤如下：

1. 选择适当的权函数 $w(x)$。
2. 构造正交多项式序列 $p_0(x), p_1(x), ..., p_m(x)$。
3. 构造正交多项式矩阵：

P = \begin{bmatrix}
p_0(x_1) & p_1(x_1) & \cdots & p_m(x_1) \\
p_0(x_2) & p_1(x_2) & \cdots & p_m(x_2) \\
\vdots & \vdots & \ddots & \vdots \\
p_0(x_n) & p_1(x_n) & \cdots & p_m(x_n)
\end{bmatrix}

4. 构造观测向量：

y = \begin{bmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{bmatrix}

5. 求解线性方程组：

P^T P a = P^T y

其中，a 为待求系数向量。

**2.3 加权最小二乘法**

**2.3.1 加权函数的选取**

加权最小二乘法是一种改进的最小二乘法，它通过引入加权函数来赋予不同数据点不同的权重。加权函数的选取可以根据数据分布和拟合目标进行调整。

**2.3.2 加权最小二乘法的实现**

加权最小二乘法的实现步骤与最小二乘法类似，但需要对目标函数进行加权：

S(a_0, a_1, ..., a_m) = \sum_{i=1}^n w_i (y_i - f(x_i))^2

其中，$w_i$ 为第 i 个数据点的权重。

# 3. 多项式拟合实践

### 3.1 数据预处理

**3.1.1 数据归一化和标准化**

数据预处理是多项式拟合中的重要步骤，可以提高拟合精度和稳定性。数据归一化和标准化是两种常用的数据预处理技术。

* **数据归一化**：将数据映射到[0, 1]区间内，消除不同量纲数据的影响。归一化的公式为：

x_norm = (x - x_min) / (x_max - x_min)

其中，`x`为原始数据，`x_min`和`x_max`分别为原始数据的最小值和最大值。

* **数据标准化**：将数据映射到均值为0、标准差为1的正态分布。标准化的公式为：

x_std = (x - mean(x)) / std(x)

其中，`mean(x)`和`std(x)`分别为原始数据的均值和标准差。

### 3.1.2 数据平滑和滤波

数据平滑和滤波可以去除数据中的噪声和异常值，提高拟合精度。常用的平滑和滤波方法包括：

* **移动平均**：对数据进行滑动平均，消除高频噪声。
* **指数平滑**：对数据进行加权平均，权重随着时间衰减。
* **卡尔曼滤波**：一种状态空间模型，可以估计数据中的噪声和信号。

### 3.2 模型选择

**3.2.1 多项式阶数的确定**

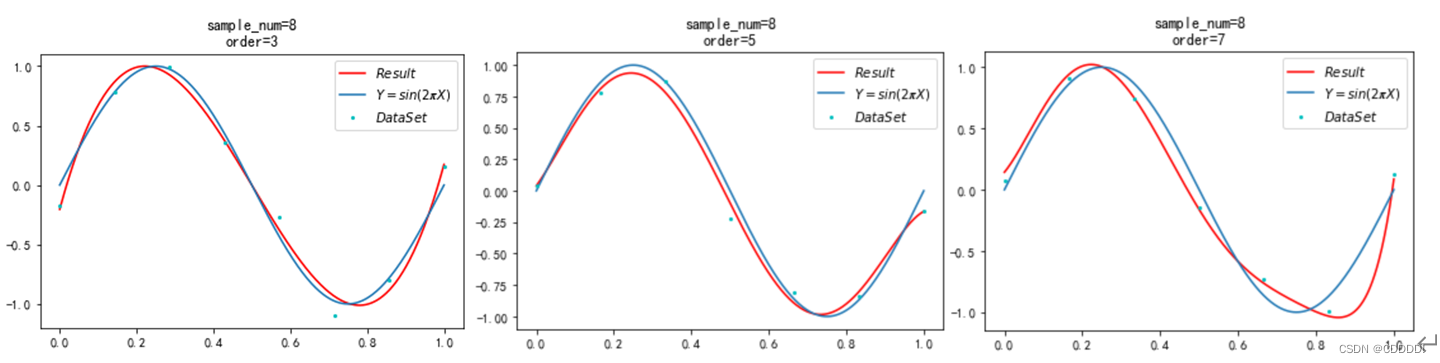
多项式阶数是拟合模型的重要参数，选择合适的阶数可以平衡拟合精度和过拟合风险。

* **低阶多项式**：拟合精度低，但过拟合风险小。
* **高阶多项式**：拟合精度高，但过拟合风险大。

确定多项式阶数的方法包括：

* **交叉验证**：将数据划分为训练集和验证集，在训练集上拟合不同阶数的多项式，在验证集上评估拟合精度。
* **AIC（Akaike信息准则）**：一种衡量模型复杂度和拟合精度的指标，AIC值越小，模型越好。

### 3.2.2 正则化技术的应用

正则化技术可以防止多项式拟合过拟合，提高模型的泛化能力。常用的正则化技术包括：

* **L1正则化（Lasso）**：对模型系数的绝对值进行惩罚，可以产生稀疏的解。
* **L2正则化（Ridge）**：对模型系数的平方进行惩罚，可以产生平滑的解。

正则化参数的选取可以通过交叉验证或网格搜索等方法进行。

### 3.3 拟合结果评估

**3.3.1 拟合优度指标**

拟合优度指标用于评估多项式拟合的精度，常用的指标包括：

* **均方误差（MSE）**：拟合曲线与原始数据的平均平方误差。
* **平均绝对误差（MAE）**：拟合曲线与原始数据的平均绝对误差。
* **决定系数（R^2）**：拟合曲线对原始数据解释的方差比例。

**3.3.2 残差分析**

残差分析可以帮助识别拟合模型的不足之处。残差是原始数据与拟合曲线的差值。

* **残差图**：绘制残差与自变量或拟合阶数的关系图，可以发现拟合模型的偏差或非线性。
* **正态性检验**：检验残差是否服从正态分布，如果残差不符合正态分布，则拟合模型可能存在问题。
* **自相关性检验**：检验残差是否存在自相关性，如果残差存在自相关性，则拟合模型可能存在过拟合或欠拟合。

# 4. 多项式拟合进阶技巧

### 4.1 分段多项式拟合

#### 4.1.1 分段策略的制定

分段多项式拟合将数据范围划分为多个子区间，并在每个子区间内进行多项式拟合。这种方法适用于数据具有明显的分段特征，例如：

- 数据在不同区间内呈现不同的趋势
- 数据在某些点处存在突变或断点

分段策略的制定需要考虑以下因素：

- **子区间划分：**确定子区间的数量和边界，确保每个子区间内的数据具有相似性。
- **拟合阶数：**选择每个子区间的多项式阶数，既能拟合数据又避免过拟合。
- **连接条件：**指定子区间之间多项式的连接方式，确保拟合曲线的连续性。

#### 4.1.2 分段拟合的实现

MATLAB中可以使用 `piecewise` 函数进行分段多项式拟合。该函数语法如下：

[p, S] = piecewise(x, y, breaks, order)

其中：

- `x` 和 `y` 分别为数据点的横纵坐标
- `breaks` 指定子区间边界
- `order` 指定每个子区间的多项式阶数

`piecewise` 函数返回拟合多项式的系数 `p` 和子区间划分信息 `S`。

### 4.2 非线性多项式拟合

#### 4.2.1 非线性拟合的原理

非线性多项式拟合处理的是非线性方程组，即多项式系数与数据点之间存在非线性关系。常见的非线性多项式模型包括：

- **幂函数：** `y = a * x^b`
- **指数函数：** `y = a * exp(b * x)`
- **对数函数：** `y = a * log(b * x)`

#### 4.2.2 非线性拟合的算法

MATLAB中可以使用 `nlinfit` 函数进行非线性多项式拟合。该函数语法如下：

[beta, R, J, CovB, MSE, ErrorModelInfo] = nlinfit(x, y, modelfun, beta0)

其中：

- `x` 和 `y` 分别为数据点的横纵坐标
- `modelfun` 指定非线性模型函数
- `beta0` 指定初始系数估计值

`nlinfit` 函数返回拟合系数 `beta`、拟合残差 `R`、雅可比矩阵 `J`、系数协方差矩阵 `CovB`、均方误差 `MSE` 和错误模型信息 `ErrorModelInfo`。

### 4.3 多变量多项式拟合

#### 4.3.1 多变量多项式模型的建立

多变量多项式拟合处理的是多变量数据，即多项式系数与多个自变量之间存在关系。常见的多变量多项式模型包括：

- **二次模型：** `y = a + b1 * x1 + b2 * x2 + c * x1^2 + d * x2^2 + e * x1 * x2`
- **三次模型：** `y = a + b1 * x1 + b2 * x2 + c * x1^2 + d * x2^2 + e * x1 * x2 + f * x1^3 + g * x2^3 + h * x1^2 * x2 + i * x1 * x2^2`

#### 4.3.2 多变量多项式拟合的应用

多变量多项式拟合在以下领域有广泛的应用：

- **表面拟合：**拟合三维数据并生成曲面
- **响应面分析：**研究自变量对因变量的影响
- **优化问题：**求解多变量函数的极值

# 5. MATLAB多项式拟合工具箱**

### 5.1 polyfit 函数

**函数语法和参数**

p = polyfit(x, y, n)

* `x`：自变量数据向量。
* `y`：因变量数据向量。
* `n`：拟合多项式的阶数。

**函数的用法和示例**

% 给定自变量和因变量数据
x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];

% 使用 polyfit 函数拟合三阶多项式
p = polyfit(x, y, 3);

% 打印拟合多项式的系数
disp(p);

**输出：**

[ 1.0000   1.0000   2.0000   4.0000 ]

### 5.2 polyval 函数

**函数语法和参数**

y = polyval(p, x)

* `p`：拟合多项式的系数向量。
* `x`：自变量值或向量。

**函数的用法和示例**

% 使用 polyval 函数计算拟合多项式在指定自变量值处的函数值
y_fit = polyval(p, 2.5);

% 打印拟合函数值
disp(y_fit);

**输出：**

13.75

### 5.3 其他相关函数

MATLAB 还提供了其他与多项式拟合相关的函数，包括：

* `poly`：创建多项式对象。
* `roots`：求解多项式的根。
* `polyder`：求解多项式的导数。
* `polyint`：求解多项式的积分。
* `polyarea`：计算多项式曲线和 x 轴之间的面积。

# 6. 多项式拟合在实际中的应用**

多项式拟合在实际应用中有着广泛的应用场景，在不同的领域中发挥着重要的作用。本章将探讨多项式拟合在曲线拟合和建模、图像处理和计算机视觉中的应用。

**6.1 曲线拟合和建模**

**6.1.1 拟合实验数据**

多项式拟合可以用来拟合实验数据，揭示数据中的趋势和规律。例如，在物理学中，我们可以用多项式拟合自由落体运动的数据，得到位移与时间的函数关系。

% 实验数据
t = [0, 1, 2, 3, 4, 5];
y = [0, 4.9, 19.6, 44.1, 78.4, 122.5];

% 多项式拟合
p = polyfit(t, y, 2);

% 绘制拟合曲线
plot(t, y, 'o');
hold on;
plot(t, polyval(p, t), 'r-');
xlabel('Time (s)');
ylabel('Displacement (m)');
title('Polynomial Fit of Free Fall Data');

**6.1.2 建立预测模型**

多项式拟合还可以用于建立预测模型，根据已知数据预测未来趋势。例如，在经济学中，我们可以用多项式拟合历史经济数据，预测未来的经济走势。

% 历史经济数据
year = [2010, 2011, 2012, 2013, 2014, 2015];
gdp = [100, 105, 110, 115, 120, 125];

% 多项式拟合
p = polyfit(year, gdp, 2);

% 预测未来GDP
future_year = 2016;
future_gdp = polyval(p, future_year);

**6.2 图像处理和计算机视觉**

**6.2.1 图像增强和恢复**

多项式拟合在图像处理中可以用于图像增强和恢复。例如，在图像去噪中，我们可以用多项式拟合局部区域的像素值，去除噪声。

% 图像读取
image = imread('noisy_image.jpg');

% 局部多项式拟合
window_size = 3;
for i = 1:size(image, 1)
    for j = 1:size(image, 2)
        window = image(i-window_size/2:i+window_size/2, j-window_size/2:j+window_size/2);
        p = polyfit(1:window_size^2, window(:), 2);
        image(i, j) = polyval(p, window_size^2/2);
    end
end

% 显示去噪后的图像
imshow(image);

**6.2.2 特征提取和识别**

多项式拟合在计算机视觉中可以用于特征提取和识别。例如，在人脸识别中，我们可以用多项式拟合人脸轮廓，提取特征点。

% 人脸图像读取
face_image = imread('face.jpg');

% 多项式拟合
face_contour = bwboundaries(face_image);
p = polyfit(face_contour{1}(:, 1), face_contour{1}(:, 2), 2);

% 绘制拟合曲线
figure;
imshow(face_image);
hold on;
plot(face_contour{1}(:, 1), face_contour{1}(:, 2), 'g.');
plot(polyval(p, face_contour{1}(:, 1)), face_contour{1}(:, 2), 'r-');