Python回归模型：5个实战案例带你深入理解线性回归

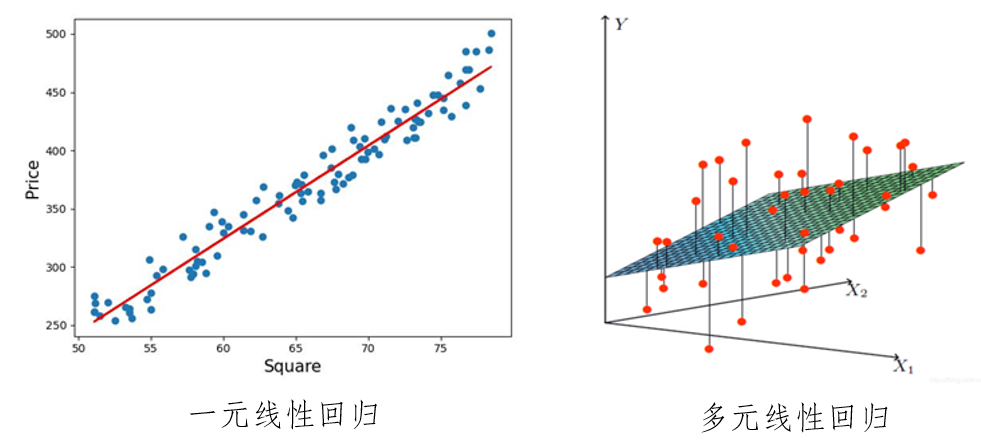
# 1. 线性回归模型概述

线性回归是统计学中研究变量间线性关系的建模方法，广泛应用于数据科学、经济预测、工程分析等领域。在机器学习中，线性回归属于监督学习算法，它利用输入变量与输出变量之间的线性关系来建立模型，预测连续值输出。本章将简要介绍线性回归模型的基本概念，并对后续章节进行概览，为读者进一步深入研究线性回归算法打下基础。

# 2. 线性回归的数学基础

线性回归是统计学和机器学习中最基础的模型之一。它被广泛应用于预测和解释数据中的线性关系。要掌握线性回归模型，首先需要理解其背后的数学原理和相关的假设条件。在本章中，我们将深入探讨线性回归的数学基础，为后续的模型构建、诊断和优化奠定坚实的理论基础。

### 2.1 线性回归的数学原理

#### 2.1.1 线性模型定义

在数学上，线性回归模型试图找到一个线性方程来描述因变量 \( Y \) 和自变量 \( X_1, X_2, \dots, X_p \) 之间的关系。该方程可以表示为：

\[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \dots + \beta_pX_p + \epsilon \]

这里，\( Y \) 是因变量，\( X_1, X_2, \dots, X_p \) 是 \( p \) 个自变量，\( \beta_0, \beta_1, \dots, \beta_p \) 是模型参数，而 \( \epsilon \) 是误差项，代表模型未能解释的随机变异部分。

#### 2.1.2 参数估计和最小二乘法

参数 \( \beta \) 的估计是通过最小化误差项 \( \epsilon \) 的平方和来完成的，这就是所谓的最小二乘法。数学上，我们希望最小化以下目标函数：

\[ S = \sum_{i=1}^{n} (Y_i - (\beta_0 + \beta_1X_{i1} + \dots + \beta_pX_{ip}))^2 \]

其中，\( n \) 是观测值的数量，\( Y_i \) 和 \( X_{ij} \) 分别是第 \( i \) 个观测值的因变量和第 \( j \) 个自变量的值。为了找到最佳的 \( \beta \) 值，需要对 \( S \) 关于 \( \beta \) 求偏导并令其为零，然后求解这个线性方程组。

### 2.2 线性回归的假设条件

在实际应用中，线性回归模型对数据有一些基本的假设。了解和检验这些假设是评估模型是否适用的关键。

#### 2.2.1 线性关系假设

线性回归的基本假设是因变量和每个自变量之间存在线性关系。如果关系是非线性的，线性模型可能无法准确捕捉数据的真实模式。

#### 2.2.2 多重共线性问题

当模型中的自变量之间存在高度相关时，会出现多重共线性问题，这可能导致参数估计不稳定和不可靠。解决多重共线性问题的一种方法是采用岭回归或LASSO回归等正则化技术。

#### 2.2.3 异方差性和自相关性问题

异方差性指的是误差项的方差不是恒定的，而自相关性则意味着误差项之间存在相关关系。这两种情况都会违反线性回归的假设，对参数估计的准确性和模型的推断产生影响。对于这些问题，可以采用稳健的回归技术或进行数据变换来缓解。

为了更直观地理解线性回归模型的数学基础，下面将展示一个简单的Python代码示例，它使用最小二乘法来估计参数。

import numpy as np
import statsmodels.api as sm

# 生成模拟数据
np.random.seed(0)
X = np.random.rand(100, 1)
X = sm.add_constant(X)  # 添加截距项
beta = np.array([1, 2])  # 参数真值
epsilon = np.random.randn(100)
y = np.dot(X, beta) + epsilon

# 使用最小二乘法进行参数估计
model = sm.OLS(y, X).fit()
print(model.summary())

在上述代码中，我们首先生成了一个模拟数据集，然后使用 `statsmodels` 库中的 `OLS` 类来拟合线性模型，并输出了模型的摘要信息，包括参数的估计值、标准误差、\( t \) 值和 \( p \) 值等统计信息。

线性回归模型的数学基础是理解和应用该模型的前提。下一章我们将探讨如何使用Python等工具来构建和诊断线性回归模型。

# 3. 线性回归模型的实现

## 3.1 使用Python构建线性回归模型

### 3.1.1 导入必要的库和数据

构建线性回归模型的第一步是准备环境和数据。在Python中，我们通常使用`pandas`库来处理数据，`numpy`来进行数学运算，而`scikit-learn`库提供了强大的机器学习工具，包括线性回归模型。以下是一个导入数据和库的基本示例：

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# 假设数据集以.csv文件格式存储
data = pd.read_csv('data.csv')

# 查看数据集的前几行
print(data.head())

# 分离特征和标签
X = data.drop('target_column', axis=1) # 特征
y = data['target_column']               # 标签（预测目标）

在这个代码块中，首先导入了必要的库，并加载了数据集。然后，我们使用`drop()`函数分离出标签列和特征列。注意，我们以`target_column`代替了实际的列名，这需要你根据数据集的情况替换。

### 3.1.2 模型的训练与预测

在准备好了数据之后，我们可以继续训练线性回归模型，并使用它进行预测。接下来的步骤包括分割数据集、训练模型以及进行预测：

# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建线性回归实例
linear_regressor = LinearRegression()

# 训练模型
linear_regressor.fit(X_train, y_train)

# 进行预测
y_pred = linear_regressor.predict(X_test)

在上面的代码中，`train_test_split()`函数用于将数据集分为训练集和测试集。设置`test_size=0.2`表示测试集将占总数据的20%。`random_state=42`是用于数据分割时的随机种子，确保每次运行代码时都能得到相同的结果。然后创建了一个`LinearRegression`实例，并用训练集数据来拟合模型。最后，使用`predict()`方法来进行预测。

## 3.2 线性回归模型的诊断

### 3.2.1 残差分析

残差分析是线性回归模型诊断的一个重要环节。残差是实际观测值与模型预测值之间的差异。理想情况下，残差应该呈现随机分布，没有明显的模式。下面是如何在Python中进行残差分析：

residuals = y_test - y_pred

import matplotlib.pyplot as plt
plt.scatter(linear_regressor.predict(X_train), residuals)
plt.title('Residuals vs. Fitted')
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.show()

在上面的代码段中，我们首先计算了残差，然后使用`matplotlib`库绘制了残差图。如果残差随机分布在零线两侧，那么模型可能就表现良好。反之，如果残差呈现出某种明显的模式，可能说明模型存在问题，比如非线性关系未被捕捉，或者存在异方差性。

### 3.2.2 模型的评估指标

模型的评估指标对于理解模型性能至关重要。以下是线性回归常用的几个评估指标的计算：

# 均方误差 (Mean Squared Error, MSE)
mse = mean_squared_error(y_test, y_pred)
print('Mean Squared Error:', mse)

# 决定系数 (Coefficient of Determination, R^2)
r2 = r2_score(y_test, y_pred)
print('R^2 Score:', r2)

均方误差（MSE）衡量的是预测值与实际值之差的平方和的平均值。理想情况下，MSE应该尽可能小。决定系数（R^2）是反映模型拟合优度的指标，其值的范围是0到1之间，越接近1表示模型的解释能力越强。

### 3.2.3 模型的优化策略

根据模型的评估结果，我们可能需要对模型进行优化。一个常见的优化策略是特征选择，它可以提高模型的解释力和性能。以下是如何利用`SelectKBest`进行特征选择的示例：

from sklearn.feature_selection import SelectKBest, f_regression

# 选择最佳的k个特征
k_best_features = SelectKBest(f_regression, k='all')
X_new_train = k_best_features.fit_transform(X_train, y_train)
X_new_test = k_best_features.transform(X_test)

# 再次训练模型
linear_regressor_optimized = LinearRegression()
linear_regressor_optimized.fit(X_new_train, y_train)

# 进行预测
y_pred_optimized = linear_regressor_optimized.predict(X_new_test)

# 计算优化后的性能指标
mse_optimized = mean_squared_error(y_test, y_pred_optimized)
r2_optimized = r2_score(y_test, y_pred_optimized)
print('Optimized Mean Squared Error:', mse_optimized)
print('Optimized R^2 Score:', r2_optimized)

在此代码块中，`SelectKBest`类用于选择最佳的`k`个特征。我们将`k`设置为'all'表示选择所有特征，但也可以根据评分选择一个更小的数。然后，我们用选定的特征重新训练模型并评估其性能。性能的提升可以说明特征选择是有益的。

通过本章节的介绍，我们可以看到在Python中构建和优化线性回归模型的过程。从数据准备、模型训练、诊断分析到模型评估和优化，每一步都离不开对数据的深入理解和对模型性能的严谨评估。通过不断的实践和探索，我们可以提升模型的预测准确性，使其更好地服务于我们的业务需求。

# 4. 实战案例分析

## 4.1 案例一：房价预测

在房价预测这个案例中，我们将通过实际数据来演示如何应用线性回归模型。该案例包括以下几个主要步骤：数据准备和探索、模型的构建和评估。

### 4.1.1 数据准备和探索

首先，我们需要收集与房价相关的数据，通常这包括房屋的大小、位置、建造年份、卧室数量等特征。接下来，我们对数据进行清洗，确保数据质量，处理缺失值，并进行初步的数据探索分析。

import pandas as pd
import numpy as np

# 假设我们已经获取了包含房屋特征和相应房价的数据集
data = pd.read_csv('housing_data.csv')

# 查看数据集的前几行，了解数据结构
print(data.head())

# 检查数据类型和缺失值
print(***())

# 数据探索分析
import matplotlib.pyplot as plt
import seaborn as sns

sns.pairplot(data)
plt.show()

通过查看`***()`我们可以发现是否有任何特征包含缺失值。`pairplot`可以帮助我们可视化不同特征之间的关系，识别可能的线性关系。

### 4.1.2 模型的构建和评估

构建模型的第一步是划分数据集为训练集和测试集。然后我们选择合适的特征和目标变量（即房屋价格），使用训练集数据训练模型，并用测试集数据评估模型性能。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 数据预处理，选择特征和目标变量
X = data.drop(['price'], axis=1)
y = data['price']

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 构建线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 预测测试集数据
y_pred = model.predict(X_test)

# 评估模型性能
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')

# 使用模型进行单个预测
single_pred = model.predict([[size, bedrooms, bathrooms, location_score]])
print(f'Predicted house price: {single_pred[0]}')

在上述代码块中，我们首先导入了`train_test_split`和`LinearRegression`等库来执行数据划分和模型构建。接着使用`fit`方法训练模型，并用`predict`方法进行预测。最后，使用`mean_squared_error`函数评估了模型的均方误差。

## 4.2 案例二：股票市场分析

在股票市场分析中，线性回归可以帮助我们理解不同变量之间的关系，例如股价与公司业绩、市场趋势等因素。

### 4.2.1 数据获取和预处理

首先，我们需要获取股票市场的数据，包括股票的历史价格、交易量、基本面数据等。然后进行数据清洗和预处理，包括数据对齐、处理缺失值和异常值等。

### 4.2.2 建立线性回归模型

建立模型时，我们可能需要对时间序列数据进行特殊处理，例如添加滞后变量。此外，股票价格可能随时间展现出非线性趋势，线性回归可能需要与其他模型结合使用。

## 4.3 案例三：信用评分

信用评分系统是金融机构用来评估贷款申请人违约风险的重要工具。通过历史数据的分析，线性回归模型可以帮助我们预测贷款违约的概率。

### 4.3.1 数据集介绍和特征选择

信用评分数据集通常包含申请人的年龄、性别、婚姻状况、收入、债务、信用历史等信息。特征选择是构建有效模型的关键步骤，需要考虑特征与目标变量的相关性和信息量。

### 4.3.2 模型的训练和结果分析

构建模型后，我们通过训练集数据来训练模型，并在测试集上验证模型的准确性。结果分析可能包括违约预测的准确率、召回率等指标。

# 使用逻辑回归作为分类器，将问题转化为二分类问题
from sklearn.linear_model import LogisticRegression

# 特征和目标变量
X = data.drop(['default'], axis=1)
y = data['default']

# 训练集和测试集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 建立逻辑回归模型
logreg = LogisticRegression()
logreg.fit(X_train, y_train)

# 预测
y_pred = logreg.predict(X_test)

# 结果分析
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))

在上述代码块中，我们首先选取了特征和目标变量，然后将数据集分割成训练集和测试集。使用`LogisticRegression`进行信用评分模型的构建，并通过`predict`方法进行预测。最后，使用`classification_report`输出了分类结果的详细报告，包括精确度、召回率、F1分数等指标。

通过上述三个案例的分析，我们可以看到线性回归模型在实际问题中的应用。在实际操作中，可能需要进行更复杂的数据预处理和特征工程，以适应具体的业务需求。此外，对模型的评估和优化也至关重要，以确保模型在现实世界中的有效性。

# 5. 线性回归的进阶应用

在深入探讨了线性回归的基本概念、数学原理以及模型实现之后，我们现在可以探索一些更高级的主题，这些主题将帮助我们更好地理解和应用线性回归模型。本章将介绍多变量线性回归和与其他机器学习算法的比较，这些都是在实际应用中经常遇到的高级话题。

## 5.1 多变量线性回归

### 5.1.1 模型建立和参数解释

多变量线性回归是线性回归在多个自变量情况下的扩展。它允许我们同时考虑多个因素对因变量的影响。在多变量线性回归中，模型的一般形式可以表示为：

\[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n + \epsilon \]

其中，\( Y \)是因变量，\( X_1, X_2, ..., X_n \)是自变量，\( \beta_0 \)是截距项，而\( \beta_1, \beta_2, ..., \beta_n \)是对应于每个自变量的系数。

以Python为例，我们可以使用`scikit-learn`库中的`LinearRegression`类来建立多变量线性回归模型。下面的代码展示了如何实现这一点：

from sklearn.linear_model import LinearRegression

# 假设 X 是一个二维数组，其中包含多个特征，y 是目标变量
model = LinearRegression()
model.fit(X, y)

在模型训练完成后，`model.coef_`属性可以用来查看每个特征的系数，而`model.intercept_`则给出了截距项的值。理解每个系数的含义对模型解释至关重要，因为它们代表了自变量变化一个单位对目标变量的平均影响。

### 5.1.2 模型的正则化处理

当我们处理包含大量特征的数据集时，模型可能会出现过拟合现象，即模型在训练数据上表现良好，但在未知数据上表现较差。为了解决这个问题，我们可以使用正则化方法，如L1正则化（Lasso回归）或L2正则化（Ridge回归）来减少模型复杂度。

Lasso回归通过向损失函数添加一个绝对值惩罚项来减少一些系数的大小，甚至将某些不重要的系数压缩到零，从而实现特征选择的目的。

Ridge回归通过添加一个平方惩罚项来控制系数的大小，这有助于减少模型对噪声数据的敏感性。

下面是一个使用`scikit-learn`库中`Ridge`类实现Ridge回归的例子：

from sklearn.linear_model import Ridge

# 设置正则化强度参数 alpha
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X, y)

在这里，`alpha`参数控制正则化的强度，它是一个重要的超参数，通常需要通过交叉验证来选择最佳值。

## 5.2 线性回归与其他机器学习算法的比较

在机器学习领域，线性回归并不是唯一的建模选择。与其他机器学习算法相比，线性回归在某些方面有着独特的优势，但也有其局限性。接下来，我们将探索线性回归与其他算法的比较。

### 5.2.1 与决策树和随机森林的比较

决策树是一种常见的非线性模型，它通过创建决策规则来对数据进行分割。随机森林是决策树的一种集成方法，它通过构建多个决策树并进行投票或平均来改进性能。

线性回归和决策树的主要区别在于模型的形式和假设。线性回归假设数据之间存在线性关系，而决策树能够捕捉更复杂的关系，如决策边界是多边形而不是直线。线性回归通常更容易解释，而决策树可能更难解释，因为它们创建的是一个多层次的分支结构。

随机森林作为决策树的集成方法，通常比单个决策树模型表现更好，尤其是在处理高维数据时。然而，它也更难解释。

### 5.2.2 与支持向量机的比较

支持向量机（SVM）是一种强大的分类器，它试图找到最优的决策边界，以最大化不同类别之间的间隔。当使用线性核时，SVM可以看作是一种线性模型，但这并不限制它只能在特征空间中进行线性分割。

线性回归和SVM之间的主要区别在于目标。线性回归的目标是找到一个能够最小化预测误差的线性方程，而SVM的目标是找到能够最好地区分类别的决策边界。此外，SVM在处理非线性问题时具有优势，因为它可以使用核技巧将数据映射到高维空间。

下面是一个使用`scikit-learn`库中`SVC`类实现SVM的例子：

from sklearn.svm import SVC

# 创建一个支持向量分类器实例
svc = SVC(kernel='linear')
svc.fit(X_train, y_train)

在这段代码中，`kernel`参数决定了使用的核函数类型，`linear`表示线性核。

通过上述比较，我们可以看到，线性回归在解释性、数据处理速度方面有其优势，但在处理非线性关系时可能不如其他算法灵活。选择合适的算法需要考虑具体问题的需要，以及数据集的特性。在实践中，最好的做法是尝试多种模型，并通过交叉验证等技术选择最佳模型。

# 6. 线性回归模型的未来展望

在深入了解线性回归模型后，我们进入了一个由数据驱动决策的时代。尽管线性回归作为一个经典的统计方法，在处理现实世界问题时仍显示出强大的生命力，但其局限性和未来的发展方向也是值得关注的。

## 6.1 模型的局限性与挑战

线性回归模型的成功依赖于数据质量、模型假设的正确性以及适用场景。然而，在面对复杂的数据结构和非线性关系时，传统的线性回归便显得力不从心。下面列出几个常见的局限性：

- **非线性关系处理**：如果变量之间的关系并非线性，线性回归模型很难准确地捕捉到这种关系。
- **异常值影响**：线性回归对异常值非常敏感，一个离群点就可能极大地改变模型参数的估计。
- **多重共线性**：当解释变量之间高度相关时，会增大参数估计的不确定性。
- **异方差性和自相关性**：违反线性回归中关于残差的假设，可能导致估计的标准误差不准确。

为应对这些挑战，数据科学家开发出多种技术，如在模型中加入多项式项来处理非线性关系，使用鲁棒回归来减少异常值的影响，以及借助岭回归和LASSO来解决多重共线性问题。

## 6.2 线性回归在新兴领域的应用

随着技术的发展和数据可用性的增加，线性回归模型正被应用到新兴领域，并与其他技术相结合以适应更复杂的问题。以下是线性回归的一些新用途：

- **金融行业**：在信用评分和风险管理中，线性回归模型被用来预测贷款违约率和投资回报。
- **健康科学**：在医学研究中，线性回归帮助分析疾病与各种风险因素之间的关系。
- **交通物流**：线性回归用于预测运输需求和优化物流网络。
- **社会科学**：通过线性回归分析社会经济指标与人类行为之间的相关性。

这些应用突出了线性回归的灵活性，以及它如何与领域知识结合产生洞见。

## 6.3 持续学习和资源推荐

为了进一步提升对线性回归模型的理解和应用能力，持续学习是不可或缺的。以下是一些推荐资源和学习途径：

- **在线课程**：如Coursera、edX提供的统计和机器学习课程，经常包含线性回归的深入讲解。
- **技术文档和指南**：了解线性回归在特定统计包中的实现，如R语言的`lm()`函数或Python中的`scikit-learn`库。
- **专业社区**：加入如Kaggle、Stack Overflow等平台，与其他数据科学爱好者互动，学习他们是如何解决实际问题的。
- **学术论文和书籍**：关注最新的学术研究可以了解线性回归的前沿应用和理论进展。《An Introduction to Statistical Learning》是推荐给任何希望加强统计学习理论基础的读者的书。

通过这些途径，线性回归的学习者可以不断提升自己的知识和技能，为解决更复杂的问题做好准备。