Python回归模型调参技巧：网格搜索与随机搜索的实战指南

# 1. Python回归模型调参概述

回归分析是数据分析和机器学习领域中的一项核心技术，它允许我们根据历史数据预测未来的趋势。调参，即调整模型的超参数，是优化回归模型性能的关键步骤。Python作为机器学习的热门语言之一，其强大的库如Scikit-learn等提供了丰富的调参工具，可以帮助我们自动化调整过程，从而提高模型预测的准确率。本章将简要概述回归模型调参的必要性、常见方法，以及如何在Python中进行调参。

## 1.1 回归模型调参的意义

在回归分析中，模型的性能不仅仅取决于数据质量和特征选择，还很大程度上依赖于超参数的设置。超参数是控制学习过程和模型复杂度的外部配置，它们不是通过训练过程自动确定的。调参是一个试错过程，其目的是找到一组超参数，使得模型在未知数据上的表现最佳。

## 1.2 Python调参的常用方法

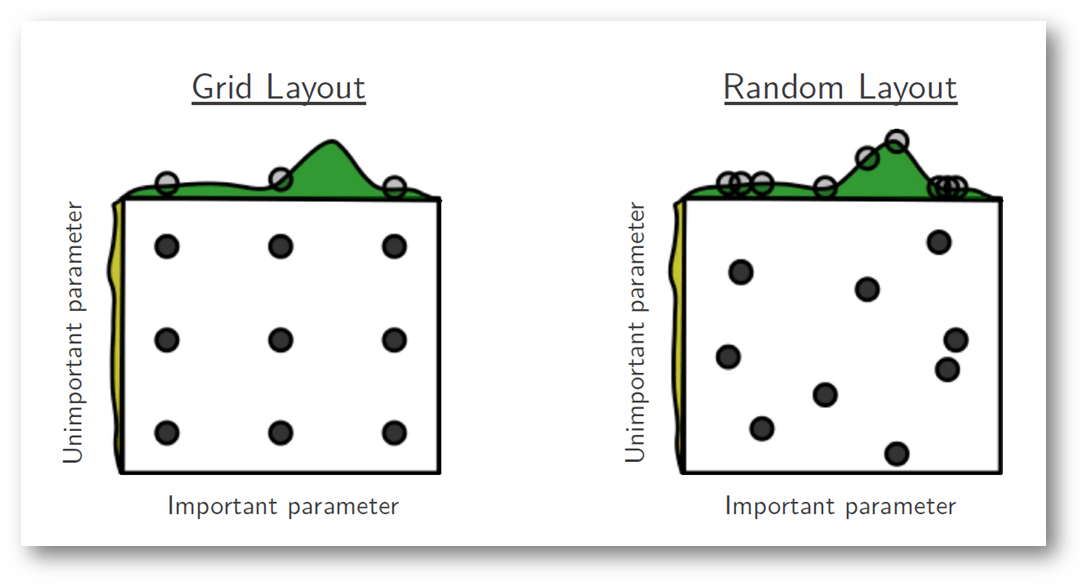
Python中进行回归模型调参的常用方法包括网格搜索（Grid Search）、随机搜索（Random Search）和贝叶斯优化等。其中，网格搜索是最直观的方法，它遍历预定义的参数组合，以确定最佳配置。随机搜索则在参数空间中随机选择参数组合进行测试，相较于网格搜索更节省计算资源。贝叶斯优化则是一种更为智能的搜索方式，它基于已有的评估结果来指导下一步的搜索方向。

## 1.3 Python调参工具概览

Python的机器学习库提供了多种调参工具。Scikit-learn是一个广泛使用的机器学习库，它提供了`GridSearchCV`和`RandomizedSearchCV`等工具，分别对应网格搜索和随机搜索。此外，对于更高级的调参需求，可以使用如`Hyperopt`、`Optuna`等第三方库，它们提供了更加强大和灵活的调参策略。通过这些工具的使用，可以显著提升回归模型的性能。

在接下来的章节中，我们将深入探讨理论基础、网格搜索技术、随机搜索技术以及调参工具，为Python回归模型调参提供全面的技术支持。

# 2. 理论基础与网格搜索技术

## 2.1 回归模型的基本概念和应用场景

### 2.1.1 线性回归

线性回归是最基础的回归模型之一，它的目的是确定两个或更多个变量之间是否存在线性关系，并找到这种关系的最佳拟合线。在简单线性回归中，我们通常有一个自变量x和一个因变量y，我们尝试找到一个线性方程来描述它们的关系：

y = β0 + β1x + ε

其中，β0是截距，β1是斜率，ε是误差项。在机器学习中，线性回归模型可以用于预测连续值输出，如股票价格预测、房屋价格评估和温度变化分析等领域。

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np

# 创建模拟数据
X = np.random.rand(100, 1)
y = 2 * X.squeeze() + 1 + np.random.randn(100) * 0.1

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 初始化线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 预测测试集
y_pred = model.predict(X_test)

# 打印模型参数
print(f"Coefficient: {model.coef_}")
print(f"Intercept: {model.intercept_}")

在上面的代码中，我们使用了`sklearn.linear_model`中的`LinearRegression`类来创建一个线性回归模型，并使用模拟数据对其进行训练和测试。模型的参数`model.coef_`和`model.intercept_`分别表示斜率和截距。线性回归模型参数通常通过最小二乘法来确定，目标是最小化预测值与实际值之间的平方差。

### 2.1.2 逻辑回归

尽管名称中有“回归”两字，但逻辑回归实际上是一种分类算法，常用于二分类问题。它通过逻辑函数（通常是sigmoid函数）将线性回归模型的输出映射到0和1之间，从而得到概率值。逻辑回归模型的形式如下：

p = 1 / (1 + exp(-(β0 + β1x)))

其中p表示正类的概率。逻辑回归通过最大化似然函数来估计模型参数。

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification

# 创建模拟的二分类数据
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, random_state=42)

# 初始化逻辑回归模型
model = LogisticRegression()

# 训练模型
model.fit(X, y)

# 获取模型的系数和截距
print(f"Coefficients: {model.coef_}")
print(f"Intercept: {model.intercept_}")

在该代码段中，我们使用`sklearn.linear_model`中的`LogisticRegression`类来创建一个逻辑回归模型，并用模拟的分类数据进行训练。模型的参数`model.coef_`和`model.intercept_`分别表示特征权重和截距。逻辑回归广泛应用于信贷风险评估、医学诊断等领域。

## 2.2 网格搜索技术的原理与实践

### 2.2.1 网格搜索的基本步骤

网格搜索是一种穷举搜索方法，用于通过遍历预定义的参数值组合来寻找最优的模型参数。它主要由以下几个步骤组成：

1. **确定参数范围**：首先，针对每个超参数设定一个候选值的范围。
2. **生成所有组合**：创建一个参数网格，每个维度对应一个超参数，并为每个维度生成所有可能的参数值组合。
3. **模型验证**：对于每个参数组合，使用交叉验证方法来训练和评估模型。
4. **选择最优组合**：在所有可能的参数组合中，选择能够带来最佳性能评估分数的那组参数。

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 设置参数范围
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [1, 0.1, 0.01, 0.001],
    'kernel': ['rbf']
}

# 初始化SVM分类器
svc = SVC()

# 初始化GridSearchCV对象
grid_search = GridSearchCV(svc, param_grid, refit=True, verbose=2)

# 进行网格搜索
grid_search.fit(X_train, y_train)

# 输出最佳参数组合
print(f"Best parameters: {grid_search.best_params_}")

以上代码展示了如何使用`sklearn.model_selection`中的`GridSearchCV`类对支持向量机（SVM）模型进行参数优化。首先定义了一个参数网格`param_grid`，其中包含了要优化的超参数C和gamma，以及所使用的核函数类型。`GridSearchCV`会遍历这个网格中的所有参数组合，并返回最优参数组合`grid_search.best_params_`。

### 2.2.2 网格搜索的优缺点分析

网格搜索技术虽然简单易行，但其也存在一些局限性：

**优点**：

1. **系统性搜索**：确保覆盖所有可能的参数组合，不会遗漏潜在的最佳参数组合。
2. **易于实现**：在大多数机器学习框架中均有现成的实现，如`GridSearchCV`。
3. **灵活性**：可以通过定制化参数网格来适应不同的需求和场景。

**缺点**：

1. **计算代价高**：尤其是参数组合数量较多时，网格搜索的计算成本非常高。
2. **参数空间过大时不可行**：对于高维度的参数空间，网格搜索可能变得不切实际。
3. **效率低下**：每组参数的评估是串行进行的，没有充分利用多核处理器的优势。

为了提高效率，我们可能需要考虑采用随机搜索或贝叶斯优化等其他调参方法。

## 2.3 网格搜索的参数优化策略

### 2.3.1 超参数空间的选择

超参数空间的选择直接关系到网格搜索的效率和效果。在选择超参数空间时，以下几点策略值得考虑：

1. **基于先验知识**：根据已有的知识或经验，设定可能的超参数值范围，避免不必要的大范围搜索。
2. **使用领域知识**：了解不同超参数的作用和模型的特点，可以帮助缩小搜索空间。
3. **初步探索**：先进行一个较为粗略的网格搜索，获得对超参数敏感度的大致了解，随后再针对性地细化搜索。

### 2.3.2 交叉验证与模型评估

在网格搜索过程中，为了提高模型性能评估的准确性，通常会采用交叉验证的方法。通过将数据分为k个子集，轮流使用其中的一个子集作为测试集，其他作为训练集来训练和验证模型。这种方法可以帮助我们减少模型对特定数据集的过拟合风险，增加模型泛化能力的可靠评估。

交叉验证有多种类型，例如k折交叉验证、留一交叉验证等。在网格搜索中，`GridSearchCV`已经内置了交叉验证的功能，我们可以直接通过设置`cv`参数来选择交叉验证的类型。

from sklearn.model_selection import KFold

# 初始化K折交叉验证对象
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# 传递KFold对象到GridSearchCV
grid_search = GridSearchCV(svc, param_grid, cv=kf, refit=True, verbose=2)

# 进行网格搜索
grid_search.fit(X_train, y_train)

在这个例子中，我们使用了`KFold`类创建了一个5折交叉验证对象，并将其传递给`GridSearchCV`对象。通过这种方法，每次模型验证都会使用不同的训练集和验证集组合，从而能够更加全面地评估模型的性能。

通过以上方法，网格搜索技术可以在理论基础上得到有效的应用，并通过实践来验证其在超参数优化中的效果。

# 3. 随机搜索技术与高级调参技巧

随机搜索技术是继网格搜索之后的另一种流行的参数优化方法。它在处理大型超参数空间和优化成本高昂的模型时表现尤其突出。本章节将深入探讨随机搜索技术的工作机制，并与网格搜索