处理回归分析中的异常值：Python识别与应对的4大策略

# 1. 回归分析与异常值概述

回归分析是数据分析中广泛应用的技术，它用于估计变量间的关系。然而，在数据分析过程中，异常值（outliers）常常对回归分析的结果产生显著的影响。异常值可能由于数据录入错误、测量错误或自然变异而产生，它们可能导致模型参数估计偏差，降低预测准确性，因此识别和处理异常值是数据分析和建模的关键步骤。

异常值的存在不仅扭曲回归分析结果，还可能掩盖数据的真实趋势。因此，理解异常值及其对回归模型的影响对于任何数据科学项目都是至关重要的。本章将探讨异常值的概念、它们在回归分析中的作用及其潜在的负面影响，为后续章节中异常值识别与处理的方法奠定基础。

# 2. 异常值识别的方法与实践

在数据科学领域，识别和处理异常值是一个至关重要的步骤。异常值可能会扭曲分析结果，导致预测模型出现偏差。本章将探讨多种异常值识别的方法，并提供实际应用案例。

## 2.1 统计学方法

统计学方法是识别异常值的传统方式，其中最常用的是Z-分数和四分位数间距（IQR）。

### 2.1.1 Z-分数（标准分数）

Z-分数是通过计算数据点偏离平均值的标准差的个数来确定的。公式为：

Z = (X - μ) / σ

其中，`X`是观察值，`μ`是平均值，`σ`是标准差。一般来说，Z-分数大于3或小于-3的点被认为是异常值。

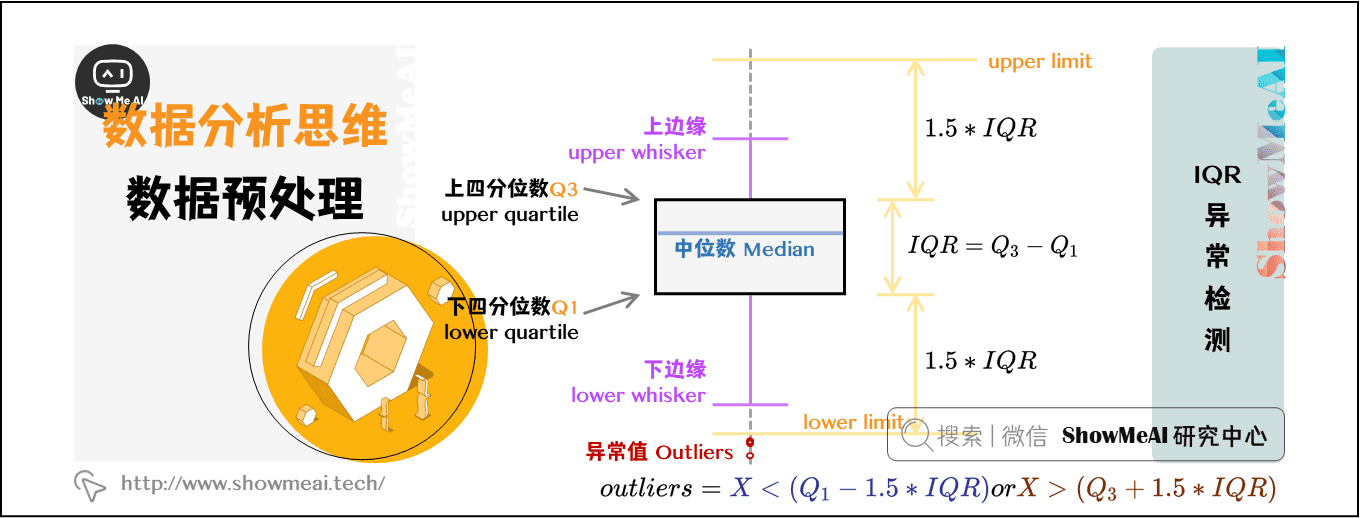
### 2.1.2 四分位数间距（IQR）

IQR是第三四分位数（Q3）与第一四分位数（Q1）的差值。异常值通常被定义为小于Q1 - 1.5*IQR或大于Q3 + 1.5*IQR的值。

IQR = Q3 - Q1

接下来的代码块将展示如何使用Python的Pandas库和SciPy库来计算Z-分数和IQR，并识别异常值。

import pandas as pd
from scipy import stats

# 示例数据
data = pd.Series([10, 12, 12, 13, 12, 11, 14, 19, 21, 22, 23, 22, 18, 15, 16])

# 计算Z-分数
z_scores = stats.zscore(data)
abs_z_scores = pd.Series(abs(z_scores))
filtered_entries = abs_z_scores[(abs_z_scores > 3)]

# 计算IQR
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
outliers = data[(data < (Q1 - 1.5 * IQR)) | (data > (Q3 + 1.5 * IQR))]

print(f"Z-Score Method outliers: {filtered_entries}")
print(f"IQR Method outliers: {outliers}")

在上述代码中，我们首先创建了一个示例数据集，然后计算了每个数据点的Z-分数。接着，我们识别了绝对值Z-分数大于3的数据点作为异常值。对于IQR方法，我们首先计算了第一和第三四分位数，然后识别了低于Q1 - 1.5*IQR或高于Q3 + 1.5*IQR的数据点作为异常值。

## 2.2 图形识别方法

图形识别方法，如散点图和盒须图，通过可视化手段帮助识别异常值。

### 2.2.1 散点图

散点图通过在坐标轴上绘制数据点，直观地展示数据分布情况。异常值通常表现为远离其他数据点的点。

### 2.2.2 盒须图

盒须图是一种基于五数概括（最小值、第一四分位数、中位数、第三四分位数和最大值）的图形表示方法，能够直观地显示数据的分布情况。异常值通常显示为单独的小圆圈或星号。

下面的代码使用Matplotlib库来绘制示例数据的散点图和盒须图。

import matplotlib.pyplot as plt

# 绘制散点图
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.scatter(range(len(data)), data)
plt.title('Scatter Plot')
plt.xlabel('Index')
plt.ylabel('Value')

# 绘制盒须图
plt.subplot(1, 2, 2)
data.plot(kind='box')
plt.title('Boxplot')

plt.show()

在以上代码中，我们首先创建了一个散点图，接着创建了一个盒须图，两者均使用相同的示例数据集。通过这些图形，我们可以直观地识别出可能的异常值。

## 2.3 基于模型的方法

基于模型的方法利用统计模型的残差来识别异常值。

### 2.3.1 使用标准残差

标准残差是实际观测值与模型预测值之间差异的标准分数。在标准残差图中，绝对值大于3的点通常被认为是异常值。

### 2.3.2 使用异常度量（Outlier measure）

异常度量方法如DBSCAN（基于密度的空间聚类应用与噪声），通过数据点的局部密度估计识别异常值。

from sklearn.neighbors import NearestNeighbors
from sklearn.cluster import DBSCAN

# 使用DBSCAN识别异常值
neighbors = NearestNeighbors(n_neighbors=2)
neighbors_fit = neighbors.fit(data.values.reshape(-1, 1))
distances, indices = neighbors_fit.kneighbors(data.values.reshape(-1, 1))

# 计算每个点的最近邻距离
distances = np.sort(distances, axis=0)
distances = distances[:, 1]
plt.plot(distances)
plt.title('Distances to Nearest Neighbors')
plt.xlabel('Data Points sorted by Distance')
plt.ylabel('Distance')
plt.show()

在上述代码中，我们使用`NearestNeighbors`来计算每个点的最近邻距离，然后使用DBSCAN算法来识别可能的异常值。异常点通常具有比邻近点更大的距离。

以上章节展示了异常值识别的各种方法，并提供了详细的代码实现和逻辑分析。在下一章节中，我们将探讨异常值处理的基本策略。

# 3. 异常值处理的基本策略

## 3.1 删除异常值
异常值的简单删除方法是直接移除在数据集中被视为异常的数据点。这种策略适用于单变量数据，并且基于一个明确的阈值，例如，使用Z-分数超过3或IQR方法确定的异常值。然而，这种方法可能会导致信息的丢失，特别是当异常值是由重要过程变化引起的时候。

### 3.1.1 简单删除方法
简单删除方法通过设定阈值来过滤数据，例如，Z-分数大于3的点可能被认为是异常的，并从数据集中删除。这种方法的前提是数据必须满足正态分布，因为Z-分数是基于正态分布理论。

import pandas as pd
from scipy import stats

# 假设有一个Pandas DataFrame数据集df，其中的列名为"feature"
z_scores = stats.zscore(df['feature'])
abs_z_scores = abs(z_scores)
filtered_entries = (abs_z_scores < 3)
df_filtered = df[filtered_entries]

#