回归模型诊断：Python中的模型评估与准确性提升策略

# 1. 回归模型诊断概述

回归模型诊断是机器学习中的一项重要任务，它涉及到检验模型的假设、评估模型的拟合优度以及确保模型的预测准确性。本章将简要介绍回归模型诊断的目的和重要性，为后续章节中对模型评估指标、残差分析和假设检验等深入探讨打下基础。

回归模型诊断的核心目的是发现模型存在的问题，比如错误的假设、过拟合、欠拟合以及可能影响模型性能的异常值。通过对模型进行诊断，我们能够更好地理解模型的行为，提高模型预测的可靠性，并为模型优化提供方向。这不仅可以应用于统计分析，也是数据科学和机器学习领域不可或缺的一部分。

# 2. 模型评估基础

### 2.1 回归模型评估指标

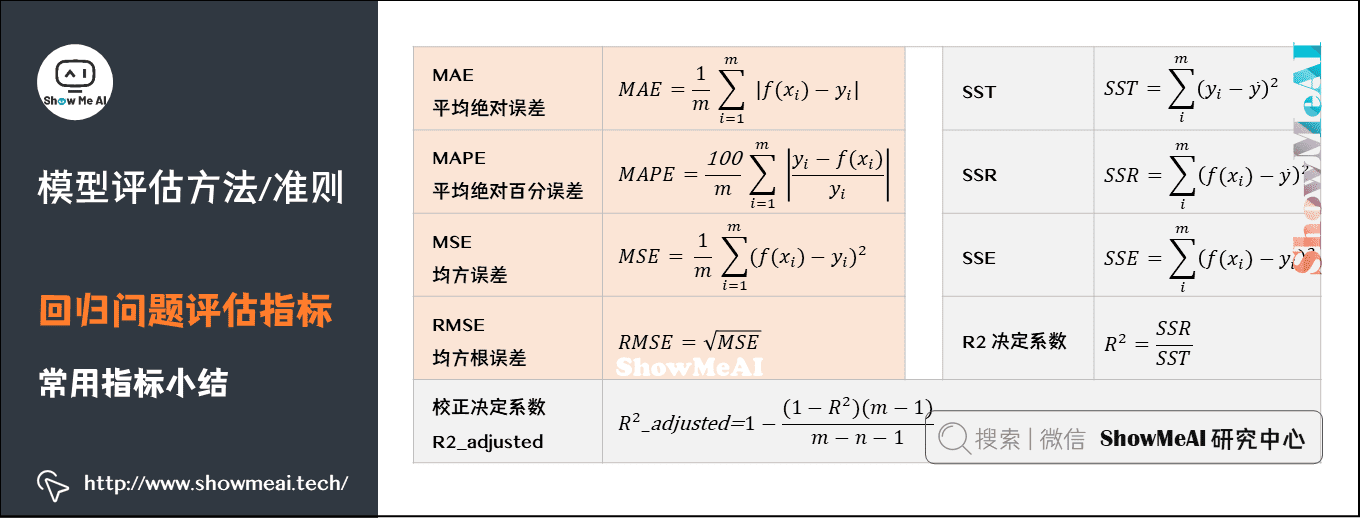
#### 2.1.1 均方误差（MSE）和均方根误差（RMSE）

均方误差（MSE）和均方根误差（RMSE）是回归分析中用于衡量模型预测误差的两个常用指标。MSE是预测值和实际值之差的平方的平均值，而RMSE是MSE的平方根。

from sklearn.metrics import mean_squared_error
from math import sqrt

# 假设y_true是真实值的数组，y_pred是预测值的数组
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]

# 计算MSE
mse = mean_squared_error(y_true, y_pred)

# 计算RMSE
rmse = sqrt(mse)

print(f"MSE: {mse}")
print(f"RMSE: {rmse}")

代码解释：
- `mean_squared_error` 函数计算真实值和预测值之间的均方误差。
- `sqrt` 函数用于计算均方误差的平方根。

参数说明：
- `y_true`: 真实值的数组。
- `y_pred`: 预测值的数组。

逻辑分析：
MSE 和 RMSE 的计算方法简单，但它们对于异常值很敏感，因为误差是被平方的。在评估回归模型时，通常会结合其他指标，如决定系数（R²），来获得更全面的性能视图。

#### 2.1.2 决定系数（R²）

决定系数（R²）衡量的是模型对真实结果变异性的解释程度。R² 的值介于0到1之间，越接近1表示模型的预测能力越强。如果R²为负，表明模型的预测效果比使用平均值作为预测还差。

from sklearn.metrics import r2_score

# 假设y_true是真实值的数组，y_pred是预测值的数组
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]

# 计算R²值
r2 = r2_score(y_true, y_pred)

print(f"R²: {r2}")

代码解释：
- `r2_score` 函数计算真实值和预测值之间的决定系数。

参数说明：
- `y_true`: 真实值的数组。
- `y_pred`: 预测值的数组。

逻辑分析：
R² 是模型性能的一个重要指标，但它也有局限性。特别是当模型中添加更多的变量时，R² 通常会增加，即使这些变量可能对预测目标变量的实际价值没有多少贡献。

### 2.2 残差分析

#### 2.2.1 残差的定义和可视化

在回归分析中，残差是预测值与实际观测值之间的差。通过残差的可视化，我们可以检查数据中是否存在模式或结构，这可能表明模型存在某些问题。

import matplotlib.pyplot as plt
import numpy as np

# 假设y_true是真实值的数组，y_pred是预测值的数组
y_true = np.array([3, -0.5, 2, 7])
y_pred = np.array([2.5, 0.0, 2, 8])

# 计算残差
residuals = y_true - y_pred

# 绘制残差图
plt.scatter(y_pred, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.show()

代码解释：
- 我们首先计算残差，即真实值与预测值之间的差值。
- 使用散点图将预测值与残差对应起来绘制。
- 添加一条水平的红色虚线表示残差为零的位置，便于观察残差分布。

参数说明：
- `y_true`: 真实值的数组。
- `y_pred`: 预测值的数组。

逻辑分析：
如果残差分布呈现出明显的模式或结构，这通常意味着模型可能存在问题。例如，如果残差随着预测值的增加而系统地变化，则表明模型可能违反了同方差性假设。

#### 2.2.2 异常值和强影响点的识别

异常值和强影响点是影响回归模型性能的重要因素。异常值是与其它观测数据明显不同的数据点，而强影响点是那些即使不显著，但也会极大地改变回归线位置和斜率的点。

from statsmodels.graphics.regressionplots import plot_leverage_resid2

# 假设X是自变量数组，y_true是因变量数组，y_pred是预测值数组
# X = ...（自变量数据）
# y_true = ...（真实值数组）
# y_pred = ...（预测值数组）

# 绘制杠杆值和残差平方图
fig, ax = plt.subplots(figsize=(8, 6))
fig = plot_leverage_resid2(ax, X, y_true, y_pred)

plt.show()

代码解释：
- `plot_leverage_resid2` 函数来自statsmodels库，可以同时绘制杠杆值和残差平方图。

参数说明：
- `X`: 自变量数组。
- `y_true`: 真实值数组。
- `y_pred`: 预测值数组。

逻辑分析：
杠杆值图可以帮助我们识别那些在自变量空间中距离较远的点（即潜在的强影响点），而残差平方图则揭示了残差的分布情况。结合这两张图，我们可以更准确地定位出异常值和强影响点，并进一步分析它们对模型性能的影响。

# 3. 诊断回归模型的假设

## 3.1 线性假设检验

### 3.1.1 线性关系的可视化检验

在回归模型中，线性假设检验是确保模型预测能力的基础。线性关系的可视化检验是初步判断线性关系是否存在的一种简单直观方法。通常，我们会绘制预测变量（自变量）和因变量之间的散点图，以及添加拟合线（回归线）来评估关系的线性特征。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 假设数据集，实际情况下应替换为真实数据
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 3, 5, 7, 11])

model = LinearRegression()
model.fit(X, y)

# 绘制散点图和拟合线
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X), color='red')
plt.title('Linear Regression Fit')
plt.xlabel('Independent variable (X)')
plt.ylabel('Dependent variable (y)')
plt.show()

在上述代码中，我们首先创建了一个简单的数据集，并使用线性回归模型拟合这些数据。然后，我们绘制了数据点和拟合线。如果数据点紧贴拟合线，那么可以初步认为线性关系成立。如果数据点分布呈现明显的非线性模式，那么可能需要考虑非线性模型或者对变量进行转换。

### 3.1.2 回归统计检验方法

除了可视化检验外，我们还可以使用统计检验方法来检验线性关系。在统计学中，最常用的检验方法之一是 t-检验。t-检验是用来检验单个系数是否显著不同于0的方法。如果一个系数的p值小于预设的显著性水平（通常是0.05），那么我们可以拒绝系数等于0的原假设，认为该系数在统计上是显著的。

from scipy import stats

# 假设线性回归模型的结果
# coefficients: [intercept, slope]
coefficients = [model.intercept_, model.coef_[0]]
# t-values for coefficients
t_values = coefficients / model.coef_.std误

# 假设显著性水平
alpha = 0.05

# 计算p-values
p_values = [2*(1 - stats.t.cdf(np.abs(t), df=4)) for t in t_values]

# 输出系数和对应的p值
for coef, p_val in zip(coefficients, p_values):
    print(f"Coefficient: {coef}, P-value: {p_val}")

在上述代码段中，我们使用scipy库中的t分布函数计算了系数的t值，并据此得到p值。最后，我们将系数与其p值一同打印出来，以确定每个变量在模型中的重要性。

## 3.2 正态性和同方差性检验

### 3.2.1 残差的正态性检验

正态性假设要求残差（真实值与预测值之间的差）应该近似正态分布。检验残差的正态性对于确保回归模型的统计假设是重要的。Q-Q图（Quantile-Quantile Plot）是检验正态性的常用工具之一。

from statsmodels.graphics.gofplots import qqplot

# 计算残差
residuals = y - model.predict(X)

# 绘制Q-Q图
qqplot(residuals, line='s')
plt.title('Normal Q-Q Plot')
plt.show()

在上面的代码中，我们计算了残差，并使用statsmodels库中的qqplot函数绘制了Q-Q图。如果残差点接近于45度线，我们可以认为残差是正态分布的；否则，可能存在偏离。

### 3.2.2 残差的同方差性检验

同方差性假设是指在所有水平的预测变量下，残差的方差都是相同的。检验同方差性的常用方法是使用残差对预测值或拟合值的散点图。

# 绘制残差对拟合值的散点图
plt.scatter(model.predict(X), residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.title('Residuals vs F