MATLAB FFT与金融建模：傅里叶变换在金融数据分析与预测中的应用，洞察市场趋势

# 1. MATLAB FFT 的基础理论

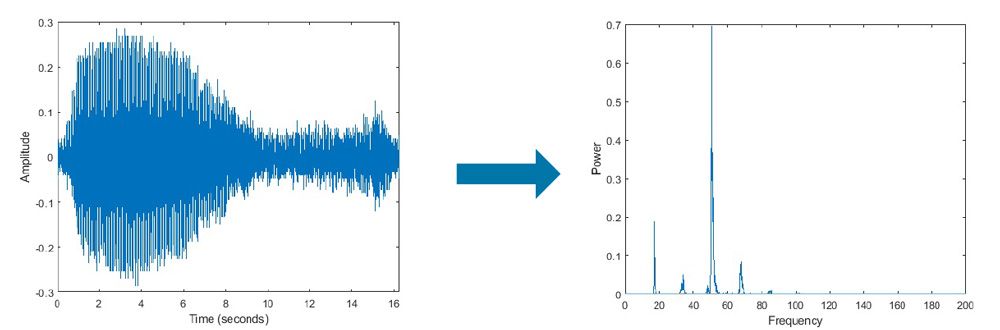
MATLAB FFT（快速傅里叶变换）是一种用于分析和处理时域信号的强大工具。它利用傅里叶变换将信号从时域转换为频域，从而揭示其频率成分。

### 1.1 傅里叶变换的基本原理

傅里叶变换将一个时域信号分解为一系列正弦波和余弦波，每个波都有特定的频率和幅度。通过将信号表示为这些频率分量的总和，傅里叶变换可以揭示信号的频谱特征。

### 1.2 MATLAB FFT 的实现

MATLAB 提供了 `fft()` 函数来执行 FFT。此函数将输入时域信号转换为复数频域表示。频域表示包含信号幅度和相位的复杂值。

# 2. MATLAB FFT 的金融建模应用

### 2.1 金融数据的傅里叶变换

#### 2.1.1 傅里叶变换的基本原理

傅里叶变换是一种数学工具，用于将时域信号分解为其频率分量。对于金融数据，时域信号可以是股票价格、汇率或其他金融变量的时间序列。傅里叶变换将时域信号转换为频域信号，其中频率分量表示为复数。

复数的实部表示信号的幅度，虚部表示信号的相位。幅度表示信号在特定频率下的强度，而相位表示信号在特定频率下的偏移。

#### 2.1.2 金融数据的傅里叶变换特征

金融数据通常具有以下傅里叶变换特征：

* **低频分量：**代表长期趋势和基本面信息。
* **中频分量：**代表周期性模式，例如季节性或周期性波动。
* **高频分量：**代表噪音和随机波动。

### 2.2 FFT 在金融预测中的应用

#### 2.2.1 趋势分析和预测

FFT 可用于识别金融数据的长期趋势。通过分析低频分量，可以识别支撑位和阻力位，并预测未来的价格走势。

% 导入股票价格数据
data = load('stock_prices.csv');

% 计算傅里叶变换
fft_data = fft(data);

% 绘制幅度谱
figure;
plot(abs(fft_data));
xlabel('频率');
ylabel('幅度');

% 识别低频分量
low_freq_idx = find(abs(fft_data) > 0.5);
low_freq_data = data(low_freq_idx);

% 拟合趋势线
p = polyfit(low_freq_idx, low_freq_data, 1);
trendline = polyval(p, low_freq_idx);

% 绘制趋势线
hold on;
plot(trendline, 'r--');
legend('幅度谱', '趋势线');

**代码逻辑分析：**

* `fft(data)` 计算输入数据的傅里叶变换。
* `abs(fft_data)` 取傅里叶变换的幅度。
* `find(abs(fft_data) > 0.5)` 识别幅度大于 0.5 的频率分量，这些分量代表低频趋势。
* `polyfit` 拟合低频分量的一阶多项式，得到趋势线。
* `polyval` 计算趋势线的值。

#### 2.2.2 波动率估计和风险管理

FFT 也可用于估计金融数据的波动率。通过分析中频分量，可以识别波动率的周期性模式，并预测未来的波动率水平。