MATLAB FFT数据分析：傅里叶变换在数据挖掘与预测中的价值，发现隐藏规律

# 1. MATLAB FFT 数据分析简介**

MATLAB 中的 FFT（快速傅里叶变换）是一种强大的工具，用于分析和处理数据中的频率信息。它基于傅里叶变换理论，将时域信号转换为频域表示，揭示了信号中隐藏的频率成分。FFT 在各种领域中都有广泛的应用，包括信号处理、图像处理和数据挖掘。

在本章中，我们将介绍 MATLAB FFT 数据分析的基础知识。我们将探讨傅里叶变换理论的基本原理，包括傅里叶级数、傅里叶变换、DFT 和 FFT。此外，我们将介绍 MATLAB 中 FFT 函数的使用，并演示如何将其应用于实际数据分析场景中。

# 2. 傅里叶变换理论基础

### 2.1 傅里叶级数与傅里叶变换

#### 傅里叶级数
傅里叶级数将周期信号分解为一系列正弦和余弦波的叠加。对于周期为 T 的信号 f(t)，其傅里叶级数表示为：

f(t) = a0 + Σ[an cos(2πnt/T) + bn sin(2πnt/T)]

其中，a0 为直流分量，an 和 bn 为傅里叶系数，可通过以下公式计算：

a0 = (1/T) ∫[0, T] f(t) dt
an = (2/T) ∫[0, T] f(t) cos(2πnt/T) dt
bn = (2/T) ∫[0, T] f(t) sin(2πnt/T) dt

#### 傅里叶变换
傅里叶变换将时域信号 f(t) 转换为频域信号 F(ω)。对于非周期信号，其傅里叶变换定义为：

F(ω) = ∫[-∞, ∞] f(t) e^(-iωt) dt

其中，ω 为角频率。傅里叶变换将信号分解为不同频率成分的叠加，每个频率成分的幅度和相位由 F(ω) 的实部和虚部表示。

### 2.2 时域与频域的转换

时域和频域是信号分析中的两个重要概念。时域表示信号随时间的变化，而频域表示信号中不同频率成分的分布。

#### 时域到频域的转换
傅里叶变换将时域信号转换为频域信号。通过计算傅里叶变换，我们可以获得信号中每个频率成分的幅度和相位信息。

#### 频域到时域的转换
傅里叶逆变换将频域信号转换为时域信号。通过计算傅里叶逆变换，我们可以从频域信息中重建原始时域信号。

### 2.3 离散傅里叶变换 (DFT) 和快速傅里叶变换 (FFT)

#### 离散傅里叶变换 (DFT)
DFT 是傅里叶变换的离散形式，用于处理离散时间信号。对于长度为 N 的离散信号 x[n]，其 DFT 定义为：

X[k] = Σ[n=0, N-1] x[n] e^(-i2πkn/N)

其中，k = 0, 1, ..., N-1。DFT 将离散信号分解为 N 个频率成分，频率间隔为 2π/N。

#### 快速傅里叶变换 (FFT)
FFT 是一种高效的算法，用于计算 DFT。FFT 利用DFT的周期性和对称性，将计算复杂度从 O(N^2) 降低到 O(N log N)。FFT 广泛应用于信号处理、图像处理和数据分析等领域。

# 3. MATLAB FFT 数据分析实践

### 3.1 FFT 函数的使用

MATLAB 提供了 `fft` 函数用于计算离散傅里叶变换 (DFT)。该函数的语法如下：

Y = fft(x)

其中：

* `x` 是一个输入向量，包含要进行傅里叶变换的时域数据。
* `Y` 是一个输出向量，包含 DFT 的结果，以复数形式表示。

`fft` 函数返回的 DFT 结果是一个复数向量，其长度与输入向量相同。实部表示余弦分量，虚部表示正弦分量。

**代码块：**

x = [1, 2, 3, 4, 5];
Y = fft(x);

disp('DFT 结果：');
disp(Y);

**逻辑分析：**

该代码块演示了如何使用 `fft` 函数计算一个向量 `x` 的 DFT。`fft` 函数返回一个复数向量 `Y`，其中实部表示余弦分量，虚部表示正弦分量。

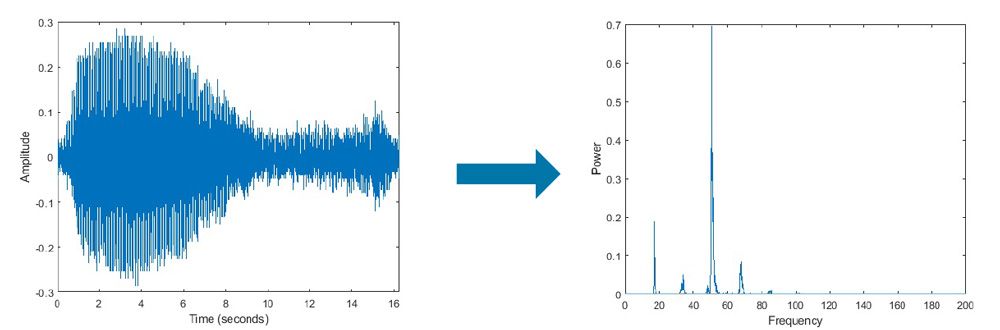
### 3.2 信号频谱分析

傅里叶变换可以用于分析信号的频谱。频谱显示了信号中不同频率分量的幅度和相位。

**频谱图：**

频谱图是一个二维图，横轴表示频率，纵轴表示幅度或功率。频谱图可以显示信号中存在的频率分量及其相对强度。

**代