MATLAB FFT科学计算：傅里叶变换在科学建模与仿真中的应用，探索复杂系统

# 1. MATLAB FFT 科学计算概述

MATLAB FFT（快速傅里叶变换）是一个强大的工具，用于科学计算和工程建模。它将时域信号转换为频域，提供对信号和系统频率成分的深入了解。FFT 在信号处理、图像处理、科学建模和仿真中有着广泛的应用。

FFT 算法利用了傅里叶变换的数学性质，将信号分解为正弦和余弦分量的和。这些分量对应于信号的不同频率，允许对信号的频率内容进行分析和处理。MATLAB 提供了 `fft` 函数，可以高效地执行 FFT，简化了科学计算中的频域分析。

# 2. 傅里叶变换理论基础

### 2.1 傅里叶级数和傅里叶变换

#### 2.1.1 傅里叶级数的定义和性质

傅里叶级数是一种将周期函数表示为正弦和余弦函数的无穷级数的方法。对于周期为 `T` 的函数 `f(t)`，其傅里叶级数为：

f(t) = a_0 + Σ(a_n * cos(2πnt/T) + b_n * sin(2πnt/T))

其中，`a_0` 为常数项，`a_n` 和 `b_n` 为傅里叶系数。傅里叶级数的性质包括：

- **周期性：**傅里叶级数的和函数也是周期为 `T` 的周期函数。
- **收敛性：**傅里叶级数在函数的周期内几乎处处收敛到原始函数。
- **正交性：**傅里叶级数中的正弦和余弦函数正交，即：

∫[0, T] cos(2πnt/T) * cos(2πmt/T) dt = 0, n ≠ m
∫[0, T] sin(2πnt/T) * sin(2πmt/T) dt = 0, n ≠ m
∫[0, T] cos(2πnt/T) * sin(2πmt/T) dt = 0, ∀n, m

#### 2.1.2 傅里叶变换的定义和性质

傅里叶变换是一种将时域信号转换为频域信号的数学运算。对于时域函数 `f(t)`，其傅里叶变换为：

F(ω) = ∫[-∞, ∞] f(t) * e^(-iωt) dt

其中，`ω` 为角频率。傅里叶变换的性质包括：

- **线性性：**傅里叶变换是线性的，即：

F(a*f(t) + b*g(t)) = a*F(f(t)) + b*F(g(t))

- **时移性：**傅里叶变换对时移具有平移性，即：

F(f(t - t0)) = e^(-iωt0) * F(f(t))

- **频率卷积定理：**两个函数的傅里叶变换相乘等于这两个函数时域卷积的傅里叶变换，即：

F(f(t) * g(t)) = F(f(t)) * F(g(t))

### 2.2 傅里叶变换的数学性质

#### 2.2.1 线性性和时移性

傅里叶变换是线性的，即对于任意常数 `a` 和 `b`，以及任意函数 `f(t)` 和 `g(t)`，有：

F(a*f(t) + b*g(t)) = a*F(f(t)) + b*F(g(t))

傅里叶变换还具有时移性，即对于任意常数 `t0`，有：

F(f(t - t0)) = e^(-iωt0) * F(f(t))

#### 2.2.2 频域卷积定理

频域卷积定理是傅里叶变换的一个重要性质，它指出两个函数的傅里叶变换相乘等于这两个函数时域卷积的傅里叶变换，即：

F(f(t) * g(t)) = F(f(t)) * F(g(t))

这个定理在信号处理和图像处理中有着广泛的应用。

### 2.3 傅里叶变换的应用

傅里叶变换在科学计算中有着广泛的应用，包括：

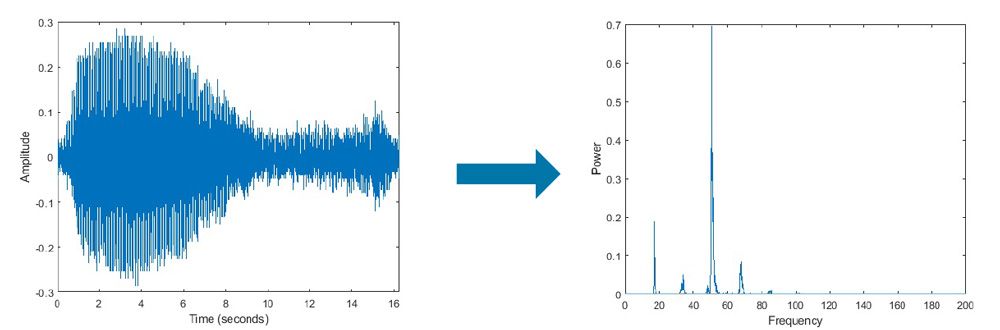
#### 2.3.1 信号分析和处理

傅里叶变换可以用于分析信号的频率成分，从而进行信号处理操作，如滤波、去噪和调制。

#### 2.3.2 图像处理和模式识别

傅里叶变换还可以用于处理图像，如图像锐化、去模糊和模式识别。

# 3. MATLAB FFT 实践应用

### 3.1 FFT 算法和实现

#### 3.1.1 FFT 算法的原理

快速傅里叶