【MATLAB FFT实战指南】：掌握FFT算法，从基础到高级应用

# 1. MATLAB FFT 基础理论

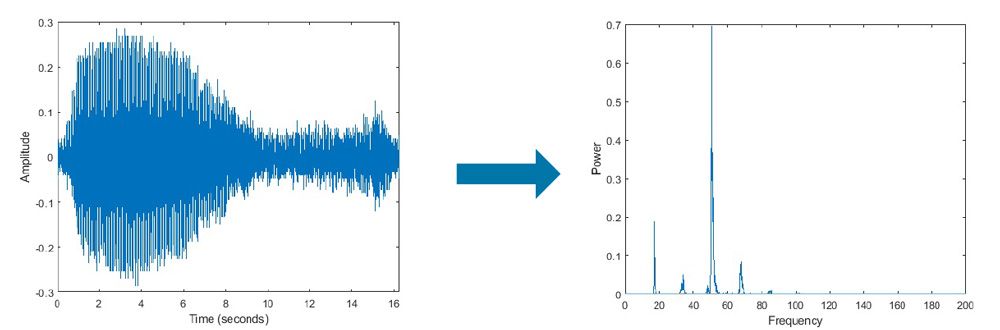
快速傅里叶变换 (FFT) 是一种算法，用于计算离散傅里叶变换 (DFT)。DFT 将时域信号转换为频域信号，从而可以分析信号的频率成分。

FFT 的基本原理是将 DFT 分解为一系列较小的 DFT，然后使用递归算法高效地计算这些较小的 DFT。这大大降低了计算复杂度，使其适用于处理大型数据集。

MATLAB 中的 `fft` 函数用于计算 FFT。该函数接受一个实数或复数向量作为输入，并返回一个包含复数频谱分量的向量。频谱分量的幅度表示信号中每个频率分量的强度，而相位表示信号中每个频率分量的时移。

# 2. MATLAB FFT 算法实现

### 2.1 FFT 算法的原理和步骤

快速傅里叶变换 (FFT) 是一种高效算法，用于计算离散傅里叶变换 (DFT)。DFT 将时域信号转换为频域信号，揭示信号中不同频率分量的幅度和相位信息。

FFT 算法通过将 DFT 分解为一系列较小的、更易于计算的步骤来提高效率。其基本原理是将长度为 N 的输入序列分解为 N 个较小的长度为 2 的子序列，并对每个子序列进行 DFT 计算。然后，将这些子序列的 DFT 结果组合起来得到最终的 DFT 结果。

FFT 算法的具体步骤如下：

1. **分解输入序列：**将长度为 N 的输入序列分解为 N 个长度为 2 的子序列。
2. **计算子序列的 DFT：**对每个子序列进行 DFT 计算，得到子序列的频域表示。
3. **组合子序列的 DFT 结果：**将子序列的 DFT 结果组合起来，得到最终的 DFT 结果。

### 2.2 MATLAB 中的 FFT 函数

MATLAB 提供了两个函数用于计算 FFT：`fft` 函数和 `ifft` 函数。

#### 2.2.1 fft 函数的使用方法

`fft` 函数用于计算 DFT。其语法如下：

Y = fft(x)

其中：

* `x` 是输入时域信号。
* `Y` 是输出频域信号。

#### 2.2.2 ifft 函数的使用方法

`ifft` 函数用于计算 DFT 的逆变换，即将频域信号转换为时域信号。其语法如下：

x = ifft(Y)

其中：

* `Y` 是输入频域信号。
* `x` 是输出时域信号。

### 2.3 FFT 算法的性能分析

#### 2.3.1 时间复杂度分析

FFT 算法的时间复杂度为 O(N log N)，其中 N 是输入序列的长度。这比直接计算 DFT 的时间复杂度 O(N^2) 要高效得多。

#### 2.3.2 内存占用分析

FFT 算法的内存占用与输入序列的长度成正比。对于长度为 N 的输入序列，FFT 算法需要 O(N) 的内存空间。

# 3. MATLAB FFT 实战应用

### 3.1 信号处理中的 FFT 应用

#### 3.1.1 频谱分析

FFT 在信号处理领域中应用广泛，其中一项重要应用就是频谱分析。频谱分析通过计算信号的傅里叶变换，可以将信号分解成一系列频率分量，从而获得信号的频率分布信息。

**步骤：**

1. **获取信号数据：**从信号源获取或导入信号数据。
2. **应用 FFT：**使用 `fft` 函数对信号数据进行傅里叶变换，得到复数频谱数据。
3. **计算幅度谱：**取复数频谱数据的幅度，得到幅度谱，表示信号中各个频率分量的幅度。
4. **绘制频谱图：**将幅度谱绘制成频谱图，展示信号的频率分布。

**代码示例：**

% 导入信号数据
signal = importdata('signal.mat');

% 应用 FFT
fft_result = fft(signal);

% 计算幅度谱
magnitude_spectrum = abs(fft_result);

% 绘制频谱图
figure;
plot(magnitude_spectrum);
title('频谱图');
xlabel('频率');
ylabel('幅度');

**逻辑分析：**

`fft` 函数将信号数据转换为复数频谱数据，其中实部和虚部分别表示频率分量的幅度和相位。`abs` 函数取复数频谱数据的幅度，得到幅度谱，表示各个频率分量的幅度。频谱图展示了幅度谱随频率的变化情况，可以从中分析信号的频率分布特征。

#### 3.1.2 滤波

FFT 还可用于信号滤波。通过在频域上选择性地移除或增强特定频率分量，可以实现滤波效果。

**步骤：**

1. **应用 FFT：**对信号数据进行傅里叶变换，得到复数频谱数据。
2. **设计滤波器：**根据滤波要求设计滤波器，如低通滤波器、高通滤波器或带通滤波器。
3. **应用滤波器：**将滤波器应用于复数频谱数据，保留或移除特定频率分量。
4. **进行逆 FFT：**对滤波后的频谱数据进行逆傅里叶变换，得到滤波后的信号。

**代码示例：**

% 导入信号数据
signal = importdata('signal.mat');

% 应用 FFT
fft_result = fft(signal);

% 设计低通滤波器
cutoff_freq = 100;  % 截止频率
order = 5;          % 滤波器阶数
b = fir1(order, cutoff_freq / (fs / 2));

% 应用滤波器
filtered_fft = fft_result .* b;

% 进行逆 FFT
filtered_signal = ifft(filtered_fft);

% 绘制原始信号和滤波后信号
figure;
subplot(2, 1, 1);
plot(signal);
title('原始信号');
subplot(2, 1, 2);
plot(filtered_signal);
title('滤波后信号');

**逻辑分析：**

`fir1` 函数设计低通滤波器，`.*` 运算将滤波器应用于复数频谱数据，保留低于截止频率的频率分量。`ifft` 函数将滤波后的频谱数据转换为时域信号，得到滤波后的信号。通过绘制原始信号和滤波后信号的对比图，可以观察滤波效果。

### 3.2 图像处理中的 FFT 应用

#### 3.2.1 图像增强

FFT 在图像处理中也有广泛应用，其中一项重要应用就是图像增强。通过在频域上对图像进行处理，可以增强图像的对比度、清晰度和细节。

**步骤：**

1. **读取图像：**读取图像文件并转换为灰度图像。
2. **应用 FFT：**对图像数据进行傅里叶变换，得到复数频谱数据。
3. **图像增强：**在频域上对复数频谱数据进行处理，如高通滤波、低通滤波或锐化处理。
4. **进行逆 FFT：**对处理后的频谱数据进行逆傅里叶变换，得到增强的图像。

**代码示例：**

% 读取图像
image = imread('image.jpg');
image_gray = rgb2gray(image);

% 应用 FFT
fft_result = fft2(image_gray);

% 图像增强：高通滤波
hpf_kernel = ones(3, 3) / 9;
hpf_result = fft2(hpf_kernel) .* fft_result;

% 进行逆 FFT
enhanced_image = ifft2(hpf_result);

% 显示原始图像和增强后图像
figure;
subplot(1, 2, 1);
imshow(image_gray);
title('原始图像');
subplot(1, 2, 2);
imshow(enhanced_image, []);
title('增强后图像');

**逻辑分析：**

`fft2` 函数对图像数据进行二维傅里叶变换，得到复数频谱数据。`.*` 运算将高通滤波器应用于复数频谱数据，增强图像的细节和边缘。`ifft2` 函数将处理后的频谱数据转换为空间域图像，得到增强的图像。通过显示原始图像和增强后图像的对比图，可以观察图像增强效果。

#### 3.2.2 图像压缩

FFT 还可用于图像压缩。通过在频域上对图像进行变换，可以将图像数据压缩到更小的尺寸。

**步骤：**

1. **应用 FFT：**对图像数据进行傅里叶变换，得到复数频谱数据。
2. **量化：**对复数频谱数据进行量化，丢弃高频分量。
3. **进行逆 FFT：**对量化后的频谱数据进行逆傅里叶变换，得到压缩后的图像。

**代码示例：**

% 读取图像
image = imread('image.jpg');
image_gray = rgb2gray(image);

% 应用 FFT
fft_result = fft2(image_gray);

% 量化：丢弃高频分量
quantized_result = fft_result;
quantized_result(abs(quantized_result) < 10) = 0;

% 进行逆 FFT
compressed_image = ifft2(quantized_result);

% 显示原始图像和压缩后图像
figure;
subplot(1, 2, 1);
imshow(image_gray);
title('原始图像');
subplot(1, 2, 2);
imshow(compressed_image, []);
title('压缩后图像');

**逻辑分析：**

`fft2` 函数对图像数据进行二维傅里叶变换，得到复数频谱数据。`quantized_result` 变量将复数频谱数据进行量化，丢弃高频分量，从而压缩图像数据。`ifft2` 函数将量化后的频谱数据转换为空间域图像，得到压缩后的图像。通过显示原始图像和压缩后图像的对比图，可以观察图像压缩效果。

# 4. MATLAB FFT 高级应用

### 4.1 多维 FFT 的实现

#### 4.1.1 多维 FFT 的原理

多维 FFT 是对多维信号或数据进行傅里叶变换的扩展。与一维 FFT 类似，多维 FFT 也将多维信号分解成不同频率分量的叠加。

对于一个 N 维信号 `x(n1, n2, ..., nN)`，其多维 FFT 定义为：

X(k1, k2, ..., kN) = ∑_{n1=0}^{N1-1} ∑_{n2=0}^{N2-1} ... ∑_{nN=0}^{NN-1} x(n1, n2, ..., nN) e^(-j2π(k1n1/N1 + k2n2/N2 + ... + kNnN/NN))

其中：

* `X(k1, k2, ..., kN)` 是多维 FFT 的结果
* `x(n1, n2, ..., nN)` 是多维信号
* `N1, N2, ..., NN` 是信号的维数
* `k1, k2, ..., kN` 是频率分量的索引

#### 4.1.2 MATLAB 中的多维 FFT 函数

MATLAB 提供了 `fftn` 函数来执行多维 FFT。`fftn` 函数的语法如下：

Y = fftn(X)

其中：

* `X` 是输入的多维信号
* `Y` 是输出的多维 FFT 结果

`fftn` 函数支持任意维度的信号。对于一个 N 维信号，`fftn` 函数将返回一个 N 维的 FFT 结果。

### 4.2 快速傅里叶变换 (FFT) 的实现

#### 4.2.1 快速傅里叶变换的原理

快速傅里叶变换 (FFT) 是一种高效的算法，用于计算离散傅里叶变换 (DFT)。DFT 是将时域信号分解成频率分量的数学操作。

FFT 算法通过将 DFT 分解成较小的部分来提高计算效率。它利用了 DFT 的对称性和周期性，将 N 点 DFT 分解成较小的 N/2 点 DFT。

#### 4.2.2 MATLAB 中的快速傅里叶变换函数

MATLAB 提供了 `fft` 函数来执行快速傅里叶变换。`fft` 函数的语法如下：

Y = fft(X)

其中：

* `X` 是输入的时域信号
* `Y` 是输出的频率域信号

`fft` 函数支持任意长度的信号。对于一个长度为 N 的信号，`fft` 函数将返回一个长度为 N/2 + 1 的频率域信号。

### 代码示例

以下代码示例演示了如何使用 MATLAB 执行多维 FFT 和快速傅里叶变换：

% 多维 FFT
x = randn(3, 4, 5); % 创建一个三维信号
X = fftn(x); % 执行多维 FFT

% 快速傅里叶变换
y = randn(1024); % 创建一个一维信号
Y = fft(y); % 执行快速傅里叶变换

# 5. MATLAB FFT 调试与优化

### 5.1 FFT 算法的调试技巧

**5.1.1 常见错误及解决方法**

| 错误 | 原因 | 解决方法 |
|---|---|---|
| FFT 结果为全 0 | 输入数据不包含有效信息 | 检查输入数据是否正确，确保包含非零元素 |
| FFT 结果为全复数 | 输入数据为纯实数 | 使用 `abs(fft(x))` 获取幅度谱 |
| FFT 结果出现 NaN 或 Inf | 输入数据包含 NaN 或 Inf | 检查输入数据，删除或替换无效值 |
| FFT 结果不对称 | 输入数据不为实数 | 使用 `fft(x, 'symmetric')` 进行对称 FFT |

### 5.2 FFT 算法的优化策略

**5.2.1 时间优化**

* **使用快速傅里叶变换 (FFT)：**FFT 算法比直接计算 DFT 更高效。
* **利用对称性：**对于实数输入，FFT 结果是对称的，只需计算一半即可。
* **并行化：**FFT 算法可以并行化，以提高性能。

**5.2.2 内存优化**

* **使用 in-place FFT：**直接在输入数组上进行 FFT 计算，避免创建副本。
* **减少数组大小：**对于大数据集，可以先下采样或压缩数据，然后再进行 FFT。
* **使用高效的数据结构：**选择合适的数组类型（例如，单精度浮点数）和存储顺序（例如，列主序）。

**示例代码：**

% 时间优化：使用快速傅里叶变换
x = randn(100000);
tic;
X = fft(x);
toc;

% 内存优化：使用 in-place FFT
y = randn(100000);
fft(y, [], 1);