【长程作用力计算】：NAMD模拟中的库仑力与范德华力解析


参考资源链接：[NAMD分子动力学模拟教程：从入门到进阶分析](https://wenku.csdn.net/doc/845t0u7fv4?spm=1055.2635.3001.10343)
# 1. 长程作用力的物理基础和计算意义

在物理学中，长程作用力是指在空间上可传递无限远距离的力，常见的长程作用力包括库仑力和范德华力。在计算化学和分子模拟领域，长程作用力的精确计算对理解物质的性质和反应机理至关重要。这些力不仅是物质相互作用的基础，而且在分子动力学模拟中扮演着核心角色，决定了模拟结果的准确性和可靠性。随着模拟技术的发展，对长程作用力的计算提出了更高的要求，从而推动了相关算法和软件的发展，以实现更快速、更精确的模拟。本章将探讨长程作用力的物理基础，并分析其在分子模拟中的计算意义，为后续深入探讨NAMD软件和模拟实践奠定理论基础。

# 2. NAMD软件和分子模拟基础

## 2.1 NAMD软件的介绍

### 2.1.1 NAMD的历史和发展

NAMD（NAnoscale Molecular Dynamics）是一款专门为生物分子模拟设计的并行分子动力学软件，由美国国家超级计算应用中心（NCSA）和伊利诺伊大学香槟分校的生物物理科学系共同开发。自1995年首次发布以来，NAMD已经成为生物分子模拟领域中不可或缺的工具。

NAMD在发展过程中，始终保持着对计算效率和模拟精确性的高度关注，同时优化代码以适应最新的超级计算机架构。其支持多种并行计算架构，如共享内存和分布式内存，以及GPU加速，使得在模拟大规模生物分子体系时，能够有效地利用计算资源。

NAMD通过不断增加新功能和优化算法，不断扩大其在生物物理、材料科学和药物设计等领域的应用范围。随着生物大分子结构的解析技术进步，NAMD的用户群体也随之增加，成为科研人员不可或缺的模拟工具。

### 2.1.2 NAMD的主要功能和特点

NAMD的主要特点包括：

- **高性能**：NAMD能够利用超级计算机的并行处理能力，有效执行大规模的分子动力学模拟。
- **可扩展性**：它被设计成能够运行在从桌面工作站到大型超级计算机上，跨越多个计算平台。
- **多种力场支持**：NAMD支持多种常见的生物分子力场，如AMBER、CHARMM和OPLS-AA等。
- **算法创新**：它引入了多项创新算法来提高模拟的稳定性和精确性，如多重时间步长积分和非键合力的分步求和方法。
- **GPU加速**：NAMD支持NVIDIA CUDA架构的GPU加速，显著提升了计算速度。
- **可视化与分析工具**：NAMD与可视化工具VMD（Visual Molecular Dynamics）紧密集成，为用户提供了一站式的模拟与分析解决方案。

此外，NAMD还支持多尺度模拟，可以与量子力学程序如QM/MM方法结合使用，为用户提供更全面的研究手段。其丰富的文档和社区支持也是其受欢迎的原因之一。

## 2.2 分子动力学模拟的理论基础

### 2.2.1 动力学模拟的基本原理

分子动力学（Molecular Dynamics, MD）模拟是通过数值求解牛顿运动方程来追踪分子在时间上的运动。其核心步骤包括初始化系统状态、设置边界条件、应用力场计算原子间的相互作用力，然后通过积分器更新原子的位置和速度。

在模拟开始之前，通常需要设置系统的初始状态，这可能包括原子的位置、速度、温度、压力等参数。边界条件定义了系统与外界的相互作用，常见的边界条件有周期性边界条件和固定边界条件。周期性边界条件允许模拟在一个小的"单元盒"内，而视其为无限大的系统，这对于模拟液体和溶液中的分子特别有用。

力场是分子动力学模拟中的核心，它定义了原子之间相互作用的势能函数和力的计算方法。常见的力场参数包括键合相互作用（键长、键角和二面角势能）和非键相互作用（库仑力和范德华力）。

### 2.2.2 长程作用力在模拟中的角色

长程作用力在分子动力学模拟中扮演着关键角色，尤其是在模拟大分子系统时。这些力，如库仑力和范德华力，能够超越近距离的原子相互作用，影响整个分子系统的稳定性和动态行为。

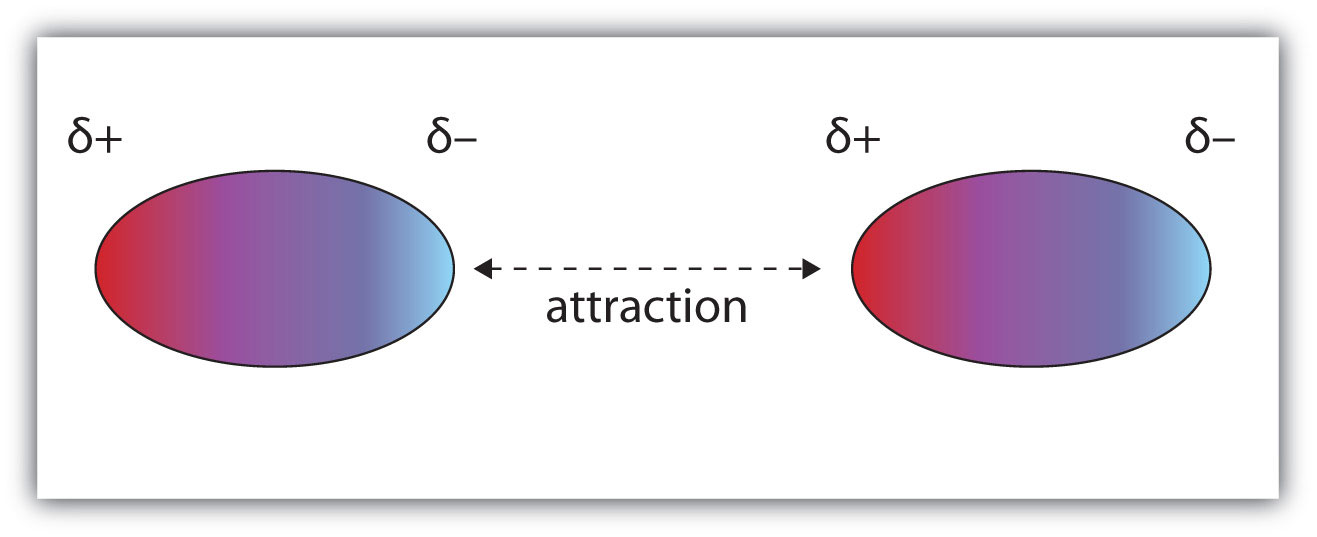
库仑力描述了带电原子或分子之间的电荷相互作用，而范德华力则描述了不带电原子或分子间的色散相互作用。这两个力的精确计算对于得到可靠的模拟结果至关重要。

为了在模拟中准确计算长程作用力，通常采用一些特殊技术来处理这些力。例如，力的截断和长程校正方法可以减少计算量，同时尽量避免由于截断带来的系统误差。

## 2.3 模拟中的力场和势能函数

### 2.3.1 力场的分类和选择

在分子动力学模拟中，力场扮演着至关重要的角色。力场是一种数学模型，它描述了原子或分子之间相互作用的势能函数。根据模拟目的和对象的不同，研究人员可以选择不同类型的力场。

- **经典力场**：如AMBER、CHARMM和OPLS-AA是广泛使用的经典力场，它们通过经验公式来描述原子之间的势能关系。
- **反应力场**：在化学反应过程中，力场需要能够描述键的断裂和形成，反应力场如ReaxFF能够实现这一功能。
- **量子力场**：对于需要精确描述电子效应的系统，量子力场如SCF/MM模型可以提供更高精度的模拟。

选择合适的力场对于获得可靠的模拟结果至关重要。力场的选择通常取决于模拟的分子类型和研究目的。比如，研究蛋白质结构时，AMBER和CHARMM力场因其参数化蛋白质的广泛研究而被普遍使用。

### 2.3.2 势能函数的表达式和计算方法

势能函数是力场的核心组成部分，它表达了系统内原子间的相互作用能。势能函数通常可以分为键合相互作用和非键相互作用两大类。

- **键合相互作用**：涉及键长、键角和二面角的相互作用。这些相互作用通常使用谐振子模型来描述。
\[ V_{bond}(r) = K_{bond} \left(r - r_0\right)^2 \]
其中，\( V_{bond} \)是键合势能，\( r \)是当前的键长，\( r_0 \)是平衡键长，\( K_{bond} \)是力常数。
- **非键相互作用**：包括范德华作用力和库仑力。范德华作用力通常用Lennard-Jones势来描述：

\[ V_{LJ}(r) = 4 \epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right] \]

其中，\( \epsilon \)是势井深度，\( \sigma \)是原子间平衡距离，\( r \)是原子间的距离。