堆的应用之十：最小生成树算法

# 3.1 堆的数据结构和操作

### 3.1.1 堆的定义和基本操作

堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。堆有两种类型：最小堆和最大堆。在最小堆中，根节点是堆中最小的元素，而在最大堆中，根节点是堆中最大的元素。

堆的基本操作包括：

* **插入：**将一个新元素插入堆中，保持堆的性质。
* **删除：**从堆中删除根节点，并重新排列堆以保持堆的性质。
* **查找：**在堆中查找一个元素。
* **更新：**更新堆中一个元素的值，并重新排列堆以保持堆的性质。

# 2. 最小生成树算法理论基础

### 2.1 最小生成树的概念和性质

**概念：**
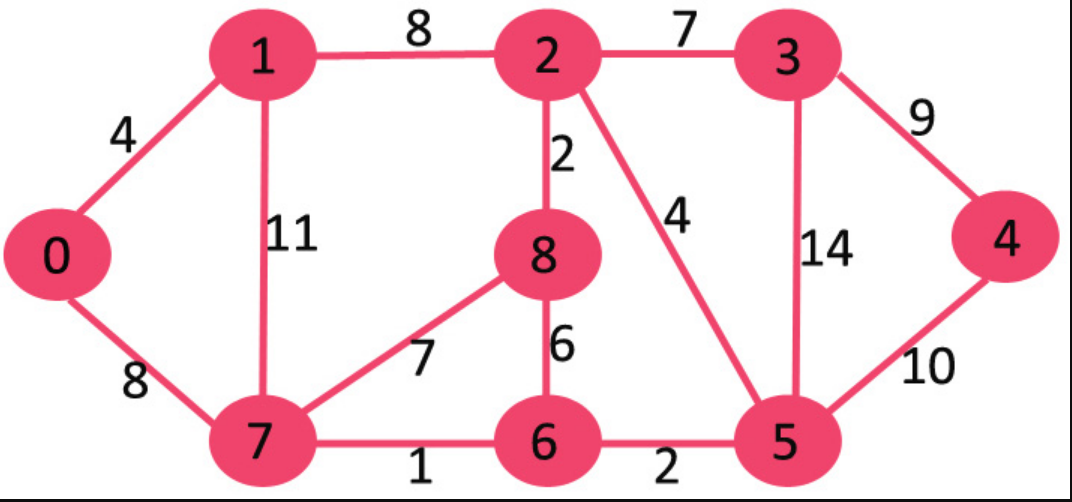
最小生成树（MST）是在给定的加权无向连通图中，连接所有顶点的边权和最小的生成树。

**性质：**
- **唯一性：**对于给定的加权无向连通图，只有一个最小生成树。
- **连通性：**MST连接图中的所有顶点。
- **无环：**MST中不存在环路。
- **最小权重：**MST中所有边的权重之和最小。

### 2.2 Prim算法和Kruskal算法

#### 2.2.1 Prim算法的原理和步骤

**原理：**
Prim算法从一个顶点开始，逐步添加权重最小的边，直到所有顶点都被连接。

**步骤：**
1. 选择一个顶点作为起点，并将其加入MST。
2. 对于当前MST中的每个顶点，找到连接到MST外部且权重最小的边。
3. 如果该边不存在，则算法结束。
4. 否则，将该边添加到MST，并将其连接的顶点加入MST。
5. 重复步骤2-4，直到所有顶点都被加入MST。

#### 2.2.2 Kruskal算法的原理和步骤

**原理：**
Kruskal算法将图中的所有边按权重从小到大排序，然后依次将这些边添加到MST中，直到所有顶点都被连接。

**步骤：**
1. 将图中的所有边按权重从小到大排序。
2. 初始化一个空MST。
3. 对于排序后的每条边：
- 如果该边不会形成环路，则将其添加到MST。
- 否则，丢弃该边。
4. 重复步骤3，直到所有顶点都被加入MST。

### 2.3 最小生成树的实际应用

最小生成树算法在实际应用中非常广泛，包括：

- **网络拓扑优化：**设计网络拓扑时，使用MST可以最小化网络的总线缆长度。
- **数据聚类：**使用MST可以将数据点聚类成不同的组，每个组内的点彼此相似度较高。
- **图像分割：**使用MST可以将图像分割成不同的区域，每个区域具有相似的颜色或纹理。

# 3. 最小生成树算法实现

### 3.1 堆的数据结构和操作

#### 3.1.1 堆的定义和基本操作

堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。堆通常用于实现优先队列，其中优先级最高的元素存储在根节点中。

堆的基本操作包括：

* **插入**：将一个新元素插入堆中，保持堆的性质。
* **删除**：从堆中删除根节点，并保持堆的性质。
* **查找最小值**：返回堆中最小值的根节点。

#### 3.1.2 堆的实现方式

堆可以通过数组或链表实现。数组实现更简单，而链表实现更灵活。

**数组实现**：

class Heap:
    def __init__(self):
        self.heap = []

    def insert(self, value):
        self.heap.append(value)
        self._heapify_up(len(self.heap) - 1)

    def delete(self):
        if len(self.heap) == 0:
            return None
        root = self.heap[0]
        self.heap[0] = self.heap[-1]
        self.heap.pop()
        self._heapify_down(0)
        return root

    def find_min(self):
        if len(self.heap) == 0:
            return None
        return self.heap[0]

    def _heapify_up(self, index):
        while index > 0:
            parent = (index - 1) // 2
            if self.heap[index] < self.heap[parent]:
                self.heap[index], self.heap[parent] = self.heap[parent], self.heap[index]
            index = parent

    def _heapify_down(self, index):
        while True:
            left = 2 * index + 1
            right = 2 * index + 2
            smallest = index
            if left < len(self.heap) and self.heap[left] < self.heap[smallest]:
                smallest = left
            if right < len(self.heap) and self.heap[right] < self.heap[smallest]:
                smallest = right
            if smallest == index:
                break
            self.heap[index], self.heap[smallest] = self.heap[smallest], self.heap[index]