堆与哈希表的结合应用

# 1. 堆与哈希表的理论基础**

堆和哈希表是两种基本的数据结构，在计算机科学中广泛应用。

* **堆**是一种基于完全二叉树实现的优先级队列，具有快速插入和删除最大/最小元素的特性。
* **哈希表**是一种基于哈希函数的数组，用于快速查找和插入数据，具有平均 O(1) 的时间复杂度。

# 2. 堆与哈希表结合应用的实践技巧

### 2.1 堆与哈希表结合的优势和适用场景

#### 2.1.1 性能优化

堆与哈希表结合可以显著提升数据处理的性能：

- **快速查找：**哈希表具有 O(1) 的平均查找时间，可快速定位特定元素。
- **高效插入和删除：**堆支持 O(log n) 的插入和删除操作，保持数据的有序性。

#### 2.1.2 数据结构互补

堆和哈希表具有互补的数据结构特性：

- **堆：**维护有序数据，支持高效的优先级队列操作。
- **哈希表：**基于键值对存储数据，提供快速的查找和插入。

结合使用时，可以利用堆的优先级队列特性处理有序数据，同时利用哈希表的快速查找和插入特性优化数据访问。

### 2.2 结合应用的实现方法

#### 2.2.1 哈希表作为堆的索引

- **原理：**哈希表存储堆中元素的键，指向堆中实际元素的位置。
- **优势：**快速查找堆中元素，时间复杂度为 O(1)。
- **代码示例：**

class IndexedHeap:
    def __init__(self):
        self.heap = []
        self.index = {}

    def insert(self, key, value):
        self.heap.append(value)
        self.index[key] = len(self.heap) - 1

    def find(self, key):
        if key in self.index:
            return self.heap[self.index[key]]
        return None

#### 2.2.2 堆作为哈希表的辅助结构

- **原理：**堆存储哈希表中元素的优先级，用于快速查找最大或最小元素。
- **优势：**高效获取哈希表中优先级最高的元素，时间复杂度为 O(log n)。
- **代码示例：**

class PriorityQueue:
    def __init__(self):
        self.hashtable = {}
        self.heap = []

    def insert(self, key, value):
        self.hashtable[key] = value
        self.heap.append(key)

    def find_max(self):
        if len(self.heap) == 0:
            return None
        max_key = self.heap[0]
        return self.hashtable[max_key]

### 2.3 常见问题及解决方式

#### 2.3.1 哈希冲突的处理

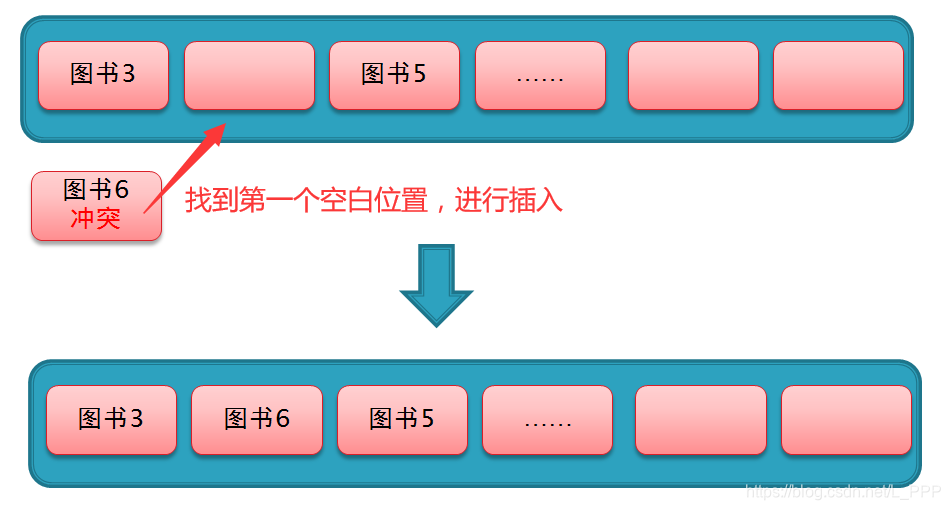
当哈希表中发生哈希冲突时，可以采用以下策略：

- **开放寻址法：**在哈希表中找到一个空闲位置插入元素。
- **链地址法：**使用链表将冲突的元素链接在一起。
- **二次探测法：**根据哈希函数的输出值，按照一定规则探测哈希表中的位置。

#### 2.3.2 堆的维护和优化

堆需要不断维护其有序性，可以采用以下优化措施：

- **堆化：**将无序数组转换为堆的数据结构。
- **上浮和下沉：**插入或删除元素时，通过比较与父节点或子节点的大小进行调整。
- **平衡因子：**引入平衡因子来衡量堆的平衡程度，并进行必要的旋转操作。

# 3.1 优先级队列的实现

#### 3.1.1 基于堆的优先级队列

基于堆的优先级队列利用堆的数据结构特性，将优先级最高的元素存储在堆的根节点上。当需要获取优先级最高的元素时，直接从根节点获取即可。

**实现方法：**

1. 使用最小堆或最大堆的数据结构。
2. 将元素按其优先级插入堆中。
3. 当需要获取优先级最高的元素时，从根节点获取并将其删除。

**代码示例：**

class MinHeapPriorityQueue:
    def __init__(self):
        self.heap = []

    def insert(self, element, priority):