快速排序测试与验证：确保算法正确性与性能的高级方法

# 1. 快速排序算法概述

快速排序是一种高效的排序算法，它采用分治策略，将一个数组分为两个子数组，其中一个子数组的元素都比另一个子数组的元素小，然后递归地排序两个子数组。

快速排序的基本思想是：选择一个基准值（pivot），然后将数组中的元素与基准值进行比较，并将元素重新排列成两个子数组，一个包含所有小于基准值的元素，另一个包含所有大于基准值的元素。然后，对这两个子数组递归地进行快速排序。

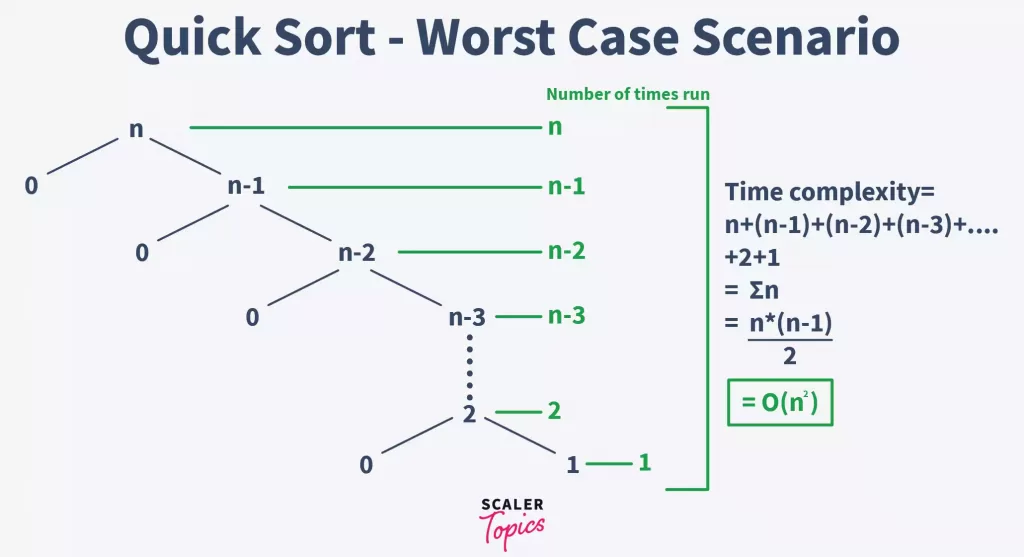
快速排序的平均时间复杂度为O(nlogn)，在大多数情况下，它的性能都优于其他排序算法。然而，在最坏情况下，其时间复杂度会退化为O(n^2)。因此，快速排序的优化和正确性验证是非常重要的。

# 2. 快速排序的理论基础

快速排序是计算机科学中一个非常重要的排序算法，它的基本思想是分治法。理解快速排序的理论基础，是掌握快速排序算法的关键所在。本章将从算法原理与流程、快速排序的变体两个方面，深入探讨快速排序的理论基础。

## 2.1 算法原理与流程

### 2.1.1 分治策略简介

分治策略是快速排序的核心策略，其基本思想是将一个难以直接解决的大问题分割成若干个小问题，各个击破，最终得到问题的解。在快速排序中，分治策略主要体现在将原始数组划分为较小的数组（两个子数组），然后递归排序两个子数组。

分治策略的应用可以分为三个步骤：
1. **分解**：将数组分解为若干子数组，每个子数组的规模尽量保持平衡。
2. **解决**：递归地解决子问题，如果子数组足够小，则直接排序。
3. **合并**：将各个子数组的排序结果合并为最终排序结果。

### 2.1.2 快速排序的基本步骤

快速排序的基本步骤可以用如下流程表示：

1. **选择基准值**：从数组中选择一个元素作为基准值（pivot），用于后续的分组依据。
2. **划分数组**：重新排列数组，将所有小于基准值的元素移到基准值的左边，将所有大于基准值的元素移到基准值的右边。这个过程结束时，基准值在其最终位置。
3. **递归排序子数组**：递归地将小于基准值的子数组和大于基准值的子数组排序。
4. **结束条件**：当子数组的大小为 0 或 1，该子数组已经有序，递归结束。

## 2.2 快速排序的变体

快速排序有许多变体，优化了原始算法的不同方面，如减少所需时间、节省空间、提高并行效率等。

### 2.2.1 三数取中法

在选择基准值时，原始方法通常选择第一个元素或随机选择一个元素。然而，这种选择可能导致效率低下，特别是在最坏情况下。**三数取中法**是一种优化策略，它选择三个元素的中位数作为基准值。

// C语言示例代码
int medianOfThree(int arr[], int left, int right) {
    int center = (left + right) / 2;
    if (arr[left] > arr[center])
        swap(&arr[left], &arr[center]);
    if (arr[left] > arr[right])
        swap(&arr[left], &arr[right]);
    if (arr[center] > arr[right])
        swap(&arr[center], &arr[right]);
    // 将基准值放到right-1的位置
    swap(&arr[center], &arr[right-1]);
    return arr[right-1];
}

这种策略减少了原始数组接近有序时可能导致的最坏情况。

### 2.2.2 尾递归优化

在某些语言中，如C语言，函数调用的栈空间是有限的，大量的递归可能导致栈溢出。**尾递归优化**是将快速排序的递归调用改写为尾递归形式，以减少栈空间的使用。

// C语言尾递归示例代码
void quicksortTailRecursive(int arr[], int low, int high) {
    while (low < high) {
        // 同样的分区步骤
        // ...

        if (low < high - 1) {
            quicksortTailRecursive(arr, low, high - 1);
            low++;
        } else {
            quicksortTailRecursive(arr, low + 1, high);
        }
    }
}

尾递归版本的快速排序保证了每个递归只会在栈上占用常数级的空间，而非线性级。

### 2.2.3 非递归实现

除了尾递归优化之外，快速排序还可以通过显式的栈数据结构来实现非递归算法。这种方法通过手动管理一个栈来跟踪要排序的子数组，从而避免了递归可能引起的问题。

// C语言非递归实现示例代码
void quicksortNonRecursive(int arr[], int left, int right) {
    stack<Interval> stack;
    stack.push(make_pair(left, right));

    while (!stack.empty()) {
        int low = ***().first;
        int high = ***().second;
        stack.pop();

        // 执行分区操作并获取pivot的新位置
        int pivot = partition(arr, low, high);

        if (pivot-1 > low) {
            stack.push(make_pair(low, pivot-1));
        }
        if (pivot+1 < high) {
            stack.push(make_pair(pivot+1, high));
        }
    }
}

通过使用显式栈，我们可以确保算法不会因为递归深度限制而失败，从而让算法变得更加健壮。

本章介绍了快速排序的理论基础，包括其基本原理、分治策略、以及如何通过不同变体改进原始算法的性能。理解这些概念对于深入应用和优化快速排序至关重要。在下一章，我们将探讨如何通过测试来验证快速排序的正确性。

# 3. 快速排序的正确性验证

## 3.1 正确性测试的重要性

### 3.1.1 编写测试用例的策略

在软件开发中，正确性验证是确保程序行为符合预期的基础环节。对于快速排序算法而言，由于其复杂性，编写一套全面且有效的测试用例显得尤为重要。测试用例的设计需要覆盖算法的各个方面，包括但不限于正常情况、边界条件以及异常情况。

策略一：结构化测试用例设计。可以将测试用例分为三大类：等价类划分、边界值分析和错误猜测。等价类划分指的是将输入数据的域分成若干个等价类，每个等价类中的数据可以互换，然后从每个等价类中选取少量代表作为测试用