快速排序适应性改进：针对有序数据集的优化策略

# 1. 快速排序算法概述

快速排序是一种高效的排序算法，由C.A.R. Hoare在1960年提出。它通过一个划分操作将数据分割成独立的两部分，其中一部分的所有数据都比另一部分的所有数据要小，然后再递归地对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序的基本步骤是：
1. 选择一个基准元素。
2. 将数组中小于基准的元素放在基准的左边，大于基准的放在右边。
3. 递归地对左右两部分继续进行排序。

此算法被广泛认为是排序算法中的“瑞士军刀”，在实际应用中，它的平均时间复杂度为O(n log n)，在大多数情况下都非常高效。然而，快速排序的性能在很大程度上依赖于基准元素的选择，而基准选择的不同策略也将是后续章节讨论的焦点。

# 2. 快速排序的基础理论

### 2.1 快速排序原理

#### 2.1.1 分区操作的详细步骤

快速排序的核心在于分区（Partitioning）操作，它将数据分为两部分，其中一部分的所有数据都比另一部分的所有数据要小。在分区过程中，选择一个基准值（Pivot），通常是最左边的元素、最右边的元素或者是一个随机元素。接下来，将数组中小于基准值的元素移动到基准值的左边，大于基准值的元素移动到基准值的右边。这个过程会进行直到所有的元素都被适当排列。

例如，考虑以下数组：

[5, 2, 9, 1, 5, 6]

我们选择最左边的元素5作为基准值，然后执行分区操作。分区后得到：

[1, 2, 5, 5, 9, 6]

左边是小于5的元素，右边是大于5的元素，其中5已经位于最终排序后的位置。

分区操作通常使用双指针方法，一个指针从左向右扫描，另一个指针从右向左扫描，通过交换指针位置的元素来确保左边都是小于等于基准值的元素，右边都是大于基准值的元素。

#### 2.1.2 快速排序的递归性质

快速排序是一个递归算法，其递归性质体现在将数组分成较小的部分后再分别对这些部分进行排序。排序的过程如下：

1. **分区操作**：如上所述，将数组分为两部分。
2. **递归排序**：对基准值左边的子数组和右边的子数组分别进行快速排序。
3. **组合结果**：将排序后的子数组与基准值合并，形成一个有序的数组。

递归过程继续直到所有子数组都只包含一个元素，此时数组就已经完全排序。递归的终止条件就是子数组不能再分割。

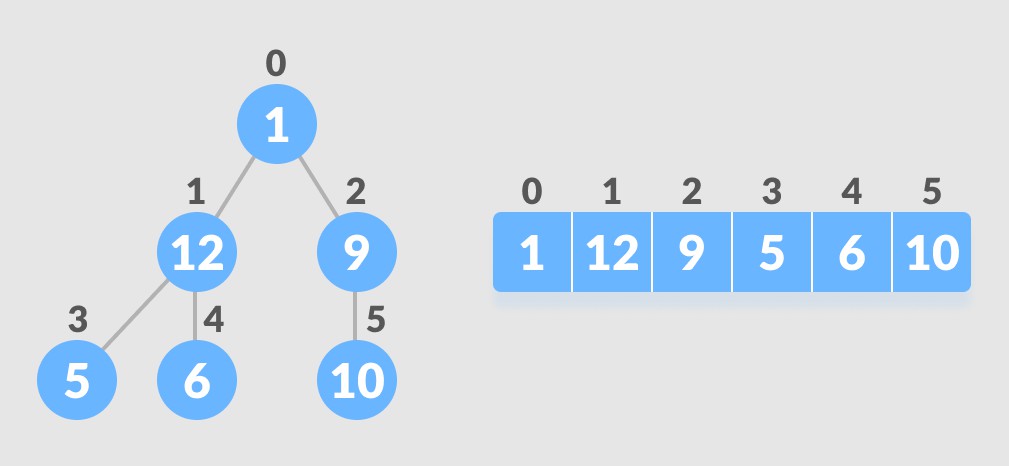
快速排序的递归过程可以通过递归树来形象地理解，每个节点代表一个递归调用，它将数组分成两部分，并递归地对这两部分进行排序。

### 2.2 快速排序的时间复杂度分析

#### 2.2.1 最优、平均和最差情况

快速排序的最优时间复杂度为O(n log n)，当每次分区都能将数组分成两个几乎相等的部分时达到，这种情况比较理想，但不容易在实际中遇到。

平均时间复杂度也是O(n log n)，这是在随机情况下分区操作分布比较均匀时的预期表现。

最差情况下的时间复杂度是O(n^2)，这种情况发生在每次分区只将数组分成两个极端不均匀的部分，例如，当数组已经是有序的情况下，每次选择的基准值都是最大或最小的元素。

#### 2.2.2 比较次数和交换次数的理论分析

快速排序的性能不仅仅与时间复杂度有关，还与比较次数和交换次数有关。比较次数是分区操作中对元素进行比较的次数，而交换次数是将元素移动到其最终位置的次数。

在平均情况下，快速排序大约进行`n log n`次比较，这是因为每次分区操作将数组分成两部分，然后在每一层递归中进行大约`n`次比较。交换次数通常少于比较次数，因为只有在两个元素的顺序错误时才会发生交换。

然而，在最差情况下，比较次数依然是O(n^2)，因为分区操作退化成线性时间复杂度。为了避免这种情况，通常在实际应用中采用各种优化技术，如随机选择基准值、使用三数取中法等。

以下是针对快速排序基础理论的Mermaid流程图示例，展示了快速排序的主要步骤：

graph TD;
    A[开始排序] --> B{选择基准值};
    B --> C[对数组进行分区];
    C --> D{基准值左侧是否有序};
    D -- 是 --> E[基准值右侧递归排序];
    D -- 否 --> C;
    E --> F{基准值右侧是否有序};
    F -- 是 --> G[结束排序];
    F -- 否 --> C;

代码块如下所示，展示了一个简单的快速排序算法实现，包括分区操作和递归过程：

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        less = [x for x in arr[1:] if x <= pivot]
        greater = [x for x in arr[1:] if x > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)

arr = [5, 2, 9, 1, 5, 6]
sorted_arr = quicksort(arr)
print(sorted_arr)

逻辑分析和参数说明：

1. 该代码片段定义了一个名为`quicksort`的函数，它接受一个数组`arr`作为参数。
2. 函数首先检查数组的长度，如果数组长度小于等于1，那么它已经有序，直接返回。
3. 否则，选择数组的第一个元素作为基准值`pivot`，并根据基准值将数组分为`less`和`greater`两个子数组。
4. 其中，`less`数组包含小于等于基准值的元素，而`greater`数组包含大于基准值的元素。
5. 最后，函数递归地对`less`和`greater`数组进行排序，并将结果连接起来，基准值`pivot`位于中间，返回最终的排序数组。

代码块通过递归地调用`quicksort`函数实现快速排序，使用了列表推导式来简化分区过程。注意，这个简单的实现可能不是最优化的版本，它没有考虑性能退化问题。

# 3. 针对有序数据集的排序优化

在前一章节中，我们深入探讨了快速排序算法的基础理论和性能分析。接下来，我们将关注点放在有序数据集上，这是因为有序数据集对快速排序的性能有着显著影响。我们将分析有序数据集带来的性能退化问题，并探讨避免这种性能退化的策略。此外，本章还将介绍改进的快速排序算法，包括三数取中法优化、非递归实现和尾递归优化以及栈模拟递归和迭代分割。

## 3.1 有序数据