GPU加速快速排序：硬件加速技术提升排序速度

# 1. GPU加速快速排序的基础知识

快速排序是一种高效的排序算法，但其在CPU上的单线程执行受限于冯·诺依曼架构的瓶颈。利用GPU（图形处理器）的并行处理能力来加速快速排序算法，可以在大数据集上取得显著的速度提升。GPU通过执行大量轻量级的线程来并行处理数据，这为快速排序算法提供了一个新的优化方向。GPU的并行计算优势，在处理数据量巨大的排序任务时尤其明显。然而，设计GPU友好的快速排序算法需要考虑线程同步、内存访问模式和带宽优化等挑战。本章将简要介绍快速排序的算法原理，并探讨GPU加速的基础概念，为后续章节深入分析和实践开发打下基础。

# 2. GPU加速技术的理论基础

## 2.1 GPU硬件架构及其加速原理

### 2.1.1 GPU的基本构成与工作原理
GPU（Graphics Processing Unit）最初是为图形和图像处理设计的专用处理器，但其高度并行的计算能力也使其成为大规模数值计算的理想选择。GPU的基本构成包括多个 Streaming Multiprocessors (SM)，每个 SM 包含多个 Streaming Processors (SP)，以及共享内存、常量内存等。这些组件共同协作，实现对大量数据的并行处理。

工作原理上，GPU通过将数据划分为小块（称为线程块或工作组），并分配给不同的 SM 处理。每个 SM 可以同时处理多个线程块中的线程，通过这种精细的数据并行性和线程并行性，GPU能够处理比CPU更复杂的数据集合。

### 2.1.2 GPU并行处理的优势与限制
GPU并行处理的优势主要体现在处理大规模、高度并行的计算任务时的高效率。相较于CPU，GPU拥有更多的核心和更高的内存带宽，这意味着在处理并行算法时，如矩阵运算、图像渲染和深度学习计算，它能够提供显著的性能提升。

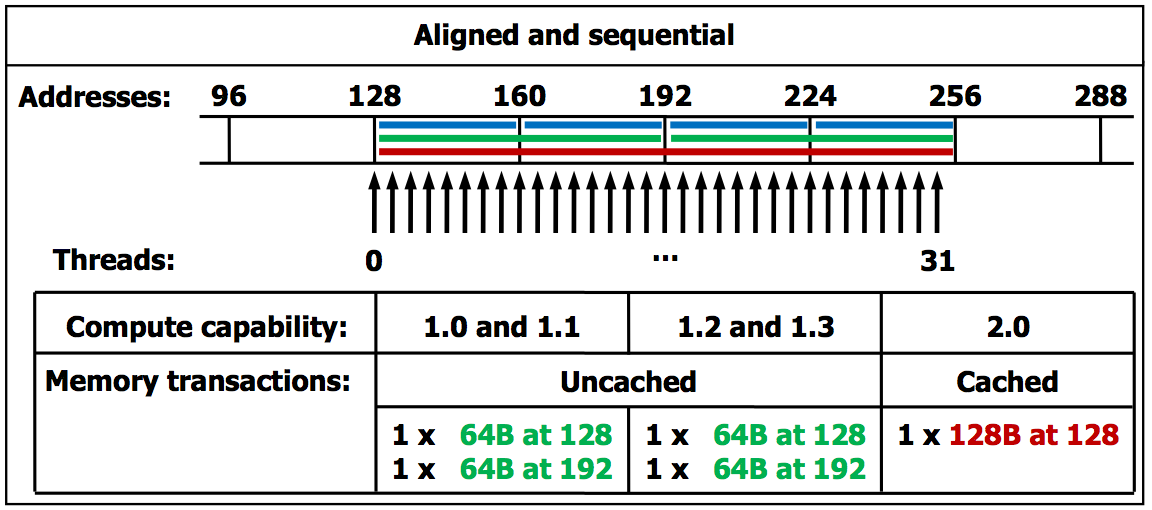
然而，GPU的并行架构也带来了一些限制。首先是内存访问模式的限制，GPU对内存访问模式有更严格的要求，非对齐或非连续的内存访问会导致性能下降。其次，GPU编程模型要求程序员对并行化和内存管理有更深入的理解，这对于某些算法的实现可能会增加难度。

## 2.2 GPU编程模型与API概述

### 2.2.1 CUDA编程模型简介
CUDA（Compute Unified Device Architecture）是NVIDIA推出的一种并行计算平台和编程模型，它允许开发者直接使用NVIDIA的GPU进行通用计算。CUDA模型中，程序员可以定义 Kernel 函数，这些函数在GPU上的成百上千个线程上并发执行。CUDA提供了丰富的内存层次结构，包括全局内存、共享内存、常量内存和纹理内存等。

CUDA的编程模型简单而强大，只需要在C/C++代码中添加特定的语句和关键字，就可以在GPU上运行代码。此外，CUDA还提供了一整套的工具和库，如cuBLAS、cuFFT、NPP等，用于加速数学运算、图像处理等特定类型的应用。

### 2.2.2 OpenCL与Vulkan Compute的比较
OpenCL（Open Computing Language）和Vulkan Compute是两个与CUDA竞争的开放标准编程接口，它们允许在多种平台上实现并行计算。

OpenCL是一种更开放和标准的异构编程环境，它支持多种类型的处理器，包括CPU、GPU和DSP。OpenCL编程模型允许开发者编写可以在多个硬件平台上运行的代码，但其编程复杂度高于CUDA，且性能优化较困难。

Vulkan Compute是Khronos组织推出的最新一代图形和计算API，旨在提供更低的CPU开销和更细粒度的控制。Vulkan Compute与Vulkan图形API紧密集成，可以实现高性能的图形和计算任务。Vulkan Compute的优势在于它能够更好地利用现代GPU的计算能力，但同样也面临着更复杂的开发环境。

## 2.3 排序算法的理论分析

### 2.3.1 快速排序算法的工作原理
快速排序是一种高效的排序算法，通过分治法的策略实现。它首先从数组中选择一个元素作为基准（pivot），然后重新排列数组，所有比基准小的元素摆放在基准前面，所有比基准大的元素摆放在基准后面。这个过程称为分区（partitioning）。递归地对基准前后的子数组进行快速排序，直到整个数组变为有序。

快速排序的平均时间复杂度为O(n log n)，但在最坏情况下（例如，当输入数组已经是有序的）时间复杂度会退化到O(n^2)。

### 2.3.2 排序算法的时间复杂度与空间复杂度
时间复杂度和空间复杂度是衡量排序算法性能的两个重要指标。对于快速排序来说，其最理想状态下的时间复杂度为O(n log n)，即每一轮分区后，待排序的数组大小减半，这样的时间复杂度下算法的运行时间随着输入数据量的增加而对数增长。

空间复杂度方面，快速排序是一个原地排序算法，除了递归调用栈之外，不需要额外的存储空间。因此，它的空间复杂度为O(log n)，主要由递归的深度决定，这在非递归实现或尾递归优化的情况下可以降低到O(1)。

然而，在实际应用中，快速排序可能需要额外的空间来处理分区，特别是在处理具有大量重复元素的数据集时，可能会退化到O(n)。为了优化这一点，有多种快速排序的变种，如三数取中法、随机基准法等，可以在一定程度上减少对空间的需求。

# 3. GPU快速排序的实践开发

随着技术的发展和硬件能力的提升，GPU（图形处理单元）已成为实现并行计算的重要工具。在本章中，我们将深入探讨如何将快速排序算法应用于GPU以实现加速，并详细介绍开发环境的搭建、核心算法的GPU版本设计、数据传输与内存管理，以及性能优化与调试技巧。

## 3.1 环境搭建与基础框架

在开始GPU快速排序算法的实现之前，我们需要搭建开发环境并建立基础框架。开发环境的配置和基础框架的设计对于后续