动态规划：解决复杂问题的强大工具，掌握动态规划技巧

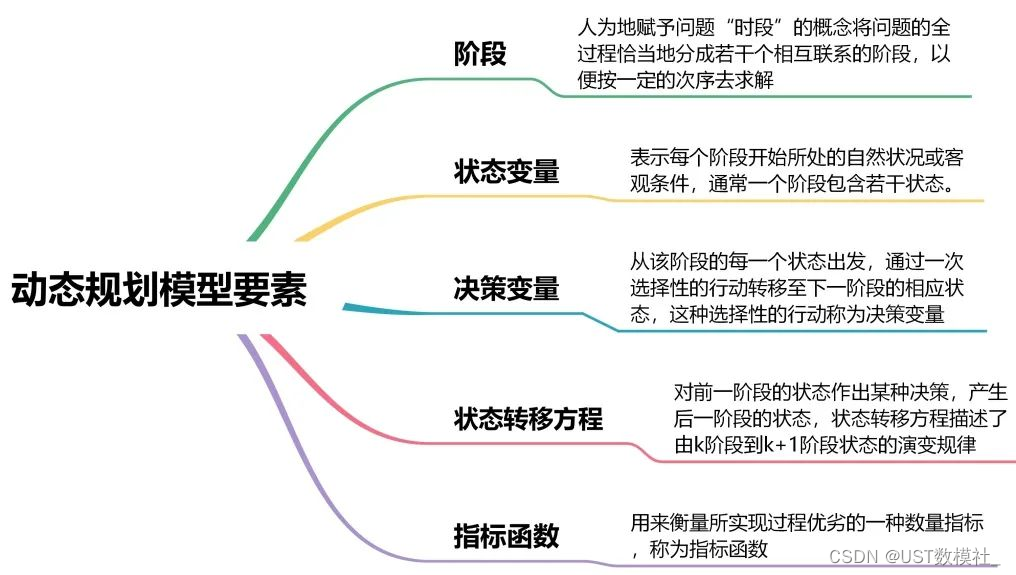
# 1. 动态规划概述**

动态规划是一种解决复杂问题的强大算法技术，它通过将问题分解成更小的子问题，并存储子问题的解决方案来逐步解决问题。动态规划算法的特点包括：

- **最优子结构：**问题的最优解包含其子问题的最优解。
- **重叠子问题：**子问题在问题的不同部分重复出现，导致不必要的重复计算。
- **无后效性：**子问题的解决方案不依赖于其求解顺序。

# 2. 动态规划的基本原理

### 2.1 动态规划的定义和特点

**定义：**

动态规划是一种解决复杂问题的算法范式，它将问题分解成更小的子问题，并通过逐步求解这些子问题来得到最终解。

**特点：**

* **最优子结构：**问题的最优解包含其子问题的最优解。
* **重叠子问题：**子问题在求解过程中可能被重复计算。
* **无后效性：**子问题的解与后续子问题的求解无关。

### 2.2 动态规划的步骤和思想

**步骤：**

1. **分解问题：**将问题分解成一系列相互关联的子问题。
2. **定义状态：**确定描述子问题状态的变量。
3. **建立状态转移方程：**描述如何从已知状态转移到新状态。
4. **初始化：**设置初始状态的值。
5. **计算：**按某种顺序依次计算所有状态的值。
6. **回溯：**从最终状态出发，通过状态转移方程回溯求得最优解。

**思想：**

动态规划的思想是将问题分解成子问题，并通过存储和重用子问题的解来避免重复计算。通过逐步求解子问题，最终得到整个问题的最优解。

**示例：**

考虑斐波那契数列的求解问题。斐波那契数列的第 `n` 项可以通过以下公式计算：

F(n) = F(n-1) + F(n-2)

使用动态规划求解该问题：

* **分解问题：**将求解 `F(n)` 问题分解成求解 `F(n-1)` 和 `F(n-2)` 的子问题。
* **定义状态：**状态为 `F(i)`，表示斐波那契数列的第 `i` 项。
* **建立状态转移方程：**`F(i) = F(i-1) + F(i-2)`。
* **初始化：**`F(0) = 0`，`F(1) = 1`。
* **计算：**按顺序计算 `F(2)`、`F(3)`、...，`F(n)`。
* **回溯：**从 `F(n)` 出发，通过状态转移方程回溯求得 `F(n-1)`、`F(n-2)`，...，`F(0)`。

# 3.1 背包问题

背包问题是动态规划中经典且重要的应用场景之一。它描述了一个场景：有一个背包，容量为 W，有 n 件物品，每件物品有自己的重量 wi 和价值 vi。目标是找出一种装载物品的方法，使得背包中的物品总重量不超过 W，并且总价值最大。

**问题形式化：**

def knapsack(W, wt, val, n):
    """
    背包问题：在背包容量限制下，选择物品最大化总价值

    参数：
        W: 背包容量
        wt: 物品重量列表
        val: 物品价值列表
        n: 物品数量
    """
    dp = [[0 for _ in range(W + 1)] for _ in range(n + 1)]

    for i in range(1, n + 1):
        for j in range(1, W + 1):
            if wt[i - 1] > j:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], val[i - 1] + dp[i - 1][j - wt[i - 1]])

    return dp[n][W]

**代码逻辑分析：**

1. 创建一个二维数组 `dp`，其中 `dp[i][j]` 表示前 `i` 件物品放入容量为 `j` 的背包中的最大价值。
2. 对于每件物品 `i`，遍历背包容量 `j` 的所有可能值。
3. 如果物品 `i` 的重量大于背包容量 `j`，则不考虑该物品，`dp[i][j]` 等于前一个物品 `i-1` 的最大价值 `dp[i-1][j]`.
4. 否则，考虑两种情况：
- 不放入物品 `i`，则最大价值为前一个物品 `i-1` 的最大价值 `dp[i-1][j]`。
- 放入物品 `i`，则最大价值为物品 `i` 的价值 `val[i-1]` 加上不放入物品 `i` 时前一个背包容量 `j-wt[i-1]` 的最大价值 `dp[i-1][j