【算法分析秘籍】：从基础到实战，解锁算法世界

# 1. 算法基础**

算法是计算机科学中用于解决问题的明确而详细的步骤集合。算法基础是算法领域的基石，为理解算法设计、分析和应用奠定基础。

算法的基本概念包括：

- **输入和输出：**算法接收输入并产生输出。
- **算法效率：**算法的效率由其时间复杂度（运行时间）和空间复杂度（内存使用）衡量。
- **算法正确性：**算法必须始终产生正确的输出，无论输入是什么。

# 2. 算法设计与分析**

**2.1 算法设计原则**

算法设计原则指导我们如何设计出高效、可维护的算法。本章节将介绍两种重要的算法设计原则：贪心算法和分治算法。

**2.1.1 贪心算法**

贪心算法是一种逐个做出局部最优选择的算法。它基于这样一个假设：在每个步骤中做出局部最优的选择，最终将导致全局最优解。贪心算法的优势在于其简单性和效率，但它并不总是能找到全局最优解。

**代码块 2.1：贪心算法示例（求解背包问题）**

def greedy_knapsack(items, capacity):
    """
    贪心算法求解背包问题

    参数：
        items: 物品列表，每个物品包含价值和重量
        capacity: 背包容量

    返回：
        背包中物品的最大总价值
    """
    # 根据价值/重量比对物品进行排序
    items.sort(key=lambda item: item.value / item.weight, reverse=True)

    # 逐个将物品放入背包，直到背包装满
    total_value = 0
    for item in items:
        if item.weight <= capacity:
            total_value += item.value
            capacity -= item.weight
        else:
            # 如果物品重量超过剩余容量，则按比例放入
            total_value += item.value * (capacity / item.weight)
            break

    return total_value

**逻辑分析：**

该代码块实现了贪心算法求解背包问题。背包问题是一个经典的优化问题，目标是将一组物品放入容量有限的背包中，使得背包中物品的总价值最大。贪心算法按照价值/重量比对物品进行排序，然后逐个将物品放入背包，直到背包装满。如果物品重量超过剩余容量，则按比例放入。

**2.1.2 分治算法**

分治算法是一种将问题分解成较小、更简单的子问题，然后递归地求解这些子问题的算法。分治算法的优势在于其效率和可并行性，但它可能需要额外的空间开销。

**代码块 2.2：分治算法示例（归并排序）**

def merge_sort(arr):
    """
    分治算法实现归并排序

    参数：
        arr: 待排序数组

    返回：
        排序后的数组
    """
    if len(arr) <= 1:
        return arr

    # 将数组分成两部分
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])

    # 合并两个排序后的子数组
    return merge(left_half, right_half)

def merge(left, right):
    """
    合并两个排序后的数组

    参数：
        left: 左侧排序后的数组
        right: 右侧排序后的数组

    返回：
        合并后的排序数组
    """
    i, j = 0, 0
    merged = []
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1

    # 将剩余元素添加到合并后的数组
    merged.extend(left[i:])
    merged.extend(right[j:])

    return merged

**逻辑分析：**

该代码块实现了分治算法实现归并排序。归并排序是一种稳定的排序算法，其时间复杂度为 O(n log n)。分治算法将数组分成两部分，然后递归地对这两部分进行排序。最后，将排序后的两部分合并成一个排序后的数组。

**2.2 算法分析方法**

算法分析方法用于评估算法的效率和性能。本章节将介绍两种重要的算法分析方法：时间复杂度分析和空间复杂度分析。

**2.2.1 时间复杂度分析**

时间复杂度分析衡量算法在最坏情况下执行所需的时间。它通常表示为 O(n)，其中 n 是输入大小。时间复杂度分析对于比较不同算法的效率至关重要。

**表格 2.1：常见的时间复杂度**

| 时间复杂度 | 描述 |
|---|---|
| O(1) | 常数时间 |
| O(log n) | 对数时间 |
| O(n) | 线性时间 |
| O(n log n) | 线性对数时间 |
| O(n^2) | 平方时间 |
| O(2^n) | 指数时间 |

**2.2.2 空间复杂度分析**

空间复杂度分析衡量算法在执行过程中所需的内存量。它通常表示为 O(n)，其中 n 是输入大小。空间复杂度分析对于评估算法在有限内存环境中的可行性至关重要。

**代码块 2.3：空间复杂度分析示例**

def factorial(n):
    """
    计算阶乘

    参数：
        n: 非负整数

    返回：
        n 的阶乘
    """
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

**逻辑分析：**

该代码块计算一个非负整数的阶乘。阶乘是一个递归算法，其空间复杂度为 O(n)，因为递归调用会在栈中创建 n 个函数调用帧。

# 3. 经典算法实战**

**3.1 排序算法**

排序算法是计算机科学中的一类基本算法，用于将一组元素按特定顺序排列。排序算法有多种，每种算法都有其自身的优点和缺点。本节将介绍两种经典的排序算法：冒泡排序和快速排序。

**3.1.1 冒泡排序**

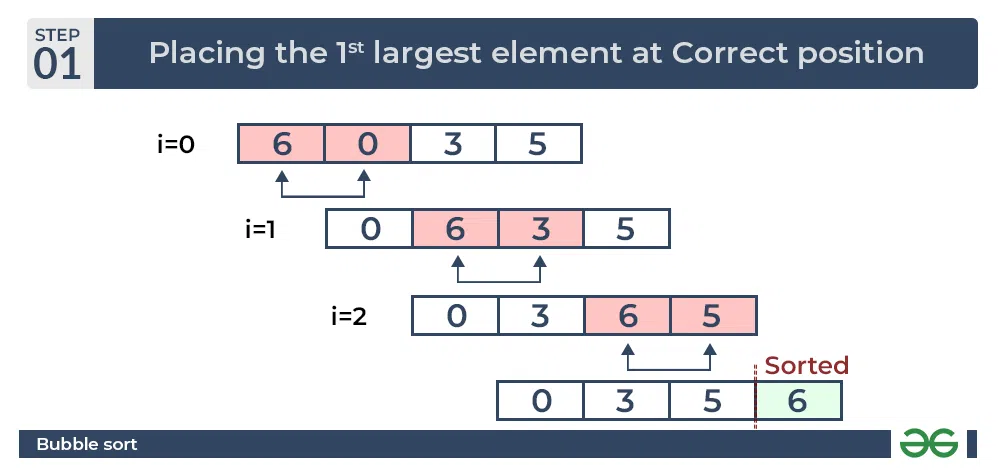
冒泡排序是一种简单直观的排序算法。其基本思想是将相邻的两个元素进行比较，如果顺序不正确，则交换这两个元素。重复这一过程，直到所有元素都按正确顺序排列。

def bubble_sort(arr):
    """冒泡排序算法

    Args:
        arr: 待排序的数组

    Returns:
        排序后的数组
    """
    for i in range(len(arr)):
        for j in range(len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

**逻辑分析：**

* 外层循环 `for i in range(len(arr))` 遍历数组元素。
* 内层循环 `for j in range(len(arr) - i - 1)` 比较相邻元素并交换。
* 每次外层循环结束，最大的元素会“浮”到数组末尾。

**时间复杂度：** O(n^2)，其中 n 为数组长度。

**空间复杂度：** O(1)，因为算法不使用额外的空间。

**3.1.2 快速排序**

快速排序是一种高效的排序算法，其基本思想是将数组划分为两个子数组，一个子数组包含比基准元素小的元素，另一个子数组包含比基准元素大的元素。然后递归地对两个子数组进行排序。

def quick_sort(arr, low, high):
    """快速排序算法

    Args:
        arr: 待排序的数组
        low: 数组的起始索引
        high: 数组的结束索引

    Returns:
        排序后的数组
    """
    if low < high:
        pivot = partition(arr, low, high)
        quick_sort(arr, low, pivot - 1)
        quick_sort(arr, pivot + 1, high)

def partition(arr, low, high):
    """划分数组

    Args:
        arr: 待排序的数组
        low: 数组的起始索引
        high: 数组的结束索引

    Returns:
        基准元素的索引
    """
    pivot = arr[high]
    i = low - 1
    for j in range(low, high):
        if arr[j] <= pivot:
            i += 1
            arr[i], arr[j] = arr[j], arr[i]
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    return i + 1

**逻辑分析：**

* `partition` 函数选择数组最后一个元素作为基准元素，并将其移动到正确的位置。
* 然后，`quick_sort` 函数递归地对基准元素左侧和右侧的子数组进行排序。
* 这种算法通过将数组划分为较小的子数组来提高效率。

**时间复杂度：** 平均 O(n log n)，最坏情况 O(n^2)，其中 n 为数组长度。

**空间复杂度：** O(log n)，因为算法使用递归调用栈。

**3.2 搜索算法**

搜索算法是计算机科学中另一类基本算法，用于在数据结构中查找特定元素。搜索算法有多种，每种算法都有其自身的优点和缺点。本节将介绍两种经典的搜索算法：线性搜索和二分搜索。

**3.2.1 线性搜索**

线性搜索是一种简单直观的搜索算法。其基本思想是顺序遍历数据结构，并与目标元素进行比较。如果找到目标元素，则返回其位置；否则返回 -1。

def linear_search(arr, target):
    """线性搜索算法

    Args:
        arr: 待搜索的数组
        target: 目标元素

    Returns:
        目标元素的索引，如果未找到则返回 -1
    """
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

**逻辑分析：**

* 算法遍历数组中的每个元素，并将其与目标元素进行比较。
* 如果找到目标元素，则返回其索引。
* 如果未找到目标元素，则返回 -1。

**时间复杂度：** O(n)，其中 n 为数组长度。

**空间复杂度：** O(1)，因为算法不使用额外的空间。

**3.2.2 二分搜索**

二分搜索是一种高效的搜索算法，其基本思想是将数据结构划分为两半，并与目标元素进行比较。如果目标元素在前半部分，则递归地对前半部分进行搜索；否则，递归地对后半部分进行搜索。

def binary_search(arr, target, low, high):
    """二分搜索算法

    Args:
        arr: 待搜索的数组
        target: 目标元素
        low: 数组的起始索引
        high: 数组的结束索引

    Returns:
        目标元素的索引，如果未找到则返回 -1
    """
    if low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            return binary_search(arr, target, mid + 1, high)
        else:
            return binary_search(arr, target, low, mid - 1)
    return -1

**逻辑分析：**

* 算法将数组划分为两半，并与目标元素进行比较。
* 如果目标元素在前半部分，则递归地对前半部分进行搜索。
* 如果目标元素在后半部分，则递归地对后半部分进行搜索。
* 这种算法通过将搜索范围减半来提高效率。

**时间复杂度：** O(log n)，其中 n 为数组长度。

**空间复杂度：** O(1)，因为算法不使用额外的空间。

# 4. 算法优化与应用

### 4.1 算法优化技巧

#### 4.1.1 缓存和备忘录

**概念：**

缓存和备忘录是一种优化技术，用于存储先前计算的结果，以避免重复计算。缓存通常用于存储最近访问的数据，而备忘录则用于存储所有计算过的结果。

**工作原理：**

当需要计算某个值时，首先检查缓存或备忘录中是否已经存储了该值。如果已经存储，则直接返回该值，无需重新计算。否则，执行计算并将其结果存储在缓存或备忘录中，以备将来使用。

**优点：**

* 减少计算时间，提高性能。
* 避免重复计算，节省资源。
* 提高代码的可读性和可维护性。

**代码示例：**

# 缓存最近访问的数据
cache = {}

def get_value(key):
    if key in cache:
        return cache[key]
    else:
        value = calculate_value(key)
        cache[key] = value
        return value

# 备忘录存储所有计算过的结果
memo = {}

def fibonacci(n):
    if n in memo:
        return memo[n]
    else:
        if n <= 1:
            result = n
        else:
            result = fibonacci(n-1) + fibonacci(n-2)
        memo[n] = result
        return result

#### 4.1.2 并行化和分布式计算

**概念：**

并行化和分布式计算是一种优化技术，用于将计算任务分解成较小的子任务，并在多个处理器或计算机上同时执行。

**工作原理：**

* **并行化：**将任务分解成多个独立的子任务，并在同一台计算机上的多个处理器上同时执行。
* **分布式计算：**将任务分解成多个子任务，并在不同的计算机上同时执行。

**优点：**

* 大幅缩短计算时间。
* 充分利用多核处理器和分布式系统。
* 提高系统的吞吐量和可扩展性。

**代码示例：**

# 使用多线程并行化
import threading

def parallel_sum(numbers):
    num_threads = 4  # 4个线程
    chunk_size = len(numbers) // num_threads

    threads = []
    for i in range(num_threads):
        start = i * chunk_size
        end = (i + 1) * chunk_size
        thread = threading.Thread(target=sum_chunk, args=(numbers[start:end],))
        threads.append(thread)

    for thread in threads:
        thread.start()

    for thread in threads:
        thread.join()

    return sum(partial_sums)  # 汇总各个线程的局部和

# 使用分布式计算
import dask

def distributed_sum(numbers):
    dask_array = dask.array.from_array(numbers)
    result = dask_array.sum().compute()
    return result

### 4.2 算法在实际问题中的应用

#### 4.2.1 图论算法

**概念：**

图论算法用于解决与图结构相关的问题，例如路径查找、连通性分析和最小生成树等。

**应用场景：**

* 社交网络分析
* 交通网络优化
* 计算机图形学
* 数据挖掘

**代码示例：**

# 使用深度优先搜索查找路径
def dfs_path(graph, start, end):
    stack = [start]
    visited = set()

    while stack:
        node = stack.pop()
        if node == end:
            return True
        if node not in visited:
            visited.add(node)
            for neighbor in graph[node]:
                stack.append(neighbor)

    return False

# 使用克鲁斯卡尔算法计算最小生成树
def kruskal_mst(graph):
    edges = [(weight, u, v) for u, v, weight in graph.edges(data='weight')]
    edges.sort()

    parent = {node: node for node in graph.nodes()}
    rank = {node: 0 for node in graph.nodes()}

    def find(node):
        if parent[node] != node:
            parent[node] = find(parent[node])
        return parent[node]

    def union(u, v):
        root_u = find(u)
        root_v = find(v)
        if root_u != root_v:
            if rank[root_u] > rank[root_v]:
                parent[root_v] = root_u
            else:
                parent[root_u] = root_v
                if rank[root_u] == rank[root_v]:
                    rank[root_v] += 1

    mst = []
    for weight, u, v in edges:
        if find(u) != find(v):
            mst.append((u, v, weight))
            union(u, v)

    return mst

#### 4.2.2 数据挖掘算法

**概念：**

数据挖掘算法用于从大型数据集发现隐藏的模式、趋势和关联。

**应用场景：**

* 客户细分
* 市场预测
* 欺诈检测
* 推荐系统

**代码示例：**

# 使用 k-means 聚类算法
from sklearn.cluster import KMeans

def kmeans_clustering(data, k):
    model = KMeans(n_clusters=k)
    model.fit(data)

    return model.labels_

# 使用关联规则挖掘算法
from mlxtend.frequent_patterns import apriori, association_rules

def association_rule_mining(transactions, min_support=0.2, min_confidence=0.5):
    frequent_itemsets = apriori(transactions, min_support=min_support)
    rules = association_rules(frequent_itemsets, min_confidence=min_confidence)

    return rules

# 5.1 算法竞赛平台和资源

算法竞赛是提高算法能力和解决问题技巧的绝佳途径。参与算法竞赛不仅可以检验自己的算法水平，还可以与来自世界各地的算法高手交流学习。目前，主流的算法竞赛平台包括：

- **LeetCode**：提供海量的算法题目和讨论区，是算法竞赛入门和练习的理想平台。
- **Codeforces**：以其高质量的题目和激烈的比赛闻名，吸引了众多算法高手参与。
- **TopCoder**：历史悠久的算法竞赛平台，提供各种类型的竞赛和挑战。
- **HackerRank**：专注于解决现实世界问题的算法竞赛，题目涵盖广泛的领域。
- **Kaggle**：一个数据科学和机器学习竞赛平台，提供大量数据集和算法问题。

这些平台提供了丰富的学习资源，包括教程、讨论区和代码示例，帮助算法竞赛爱好者提升技能。

## 5.2 算法竞赛策略和技巧

算法竞赛中，除了扎实的算法基础，还需要掌握一些策略和技巧，才能在众多参赛者中脱颖而出。以下是一些常见的策略：

- **选择合适的题目**：根据自己的算法水平和时间安排，选择难度适中的题目。
- **快速阅读题目**：仔细阅读题目描述，理解题目要求和输入输出格式。
- **设计高效算法**：根据题目要求，选择合适的算法并优化其效率。
- **调试和测试**：编写代码后，仔细调试和测试，确保算法正确无误。
- **优化代码**：在保证算法正确性的前提下，尽可能优化代码，减少时间和空间复杂度。
- **利用社区资源**：积极参与讨论区，向高手请教，学习别人的解题思路。

## 5.3 算法研究与前沿探索

算法竞赛不仅是提高算法能力的途径，也是算法研究和前沿探索的窗口。通过参与算法竞赛，可以接触到最新算法和技术，并与算法领域的前沿研究者交流。

一些算法竞赛平台会举办专门的算法研究竞赛，鼓励参赛者提出新的算法或优化现有算法。此外，算法竞赛社区中也活跃着许多算法研究者，他们不断提出新的算法思想和优化技术。

参与算法竞赛和研究，不仅可以提升算法能力，还可以拓宽算法视野，为未来的算法研究和应用打下坚实的基础。