算法数据结构：理解算法背后的数据组织，提升算法效率

# 1. 算法与数据结构概述**

算法是解决特定问题的一系列步骤，而数据结构是组织和存储数据的方式。两者相互关联，算法依赖于数据结构来高效地处理数据，而数据结构的效率又影响着算法的性能。

数据结构的常见类型包括数组、链表、栈和队列，每种类型都有其独特的特性和应用场景。例如，数组适合存储固定大小的元素，链表适合存储动态大小的数据，栈和队列遵循先进先出（FIFO）和后进先出（LIFO）的原则。

# 2. 数据结构与算法效率

### 2.1 数组、链表、栈和队列

#### 2.1.1 数组的特性和应用场景

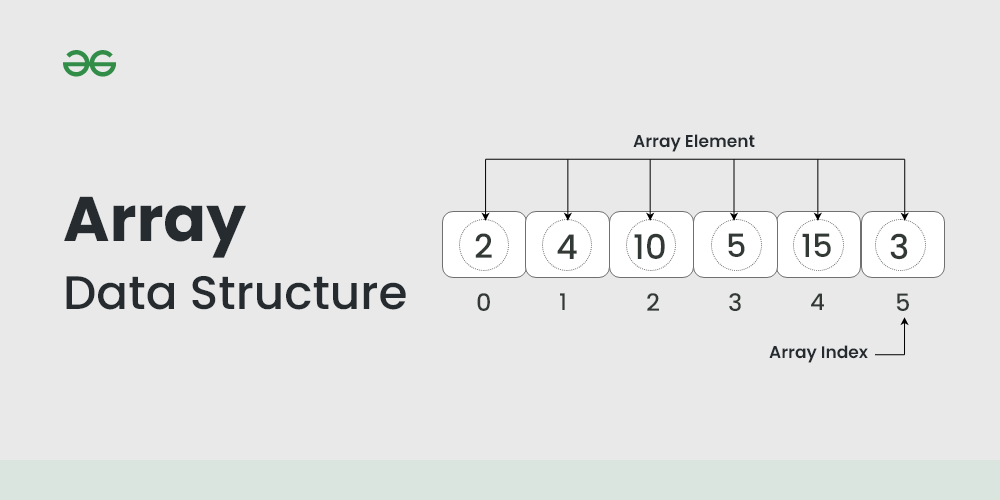
数组是一种线性数据结构，其元素存储在连续的内存位置中。数组的每个元素都有一个唯一的索引，可用于快速访问和修改。

**特性：**

- **顺序访问：**数组元素只能按顺序访问，从第一个元素到最后一个元素。
- **固定大小：**数组的大小在创建时确定，并且无法在运行时动态更改。
- **高效的随机访问：**使用索引可以快速访问数组中的任何元素。

**应用场景：**

- 存储大量需要顺序访问的数据，例如数字数组或字符数组。
- 作为其他数据结构的基础，例如链表和队列。

#### 2.1.2 链表的特性和应用场景

链表是一种线性数据结构，其元素存储在不连续的内存位置中。每个元素包含数据和指向下一个元素的指针。

**特性：**

- **动态大小：**链表的大小可以动态增长或缩小，无需预先分配内存。
- **插入和删除高效：**在链表中插入或删除元素只需要修改指针，而无需移动数据。
- **顺序访问效率低：**访问链表中的元素需要遍历整个链表，效率较低。

**应用场景：**

- 存储需要频繁插入和删除的数据，例如哈希表或栈。
- 作为其他数据结构的基础，例如二叉树或图。

#### 2.1.3 栈和队列的特性和应用场景

栈和队列都是线性数据结构，但它们具有不同的操作规则。

**栈：**

**特性：**

- **后进先出 (LIFO)：**元素只能从栈顶添加或删除。
- **高效的插入和删除：**在栈顶进行操作，无需遍历整个栈。

**应用场景：**

- 存储需要按相反顺序访问的数据，例如函数调用记录。
- 作为其他数据结构的基础，例如递归算法或括号匹配。

**队列：**

**特性：**

- **先进先出 (FIFO)：**元素只能从队列尾部添加，从队列头部删除。
- **高效的插入和删除：**在队列尾部或头部进行操作，无需遍历整个队列。

**应用场景：**

- 存储需要按顺序处理的数据，例如任务队列或消息队列。
- 作为其他数据结构的基础，例如广度优先搜索算法。

### 2.2 数据结构对算法效率的影响

数据结构的选择对算法的效率有重大影响。

#### 2.2.1 时间复杂度分析

时间复杂度衡量算法执行所需的时间。它通常表示为大 O 符号，表示算法在输入大小 n 趋于无穷大时的渐近行为。

**常见的时间复杂度：**

- O(1)：常数时间，与输入大小无关。
- O(n)：线性时间，与输入大小成正比。
- O(n^2)：平方时间，与输入大小的平方成正比。
- O(log n)：对数时间，与输入大小的对数成正比。

#### 2.2.2 空间复杂度分析

空间复杂度衡量算法执行所需的内存空间。它通常表示为大 O 符号，表示算法在输入大小 n 趋于无穷大时的渐近行为。

**常见的空间复杂度：**

- O(1)：常数空间，与输入大小无关。
- O(n)：线性空间，与输入大小成正比。
- O(n^2)：平方空间，与输入大小的平方成正比。
- O(log n)：对数空间，与输入大小的对数成正比。

**示例：**

考虑以下查找元素的算法：

def find_element(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

此算法的时间复杂度为 O(n)，因为在最坏情况下，它需要遍历整个数组。如果数组很大，则查找元素所需的时间可能会很长。

为了提高效率，我们可以使用二分搜索算法，它利用数组的顺序性质：

def binary_search(arr, target):
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1

    return -1

此算法的时间复杂度为 O(log n)，因为在每次迭代中，它将搜索范围缩小一半。因此，对于大型数组，二分搜索比线性搜索要快得多。

# 3. 算法设计与数据结构

### 3.1 排序算法

排序算法是将一组数据按特定顺序排列的过程。在算法设计中，选择合适的排序算法对于提高算法效率至关重要。

#### 3.1.1 冒泡排序、选择排序和插入排序

**冒泡排序**是一种简单的排序算法，通过反复比较相邻元素，将较大的元素逐个交换到数组末尾。它的时间复杂度为 O(n^2)，其中 n 为数组长度。

def bubble_sort(arr):
    """冒泡排序"""
    for i in range(len(arr) - 1):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

**选择排序**通过逐个找出最小元素并将其与当前位置的元素交换，将数组排序。它的时间复杂度也为 O(n^2)。

def selection_sort(arr):
    """选择排序"""
    for i in range(len(arr) - 1):
        min_idx = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

**插入排序**通过将当前元素与已排序部分逐个比较，将其插入到合适的位置，从而实现排序。它的时间复杂度为 O(n^2)，但对于近乎有序的数组，其效率较高。

def insertion_sort(arr):
    """插入排序"""
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]