树算法：探索树形结构的奥秘，掌握树形算法的精髓

# 1. 树算法基础**

树算法是计算机科学中用于处理树形数据结构的一类算法。树是一种非线性数据结构，它由节点和边组成，其中节点表示数据元素，边表示节点之间的关系。树算法可以用来解决各种问题，例如遍历、搜索、插入和删除树中的元素。

树算法的效率和复杂度取决于树的结构和所使用的算法。对于平衡树（例如二叉搜索树），树算法的时间复杂度通常为 O(log n)，其中 n 是树中的节点数。对于非平衡树，树算法的时间复杂度可能为 O(n)。

# 2. 树形算法理论

### 2.1 树的定义和性质

树是一种重要的非线性数据结构，它由一个根节点和若干个子节点组成。每个子节点可以进一步拥有自己的子节点，形成递归结构。树的性质包括：

- **唯一根节点：**树只有一个根节点，它是树的起点。
- **父子关系：**每个节点只能有一个父节点，但可以有多个子节点。
- **层次结构：**树中的节点按照层次组织，从根节点到叶节点逐层递减。
- **有序性：**树中的子节点通常按照某种顺序排列，例如二叉搜索树中的左子节点小于父节点，右子节点大于父节点。
- **路径唯一性：**从根节点到任何叶节点的路径都是唯一的。

### 2.2 树形算法的基本原理

树形算法是专门针对树形数据结构设计的算法。它们利用树的性质来高效地解决各种问题。树形算法的基本原理包括：

#### 2.2.1 深度优先搜索（DFS）

DFS是一种从根节点开始，沿着一条路径深度遍历树的算法。它递归地访问每个子节点，直到到达叶节点，然后再回溯到父节点继续遍历。DFS适用于查找树中的特定节点或计算树的深度等问题。

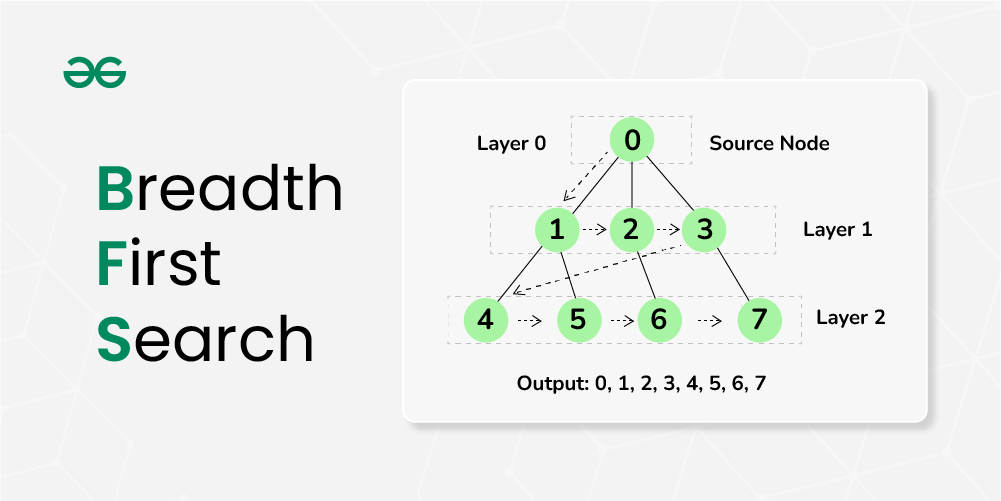
#### 2.2.2 广度优先搜索（BFS）

BFS是一种从根节点开始，逐层遍历树的算法。它将树中的节点放入队列中，然后依次访问队列中的节点，并将其子节点放入队列中。BFS适用于查找树中离根节点最近的节点或计算树的宽度等问题。

### 代码示例：

# 深度优先搜索（DFS）
def dfs(node):
    if node is None:
        return
    # 访问当前节点
    visit(node)
    # 递归访问子节点
    for child in node.children:
        dfs(child)

# 广度优先搜索（BFS）
def bfs(node):
    if node is None:
        return
    queue = [node]
    while queue:
        # 出队并访问当前节点
        current_node = queue.pop(0)
        visit(current_node)
        # 入队子节点
        for child in current_node.children:
            queue.append(child)

# 3.1 树的遍历算法

树的遍历算法是指对树中的所有节点进行访问和处理的过程。常见的树遍历算法包括前序遍历、中序遍历和后序遍历。

#### 3.1.1 前序遍历

**定义：**前序遍历是指先访问根节点，再访问左子树，最后访问右子树。

**代码：**

def preorder_traversal(root):
    """前序遍历二叉树。

    Args:
        root (TreeNode): 根节点。

    Returns:
        list: 遍历结果。
    """
    if not root:
        return []

    result = [root.val]
    result.extend(preorder_traversal(root.left))
    result.extend(preorder_traversal(root.right))

    return result

**逻辑分析：**

* 如果根节点为空，则返回空列表。
* 将根节点的值添加到结果列表中。
* 递归遍历左子树，将结果添加到