【激活函数选择攻略】：打造高效BP神经网络技巧

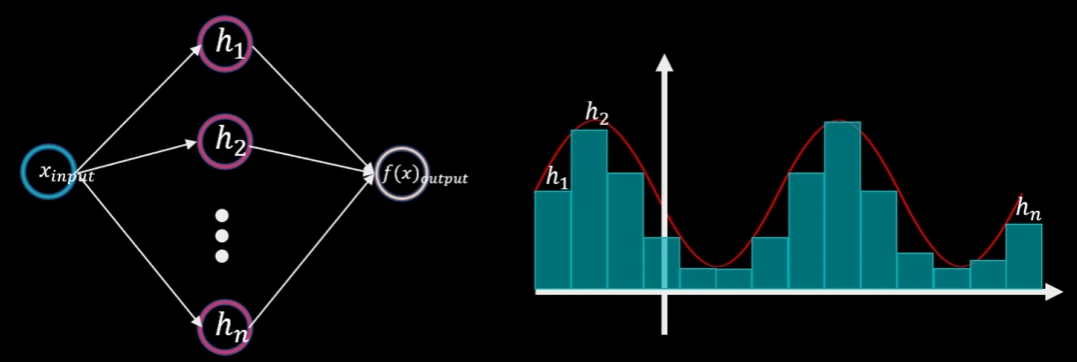
![【激活函数选择攻略】：打造高效BP神经网络技巧](https://img-blog.csdnimg.cn/11b9ddc847814630a681891a6c28095c.png) # 1. 激活函数的作用和重要性激活函数在神经网络中扮演着至关重要的角色，它能够引入非线性因素，帮助神经网络模型更好地学习和逼近复杂的函数关系。通过对输入信号的加权求和后再施加激活函数，可以实现神经网络的非线性映射，从而提高模型的表达能力和灵活性。不同的激活函数具有不同的特点和适用场景，合理选择激活函数不仅可以提升模型性能，还可以避免梯度消失等问题的发生。因此，深入理解和掌握各种激活函数的作用和特性对于构建高效神经网络模型至关重要。 # 2. 常见激活函数及其特点在神经网络中，激活函数是一个非常关键的组成部分，它负责引入非线性特性，提升神经网络的表达能力。在本章中，我们将介绍几种常见的激活函数及它们各自的特点。 ## 2.1 Sigmoid激活函数 ### 2.1.1 定义及数学表达式 Sigmoid激活函数是将输入的实数压缩到(0, 1)之间的函数，其数学表达式为： f(x) = \frac{1}{1 + e^{-x}} ### 2.1.2 特点与应用场景 Sigmoid函数具有平滑的曲线，在二分类问题中常被用作输出层的激活函数，但由于存在梯度消失问题，不适合用于深层神经网络。 ## 2.2 ReLU激活函数 ### 2.2.1 介绍及优势 ReLU激活函数是一种简单而有效的激活函数，其数学表达式为： f(x) = \max(0, x) 相比于Sigmoid和Tanh函数，ReLU函数在梯度更新时更不容易出现梯度消失问题。 ### 2.2.2 Leaky ReLU的改进为了解决ReLU函数在负数部分输出为0的问题，Leaky ReLU引入了一个小的斜率，其数学表达式为： f(x) = \begin{cases} x, & \text{if } x > 0 \\ ax, & \text{otherwise} \end{cases} Leaky ReLU在一定程度上缓解了神经元“死亡”的问题。 ## 2.3 Tanh激活函数 ### 2.3.1 公式和性质 Tanh激活函数是双曲正切函数，将输入值压缩到(-1, 1)之间，其数学表达式为： f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} Tanh函数在输入为0时，输出值接近0，可以将输入归一化到均值为0的状态。 ### 2.3.2 适用范围与局限性 Tanh函数可以用在隐藏层中，但同样存在梯度消失的问题，且输出为0的部分对网络的训练影响较大。 ## 2.4 Softmax激活函数 ### 2.4.1 多分类任务中的应用 Softmax函数通常用于多分类任务，将神经网络的输出转化为各类别的概率分布。其数学表达式为： f(x_{i}) = \frac{e^{x_{i}}}{\sum_{j} e^{x_{j}}} Softmax函数能够有效地处理多分类问题，但在二分类问题中一般不使用。通过对比以上几种常见的激活函数，我们可以发现它们各自的特点及适用场景，合理选择激活函数对于神经网络的训练和性能提升具有重要意义。 # 3. 如何选择适合的激活函数激活函数在神经网络中扮演着至关重要的角色，选择适合的激活函数能够有效提高网络的性能和训练效果。本章将介绍如何根据网络结构和任务需求来选择合适的激活函数，并探讨激活函数的梯度消失问题以及相关解决方法。 ### 3.1 根据网络结构和任务需求选择在实际应用中，选择激活函数需要考虑网络结构的特点和具体任务的需求，下面将从单隐藏层网络和深层神经网络两个方面进行探讨。 #### 3.1.1 单隐藏层网络的最佳选择对于单隐藏层网络，一般常用的激活函数是Sigmoid函数或ReLU函数。Sigmoid函数在输出值范围为(0,1)，适合处理二分类问题，但容易出现梯度消失问题；而ReLU函数能够有效缓解梯度消失问题，对于大规模数据和深度网络训练效果更好。 #### 3.1.2 深层神经网络的适应性在深层神经网络中，由于梯度消失问题的加剧，选择合适的激活函数尤为重要。Leaky ReLU和PReLU等激活函数能够在一定程度上缓解梯度消失问题，提高网络的稳定性和收敛速度。同时，要根据具体任务对激活函数进行选择，确保网络的最终性能。 ### 3.2 激活函数的梯度消失问题梯度消失是指在深层神经网络中，梯度逐渐变小甚至消失，导致网络无法有效学习更新参数，从而影响模型的收敛效果和性能。下面将深入探讨梯度消失对训练的影响以及解决方法。 #### 3.2.1 探讨梯度消失对训练的影响梯度消失会导致网络无法更新权重，导致网络难以收敛，降低模型的拟合能力和泛化能力，影响最终的预测效果。尤其在深度网络中，梯度消失问题更加严重，需要针对性的解决方法。 #### 3.2.2 解决梯度消失的方法为了解决梯度消失问题，可以采取一系列方法，如使用更稳定的激活函数（如ReLU系列）、初始化权重参数（使用Xavier/Glorot初始化）、批量归一化等技术，并结合合适的优化器和学习率调度策略，从而提高网络的训练效果和收敛速度。 ### 3.3 实验验证与对比分析在实际应用中，通过大量实验验证和对比分析不同激活函数的性能表现，可以更好地选择适合任务的激活函数，提高网络的训练效率和预测准确性。在下一章节中，我们将进一步探讨优化BP神经网络的关键技巧，从不同角度提升神经网络的性能和稳定性。至此，我们已经深入探讨了如何选择适合的激活函数，以及梯度消失问题的影响及解决方法。在下一章节中，我们将进一步探讨优化BP神经网络的关键技巧，为神经网络的应用和性能提升提供更多思路和方法。 # 4. 优化BP神经网络的关键技巧 ### 4.1 学习率的设置与调整在训练神经网络时，学习率的设置对模型的性能和收敛速度起着至关重要的作用。过高的学习率容易导致震荡，而过低的学习率则会导致收敛速度过慢。因此，学习率的设置需要谨慎调整。 #### 4.1.1 学习率衰减方法学习率衰减是一种常见的策略，可以在训练过程中逐渐减小学习率，以达到更稳定和高效的优化效果。常见的学习率衰减方法包括指数衰减、时间衰减和余弦退火等。 ```python # 指数衰减示例代码 import tensorflow as tf lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay( initial_learning_rate=0.1, decay_steps=10000, decay_rate=0.9 ) optimizer = tf.keras.optimizers.SGD(learning_rate=lr_schedule) ``` 在上述代码中，我们使用了指数衰减的方法来动态调整学习率，初始学习率为0.1，每10000步衰减一次，衰减率为0.9。 #### 4.1.2 自适应学习率算法自适应学习率算法是根据模型的表现实时调整学习率的一种方法，常见的自适应学习率算法有 Adagrad、RMSprop 和 Adam 等。 ```python # Adam优化器示例代码 optimizer = tf.keras.optimizers.Adam(learning_rate=0.001) ``` Adam 是一种结合了动量梯度下降和RMSprop的优化算法，通过计算梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率。 ### 4.2 权重初始化策略神经网络的初始化对模型的训练和性能同样具有重要影响，良好的权重初始化可以加速收敛并提高模型的泛化能力。 #### 4.2.1 随机初始化的必要性在深度神经网络中，如果将所有的权重初始化为相同的值，会导致网络对称性问题，使得网络无法学习更复杂的特征。因此，采用随机初始化可以打破对称性，更好地训练网络。 #### 4.2.2 常用的权重初始化方法常用的权重初始化方法包括随机初始化、Xavier 初始化和 He 初始化等。 ```python # Xavier初始化示例代码 initializer = tf.initializers.GlorotUniform() model.add(Dense(64, activation='relu', kernel_initializer=initializer)) ``` Xavier 初始化是一种根据输入和输出神经元数量自适应调整权重初始化范围的方法，有助于避免梯度消失和梯度爆炸问题。 ### 4.3 批量归一化技术批量归一化是一种通过规范化输入数据分布来加速深度网络训练的技术，能够有效缓解梯度消失和梯度爆炸问题，加快模型的收敛速度。 #### 4.3.1 介绍与原理批量归一化在每个训练小批量上进行归一化，通过减少内部协变量偏移（Covariate Shift）来加速网络的训练。其原理是对每个特征进行归一化处理，使得其分布稳定。 ```python # 批量归一化示例代码 model = Sequential() model.add(Dense(64, input_shape=(10,))) model.add(BatchNormalization()) model.add(Activation('relu')) ``` #### 4.3.2 批量归一化对梯度传播的影响批量归一化不仅可以加速收敛，还可以降低对初始化的依赖性，提高模型的稳定性。它通过将每一层的输入归一化到均值为0，方差为1的分布中，使得网络更容易训练。通过合理设置学习率、权重初始化策略和批量归一化技术，可以有效优化 BP 神经网络，提高模型的训练效率和性能。以上是优化BP神经网络的关键技巧，包括学习率的设置与调整、权重初始化策略以及批量归一化技术。这些技巧在实际神经网络训练中起着至关重要的作用，能够帮助提升模型的性能和收敛速度。 # 5. 案例分析与实战应用探讨 ### 5.1 BP神经网络在图像分类任务中的应用在实际的图像分类任务中，BP神经网络经常被应用于特征提取和模式识别。接下来我们将深入探讨BP神经网络在图像分类中的具体应用，并分析激活函数选择对性能的影响。 #### 5.1.1 数据预处理与特征提取首先是数据预处理，这一步非常重要，通常包括图像的读取、缩放、标准化等操作。对图像进行预处理可以提高模型训练的效率和收敛速度，同时能够降低模型过拟合的风险。接着是特征提取，通过卷积神经网络（CNN）等方法可以有效提取图像的特征。特征提取的好坏直接影响着模型对图像的理解和分类准确率。在BP神经网络中，激活函数的选择对特征提取至关重要。 #### 5.1.2 激活函数选择对性能的影响不同的激活函数在图像分类任务中会产生不同的效果。例如，ReLU函数在深层网络中能够有效缓解梯度消失问题，适用于加速模型的收敛速度。而Sigmoid函数则可以将输出的结果映射到0到1之间，常用于多分类任务中。另外，Leaky ReLU函数通过引入一定的负数斜率，使得神经元在负数区域也能有激活状态，从而避免了ReLU函数的神经元“死亡”现象。在图像分类中，合理选择激活函数能够提升模型的分类精度和泛化能力。 ### 5.2 BP神经网络在文本情感分析中的实际应用文本情感分析是自然语言处理领域中一项重要的任务，通过对文本内容进行分析，自动识别其表达的情感倾向。下面我们将介绍BP神经网络在文本情感分析中的实际应用情况，并具体讨论构建模型过程中的激活函数选择。 #### 5.2.1 构建模型并选择激活函数在文本情感分析任务中，通常需要将文本数据转化为数值型数据进行处理。可以利用词嵌入（Word Embedding）等技术将文本转换为密集向量表示，作为神经网络的输入。在构建BP神经网络模型时，选择合适的激活函数对于提高情感分类的准确性非常关键。常用的激活函数如ReLU、Tanh等也可以被应用于文本情感分析中，不同的激活函数可能对模型的学习效果产生显著影响。因此，在构建文本情感分析模型时，需要针对具体任务选择最适合的激活函数。 #### 5.2.2 训练过程与效果评估训练BP神经网络模型时，通常采用随机梯度下降（SGD）等优化算法不断更新模型参数，使得模型逐渐收敛到最优解。在训练过程中需要监控模型的损失函数变化，以及在验证集上的表现情况，及时调整模型结构和超参数。通过对文本情感分析任务中不同激活函数的比较实验，并评估模型在测试集上的性能，可以更好地理解激活函数对模型精度和泛化能力的影响，进而优化模型的设计和训练过程。