【梯度检验方法分析】： BP神经网络优化关键技巧

# 1. 梯度下降算法简介

梯度下降算法是机器学习领域中一种常用的优化方法，通过不断迭代更新参数，使得损失函数值不断减小，达到模型最优解的目的。其核心思想是沿着梯度的反方向更新参数，以减少损失函数的值。梯度下降算法包括批量梯度下降、随机梯度下降和小批量梯度下降等不同的变种，适用于各种机器学习模型的训练过程中。

通过梯度下降算法，可以不断调整模型参数，提高模型的拟合能力和泛化能力，是深度学习领域中不可或缺的重要优化技巧之一。

# 2.1 神经网络基本原理

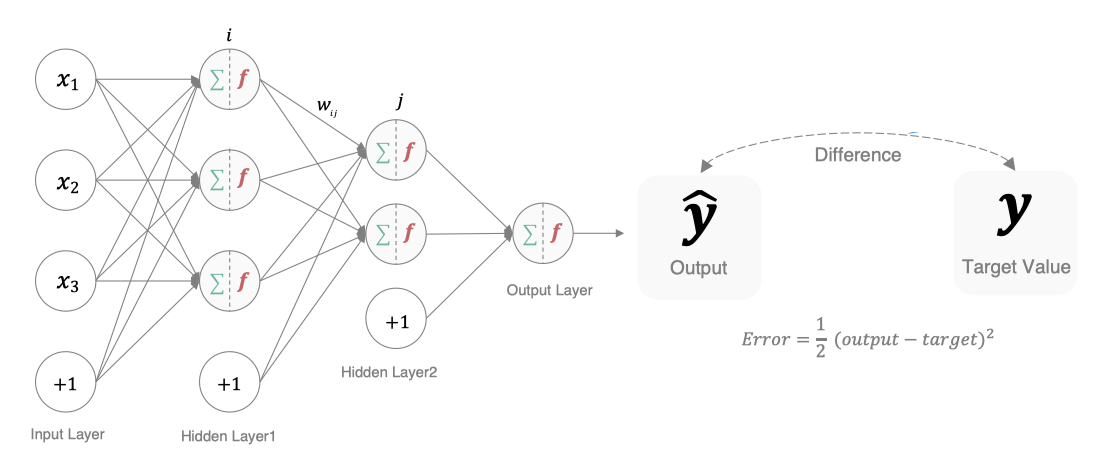
神经网络作为一种模仿人脑神经元网络构建的机器学习算法，在深度学习领域中发挥着关键作用。本节将介绍神经网络的基本原理，包括感知器模型、激活函数和前向传播。

### 2.1.1 感知器模型

感知器是一种人工神经元模型，由美国心理学家Frank Rosenblatt在1957年提出。它是神经网络中最基本的结构单元，接收输入信号，对输入进行加权处理，并通过激活函数输出结果。感知器模型的数学表示可以描述为：
$$y = f(\sum_{i=1}^{n} w_i x_i + b)$$
其中，$x_i$为输入，$w_i$为权重，$b$为偏置项，$f$为激活函数。

### 2.1.2 激活函数

激活函数在神经网络中扮演着非常重要的角色，它引入了非线性因素，使得神经网络具备了强大的表达能力。常见的激活函数包括Sigmoid、ReLU、Tanh等。激活函数的选择会直接影响神经网络的性能和训练效果。

### 2.1.3 前向传播

前向传播是神经网络中的一种信息传递方式，即输入数据从输入层经过一层层的神经元传递，最终得到输出结果。在前向传播过程中，每个神经元都将上一层的输出乘以对应的权重，经过激活函数后传递给下一层。

## 实现前向传播
以下是一个简单的前向传播函数示例，计算单个神经元的输出结果：

# 定义激活函数ReLU
def ReLU(x):
    return max(0, x)

# 定义一个神经元的前向传播函数
def forward_propagation(inputs, weights, bias):
    total = sum([x * w for x, w in zip(inputs, weights)]) + bias
    return ReLU(total)

# 测试前向传播
inputs = [1, 2, 3]
weights = [0.1, 0.2, 0.3]
bias = 0.5
output = forward_propagation(inputs, weights, bias)
print(f'神经元的输出结果为: {output}')

通过上述代码，可以实现单个神经元的前向传播过程，计算得到输出结果。

以上是神经网络基本原理的介绍，包括感知器模型、激活函数和前向传播。神经网络的搭建是基于这些基本原理进行的，理解这些原理有助于我们深入学习神经网络的更高级应用。

# 3. 梯度检验方法详解

梯度检验是神经网络优化中的关键步骤，通过对神经网络的梯度进行检验，可以验证反向传播算法的正确性，避免梯度消失或梯度爆炸等问题。本章将深入探讨为什么需要梯度检验、梯度检验的原理，以及如何在实践中应用梯度检验方法。

### 3.1 为什么需要梯度检验

梯度在神经网络优化中的重要性不言而喻，它代表了损失函数关于权重的变化率。然而，由于复杂的神经网络结构和激活函数的非线性性，梯度的计算往往容易出现错误。梯度消失和梯度爆炸是常见的问题，会导致模型无法有效训练，因此需要引入梯度检验方法来验证梯度的准确性。

#### 3.1.1 梯度在神经网络优化中的重要性

在神经网络的训练过程中，梯度是参数更新的依据，通过沿着梯度的方向不断调整参数，使得模型逐渐收敛到最优解。梯度的正确计算对于模型的收敛速度和性能影响巨大。

#### 3.1.2 梯度消失和梯度爆炸问题

梯度消失是指在反向传播过程中，梯度逐渐变小，导致参数无法得到