【Python排序进阶】：递归在排序中的应用与理解

# 1. 排序算法概述与递归基础

排序算法是计算机科学中用于将元素集合按照一定的顺序进行排列的过程。这一章旨在为您提供排序算法的基础知识以及递归技术的介绍，为后续章节中递归排序算法的深入探讨打下坚实的基础。

## 1.1 排序算法的重要性

排序算法在数据处理和分析中扮演着至关重要的角色。良好的排序不仅可以加快查找速度，还能提升数据处理效率。对数据进行排序，常用于数据库查询、搜索引擎、数据分析及可视化等场景。

## 1.2 递归思想简介

递归是一种编程技巧，它允许函数调用自身来解决问题。在排序算法中，递归能够将大问题分解为小问题，逐一解决，直至找到最终解决方案。递归的关键在于找到递归的基准情况和递归的规则。

## 1.3 递归与迭代的对比

递归和迭代是解决同一问题的两种不同方法。递归在某些情况下使代码更简洁易懂，但可能引起栈溢出或性能下降。迭代通常需要更多的状态管理和循环控制，但往往更高效。正确选择使用哪种方法取决于特定问题的需求。

# 2. 递归思想在排序算法中的应用

## 2.1 递归的基本概念

### 2.1.1 递归的定义与工作原理

递归是一种在程序设计中广泛使用的编程技术，它允许函数直接或间接地调用自身。递归函数的工作原理是通过反复调用自身来逐步缩小问题的规模，直到达到一个简单到可以直接解决的基本情况（base case），然后逐层返回解决问题。

递归工作原理的核心可以概括为三个步骤：

1. **基准情形（Base Case）**：这是递归的终点，为递归提供了一个停止的条件。如果没有基准情形，递归将会无限进行下去，导致栈溢出或程序崩溃。
2. **递归情形（Recursive Case）**：在递归的每一步，我们都会将问题分解为更小的子问题，并调用函数自身来解决这些子问题。
3. **解决步骤（Progress toward Base Case）**：确保每次递归调用都会使问题的规模更接近基准情形，否则递归将永无止境。

### 2.1.2 递归与迭代的对比

递归和迭代是实现重复计算的两种主要方法，它们各有优劣。

**递归的优缺点：**

- 优点：
- **代码简洁易懂**：递归代码往往更符合直觉，且易于实现复杂算法。
- **逻辑清晰**：问题分解的层次结构使得逻辑更加清晰。
- 缺点：
- **效率问题**：每次递归调用都会增加函数的调用栈，可能造成栈溢出，且递归过程中的重复计算也会影响性能。
- **空间开销**：相对于迭代，递归通常需要更多的内存空间。

**迭代的优缺点：**

- 优点：
- **性能较好**：迭代避免了递归调用的额外开销，通常比递归执行得更快。
- **空间效率高**：迭代不需要额外的函数调用栈空间。
- 缺点：
- **编写复杂**：对于某些算法，迭代版本可能需要更复杂的循环和状态管理。

## 2.2 递归在排序算法中的角色

### 2.2.1 递归排序算法的优势

递归排序算法如快速排序、归并排序等在处理大量数据时，能够展现出优雅的结构和较高的效率。其优势主要体现在：

- **清晰的逻辑结构**：递归算法通常能提供直观且逻辑性强的解决方案，尤其适用于需要递归地分割问题的场景。
- **高效的分解策略**：对于分而治之的算法，递归提供了一种自然的处理数据的方式，使得问题能够被有效地分解和组合。
- **优化的潜力**：递归算法往往能够通过某些优化技术，例如尾递归优化，达到与迭代相当甚至更好的性能。

### 2.2.2 递归排序算法的挑战与解决策略

尽管递归排序算法在某些方面具有优势，它们也面临一些挑战：

- **内存开销**：递归调用增加栈空间的需求，可能导致栈溢出。解决这一问题的方法之一是使用尾递归优化。
- **性能问题**：递归可能导致重复计算，影响算法的效率。为了解决这个问题，可以通过存储已经计算过的结果（记忆化）来避免重复计算。

**解决策略示例：**

尾递归优化是一种特殊的递归形式，它的特点是函数的最后一次递归调用是整个函数体的最后一个动作。这样可以使得编译器能够进行优化，使得每次递归调用都是在同一个栈帧上完成，减少调用栈的增长。

def tail_recursive_factorial(n, accumulator=1):
    if n == 0:
        return accumulator
    return tail_recursive_factorial(n - 1, accumulator * n)

## 2.3 常见的递归排序算法

### 2.3.1 快速排序算法的递归实现

快速排序是一种典型的分治算法，其基本思想是：选择一个元素作为基准（pivot），通过一趟排序将待排记录分隔成独立的两部分，其中一部分的所有记录均比另一部分的所有记录小，然后再分别对这两部分记录继续进行排序，以达到整个序列有序。

快速排序的递归实现中，递归主要体现在将大问题分解为小问题的策略上：

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

### 2.3.2 归并排序算法的递归实现

归并排序同样是一种分治算法，它的思想是将原始数组分成较小的数组，直到每个小数组只有一个位置，然后将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

在归并排序中，递归体现在将数组拆分成两个子数组的过程，然后递归地对这两个子数组进行排序，最后将排序好的子数组归并起来：

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

def merge(left, right):
    sorted_arr = []
    while left and right:
        if left[0] <= right[0]:
            sorted_arr.append(left.pop(0))
        else:
            sorted_arr.append(right.pop(0))
    sorted_arr.extend(left or right)
    return sorted_arr

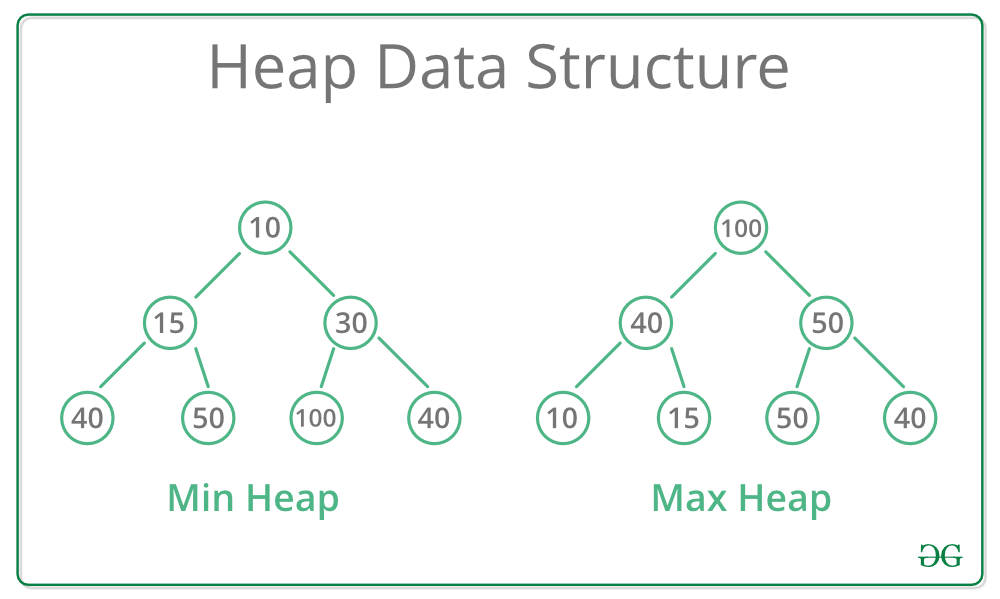
### 2.3.3 堆排序算法与递归的结合

堆排序是一种使用二叉堆数据结构的比较排序算法。在堆排序过程中，递归主要用于构建和维持堆的性质，即堆的每个父节点的值都大于或等于其子节点的值。

堆排序涉及递归的地方主要是在调整堆的操作中。构建初始堆和将数组中的每个元素一个个取出并维持堆性质，都是通过递归函数实现的。

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # Build a maxheap.