【Python内存优化】：分析与优化排序算法的内存消耗

# 1. Python内存优化概述

在今天的编程实践中，Python因其易用性和强大的库支持而广受欢迎。但是，由于其高级特性，Python在性能和内存管理方面存在某些局限性。随着数据量的增长，不恰当的内存使用会严重影响程序性能，导致效率低下。优化Python代码的内存使用，尤其是在数据处理和排序操作中，已成为提升性能的关键因素。本文将深入探讨Python内存优化的重要性、原理以及实施策略，帮助IT专业人士掌握高效内存管理的技巧，从而提高应用程序的响应速度和处理能力。

# 2. Python中排序算法的内存分析

## 2.1 排序算法的内存占用原理

### 2.1.1 理解Python内存管理

Python 的内存管理是一个复杂且强大的系统，它自动分配和释放内存，这大大简化了程序的开发。然而，对内存管理机制的理解是进行内存优化的前提。Python 使用一个名为引用计数（reference counting）的机制来跟踪内存的使用。每个对象都有一对与之关联的引用计数和值，当引用计数降到零时，内存会被自动回收。此外，Python 还使用了一个周期性运行的垃圾回收器来处理循环引用的问题。虽然 Python 的自动内存管理减轻了开发者的负担，但在大数据集上进行操作时，如果不注意内存使用效率，可能会导致程序效率低下甚至崩溃。

### 2.1.2 排序算法的内存占用特点

排序算法在进行元素的比较和交换过程中，会产生临时变量，这些临时变量会占用额外的内存空间。例如，在冒泡排序中，每进行一次元素比较，就可能产生一个临时变量。在快速排序中，递归调用栈的深度决定了额外内存的使用量。不同排序算法的内存占用差异较大，了解这些差异有助于我们针对不同的应用场景选择合适的排序算法，从而优化内存使用。

## 2.2 常用排序算法的内存消耗对比

### 2.2.1 冒泡排序、选择排序与插入排序

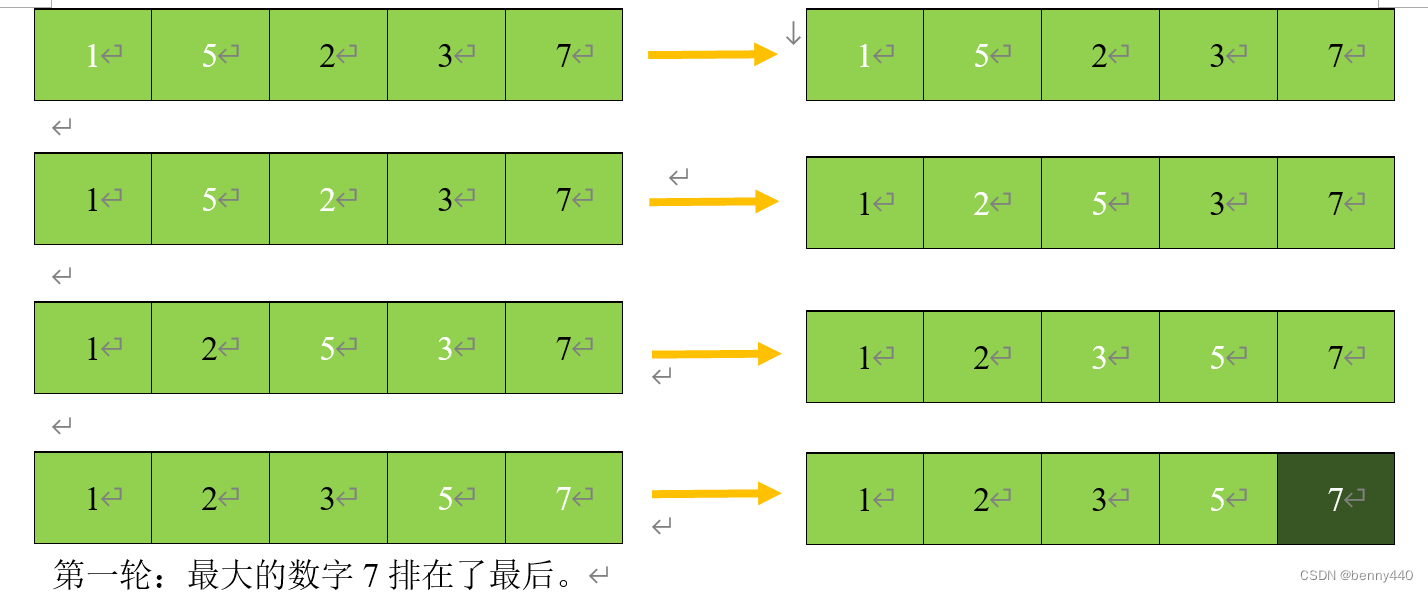
#### 冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法，它通过重复遍历待排序的列表，比较相邻元素并交换它们的位置，如果它们不在正确的位置上。它的时间复杂度为O(n^2)，空间复杂度为O(1)，因为除了输入的列表外，它不需要额外的存储空间。然而，冒泡排序过程中会产生许多不必要的元素交换，这些交换操作会带来额外的内存开销。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

在冒泡排序中，虽然不需要额外空间，但通过 `arr[j], arr[j+1] = arr[j+1], arr[j]` 的交换操作，涉及到了三次变量赋值操作，对于大规模数据集来说，这样的交换会占用较多的临时内存。

#### 选择排序（Selection Sort）

选择排序算法的时间复杂度也是O(n^2)，但它在每次迭代中只使用常数空间，即O(1)的空间复杂度。它通过选择未排序部分的最小（或最大）元素，然后将其放到已排序序列的末尾来工作。虽然其内存效率高，但由于需要反复遍历未排序部分，因此其总体性能并不理想。

def selection_sort(arr):
    for i in range(len(arr)):
        min_idx = i
        for j in range(i+1, len(arr)):
            if arr[min_idx] > arr[j]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

在这段代码中，变量 `min_idx` 用于记录最小元素的索引，没有其他额外的内存需求。但是，每次比较都需要记录下当前找到的最小值索引，会增加一些不必要的计算和内存使用。

### 2.2.2 快速排序与归并排序

#### 快速排序（Quick Sort）

快速排序通常采用分治策略，其平均时间复杂度为O(n log n)，空间复杂度为O(log n)。尽管快速排序在内存效率上比其他算法（如归并排序）有优势，但其最差情况下的时间复杂度为O(n^2)，且需要递归调用栈，这意味着在栈空间上的消耗随着数据规模的增大而增大。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

递归调用过程中，每个递归实例都需要保存其局部变量。在上面的代码中，每次递归调用的参数 `arr`、中间变量 `left`、`middle` 和 `right` 都需要在调用栈上分配空间。

#### 归并排序（Merge Sort）

归并排序是另一个时间复杂度为O(n log n)的排序算法，但它的空间复杂度为O(n)，因为每次合并操作都需要与原数组一样大小的额外空间。虽然归并排序在处理大型数据集时表现优秀，但由于需要额外的存储空间，因此在内存敏感的应用场景下可能不是最佳选择。

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

def merge(left, right):
    result = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j