【Python排序深度解析】：掌握堆排序与归并排序的精髓

# 1. Python排序算法概述

## 1.1 排序算法的重要性

在计算机科学中，排序算法是基本且重要的算法之一，它们的性能影响着数据处理的效率。Python，作为一种高级编程语言，内置了多种排序机制，同时也支持开发者实现自己的排序逻辑。排序算法的效率取决于数据规模、数据类型和特定应用场景。在后续章节，我们将深入探讨Python中常见的堆排序和归并排序算法。

## 1.2 常见的排序算法

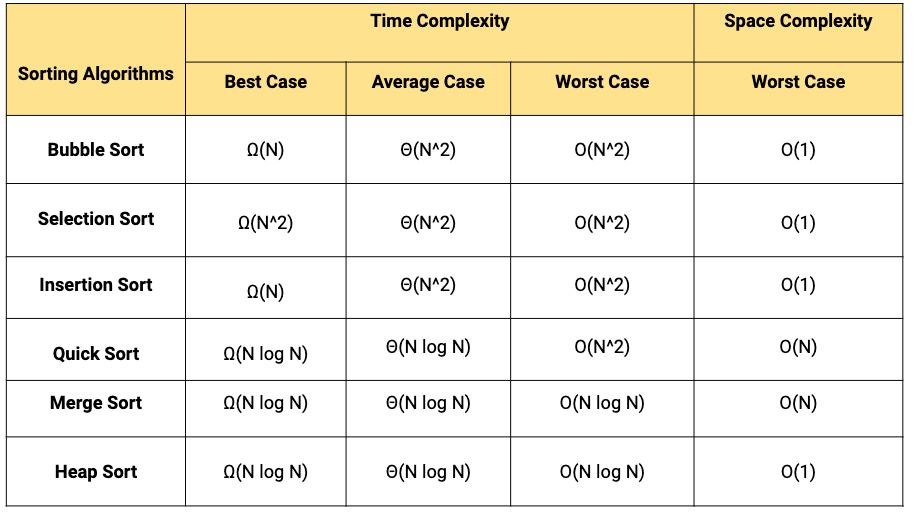
排序算法多种多样，常见的包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等。在Python中，内置的排序算法经过高度优化，但了解和掌握不同排序算法的原理对于编写高效的代码是很有必要的。

## 1.3 选择排序算法的标准

选择合适的排序算法通常基于以下标准：算法的时间复杂度、空间复杂度、是否稳定、是否需要额外的存储空间以及是否适合特定类型的数据。对于Python开发者来说，理解这些算法的工作原理可以帮助他们针对不同的问题场景做出最佳选择。

# 2. 堆排序的理论与实现

堆排序是计算机科学中一种经典的比较排序算法。它利用堆这种数据结构的特性来进行排序。接下来，我们将深入探讨堆排序的基本概念、实现方法以及时间复杂度和空间复杂度分析。

## 2.1 堆排序的基本概念

堆是一种特殊的完全二叉树，其中每个父节点的值都大于或等于其子节点的值（对于最大堆），或者每个父节点的值都小于或等于其子节点的值（对于最小堆）。堆排序的核心思想是利用堆这种数据结构进行排序。

### 2.1.1 堆结构的定义和性质

堆可以被看作是一棵用数组来表示的完全二叉树。其性质如下：

- **堆性质**：对于每个非叶子节点i，其值必须大于或等于其子节点的值（最大堆），或者小于或等于其子节点的值（最小堆）。
- **完全二叉树**：除了最后一层外，每一层都被完全填满，并且最后一层的节点都集中在左边。
- **索引关系**：对于任意一个非根节点i，其父节点索引为(i-1)/2（向下取整），其左子节点索引为2i+1，右子节点索引为2i+2。

堆排序的优势在于其近似的对数时间复杂度，这使得它在处理大量数据时非常有效。

### 2.1.2 堆排序的原理和步骤

堆排序分为两个主要步骤：

1. **构建堆**：首先将输入的数据构建成一个最大堆或最小堆。
2. **排序过程**：将堆顶元素与堆的最后一个元素交换，然后对剩余的n-1个元素重新调整为最大堆或最小堆。重复这个过程，直到堆的大小为1，排序完成。

堆排序的关键在于调整堆的过程，确保每次移除最大元素（或最小元素）后，剩余的元素仍然满足堆的性质。

## 2.2 堆排序的Python实现

### 2.2.1 Python中的堆操作函数

Python标准库中`heapq`模块提供了对堆的支持。以下是`heapq`模块中与堆相关的函数：

- `heapq.heappush(heap, item)`：将item压入堆中，保持堆的性质。
- `heapq.heappop(heap)`：弹出堆中的最小项，并保持堆的性质。
- `heapq.heapify(heap)`：将list转换为堆，过程需要O(n)时间复杂度。

这些函数为我们提供了构建堆和调整堆所必需的操作。

### 2.2.2 构建最大堆与最小堆

在Python中，我们可以直接使用`heapq`模块来实现最大堆和最小堆的构建。以下是构建最大堆和最小堆的示例代码：

import heapq

def build_max_heap(arr):
    return heapq.heapify(arr)

def build_min_heap(arr):
    return heapq.heapify(arr)

# 示例数组
arr = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
max_heap = build_max_heap(arr.copy())
min_heap = build_min_heap(arr.copy())

print("Max Heap:", list(max_heap))
print("Min Heap:", list(min_heap))

### 2.2.3 堆排序算法的完整代码

有了前面的基础，我们可以实现堆排序算法，它包括构建堆、不断调整堆和弹出堆顶元素的过程：

import heapq

def heap_sort(arr):
    # 构建最大堆
    heapq.heapify(arr)
    sorted_arr = []
    # 不断弹出最大元素
    while arr:
        sorted_arr.append(heapq.heappop(arr))
    return sorted_arr

# 示例数组
arr = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
sorted_arr = heap_sort(arr)
print("Sorted Array:", sorted_arr)

### 2.3 堆排序的复杂度分析

#### 2.3.1 时间复杂度分析

堆排序的时间复杂度主要由两个阶段决定：

- **构建堆**：在最佳情况下，需要O(n)时间复杂度。在最差情况下，需要O(n log n)时间复杂度。
- **排序过程**：由于每次从堆中移除元素需要O(log n)时间，且总共进行n-1次移除，因此排序过程的时间复杂度为O(n log n)。

综合以上两个阶段，堆排序的总时间复杂度为O(n log n)。

#### 2.3.2 空间复杂度分析

堆排序的空间复杂度为O(1)，因为它只需要常数级别的额外空间，除了输入数组外，不需要其他额外空间来存储数据结构。在Python实现中，`heapq`模块的函数直接在输入数组上进行操作。

以上内容涵盖了堆排序的理论基础、Python实现和复杂度分析，希望能够帮助读者深入理解堆排序的内部机制，并在实际编程中加以应用。接下来的章节将继续介绍归并排序，以及堆排序与归并排序的性能比较，以及排序算法在实际中的应用和高级拓展。

# 3. 归并排序的理论与实现

## 3.1 归并排序的基本概念

### 3.1.1 归并排序的分治策略

归并排序是一种应用分治策略的排序算法。它将一个大列表分割成两个子列表，直到每个子列表只包含一个元素。接着，它将这些子列表重新组合起来，使得合并后的列表是有序的。这个过程很像逐步将一本书撕成单页，然后再按正确的顺序将这些页码粘合起来。

分治策略可以分为三个步骤：分解、解决和合并。
- 分解：将列表分割成n个子列表，每个子列表包含一个元素（认为一个元素是有序的）。
- 解决：递归地应用归并排序来排序这些子列表。
- 合并：将已排序的子列表合并成最终的排序列表。

分治策略的关键在于合并过程，这要求算法能够高效地合并两个有序列表。

### 3.1.2 归并排序的递归过程

归并排序的递归过程是算法的核心。在递归的每一步，我们都要解决两个子问题，并将这两个已经排序好的子列表合并。递归调用的终止条件是子列表的长度为1，此时列表已经是有序的。

递归过程可以描述如下：
- 递归地将列表分成更小的部分直到列表长度为1。
- 合并这些单元素列表以形成有序的列表。
- 继续合并更长的有序列表，直到合并成原始列表的长度。

这个过程在视觉上可以理解为合并“溪流”以形成“河流”，最终构建出“海洋”。

## 3.2 归并排序的Python实现

### 3.2.1 分割列表函数的实现

要实现归并排序，首先需要一个分割列表的函数。该函数会递归地将列表分为更小的部分，直至到达只有一个元素的列表。

以下是分割函数的实现：