学习率+动量：深度学习中的高效组合策略

# 1. 深度学习优化问题概述

深度学习模型的性能在很大程度上取决于其优化过程的效率和效果。优化问题主要关注如何调整模型参数以最小化损失函数。本章将简要介绍深度学习优化问题的相关概念，为后文学习率和动量法等高级优化技术的深入讨论奠定基础。

在训练过程中，模型会根据损失函数计算出的梯度进行参数更新。理想情况下，我们希望损失函数能够迅速且稳定地向最小值下降。然而，由于数据集的复杂性、非凸性以及梯度的稀疏性等因素，这一过程往往充满了挑战。

为了解决这些问题，研究者们提出了多种优化算法和技术。这些方法不仅包括调整学习率的策略，也包括动量法、正则化以及自适应调整参数的高级优化算法。通过这些技术的应用，深度学习模型能够在实际的机器学习任务中实现更优的表现和更高的训练效率。接下来的章节中，我们将对这些优化策略进行详细探讨。

# 2. 学习率的基本理论与应用

### 2.1 学习率的定义与作用

#### 2.1.1 损失函数与梯度下降

在优化问题中，损失函数（或目标函数）衡量模型预测值与真实值之间的差异。梯度下降是一种基本的优化算法，它的核心思想是利用损失函数的梯度信息来更新模型参数，从而达到减少损失的目的。具体来说，参数在损失函数梯度的负方向上移动一定的步长（即学习率）来更新参数值。

以线性回归为例，模型的目标函数通常是均方误差，模型参数包括权重和偏置。利用梯度下降法，可以得到如下更新规则：

theta_new = theta_old - learning_rate * gradient

这里，`theta_new` 和 `theta_old` 分别代表参数更新前后值，`learning_rate` 是学习率，`gradient` 是目标函数关于参数的梯度。

#### 2.1.2 学习率对优化过程的影响

学习率是一个超参数，它决定了在参数空间中每一步的步长大小。学习率过大可能会导致收敛困难，甚至在最优解附近震荡或发散；而学习率过小则可能导致优化过程非常缓慢，甚至陷入局部最小值。因此，选择合适的学习率是优化问题中的一个关键步骤。

### 2.2 学习率的调整策略

#### 2.2.1 固定学习率策略

固定学习率是最简单的调整策略，它在整个训练过程中保持学习率不变。虽然这种策略易于实现，但其缺点是无法适应数据的复杂性和优化过程中的不同阶段。

for epoch in range(num_epochs):
    for batch in data_loader:
        update_parameters(batch, fixed_learning_rate)

在上述伪代码中，`fixed_learning_rate` 是预先设定的一个固定值，`update_parameters` 表示更新网络参数的函数。

#### 2.2.2 自适应学习率策略

自适应学习率策略会根据训练过程中的信息动态调整学习率。这通常涉及到对历史梯度信息的分析，比如 RMSprop 和 Adam 这两种流行的优化算法。

for epoch in range(num_epochs):
    for batch in data_loader:
        update_parameters(batch, adaptive_learning_rate)

在这里，`adaptive_learning_rate` 根据某种规则（如RMSprop中的梯度平方和的移动平均）进行更新。

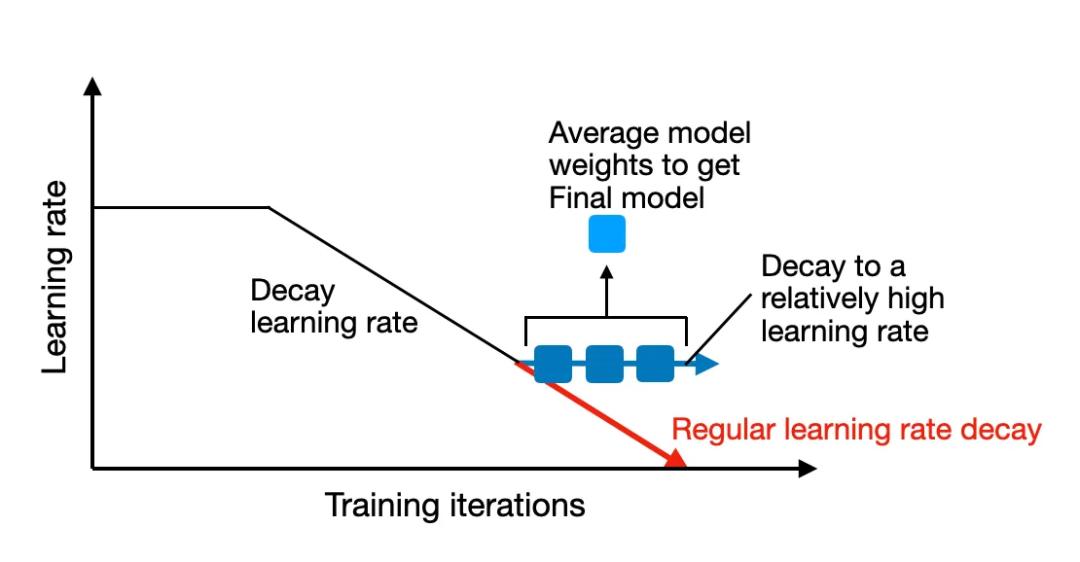
#### 2.2.3 学习率衰减技术

学习率衰减是一种逐渐减少学习率的方法。随着训练的进行，学习率逐步减小，有助于模型在最终阶段进行更精细的调整。

initial_learning_rate = 0.1
decay_rate = 0.1
for epoch in range(num_epochs):
    current_learning_rate = initial_learning_rate * decay_rate ** epoch
    for batch in data_loader:
        update_parameters(batch, current_learning_rate)

在上述代码中，学习率按照指数衰减的方式随着 `epoch` 增加而逐渐减小。

### 2.3 学习率的选择与调优

#### 2.3.1 超参数搜索方法

学习率的搜索可以通过网格搜索、随机搜索或贝叶斯优化等方法进行。在实践中，通常使用验证集来评估不同学习率下的模型性能，从而选择最佳的学习率。

#### 2.3.2 学习率调度器的实现与应用

学习率调度器能够根据训练进度动态调整学习率。大多数深度学习框架已经内置了学习率调度器，如 PyTorch 的 `StepLR` 和 `ReduceLROnPlateau`。

optimizer = torch.optim.SGD(model.parameters(), lr=initial_learning_rate)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(num_epochs):
    train_one_epoch()
    scheduler.step()

在上面的代码中，学习率在每 `step_size` 个 epoch 后会乘以 `gamma`。

表格、mermaid流程图和代码块的展示：

| 学习率策略 | 适用场景 | 优点 | 缺点 |
| --- | --- | --- | --- |
| 固定学习率 | 简单快速 | 易于实现 | 适应性差 |
| 自适应学习率 | 需要动态调整学习率 | 能适应复杂数据和训练阶段 | 实现相对复杂 |
| 学习率衰减 | 需要模型逐渐收敛 | 可避免过早收敛到局部最小值 | 需要合适的衰减策略 |

graph TD
A[开始训练] --> B[固定学习率策略]
A --> C[自适应学习率策略]
A --> D[学习率衰减技术]
B --> E[收敛速度取决于学习率]
C --> F[动态调整学习率]
D --> G[逐步减小学习率]

# 示例：自适应学习率策略
# 这里是使用Adam优化器的伪代码

optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
for epoch in range(num_epochs):
    for batch in data_loader:
        loss = compute_loss(batch)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

以上章节内容详细阐述了学习率在深度学习中的基本理论和应用，包括学习率的定义、作用、调整策略以及如何