学习率与神经网络训练：影响研究与优化策略

# 1. 学习率在神经网络训练中的作用

神经网络训练是一个复杂的优化过程，而学习率（Learning Rate）是这个过程中的关键超参数之一。学习率决定了在优化过程中，模型参数更新的步长大小。如果学习率设置得过高，可能会导致模型无法收敛，而过低的学习率则会使训练过程过慢，且有可能陷入局部最小值。选择合适的学习率，对提高模型性能、加速训练过程以及避免梯度消失或爆炸等问题至关重要。

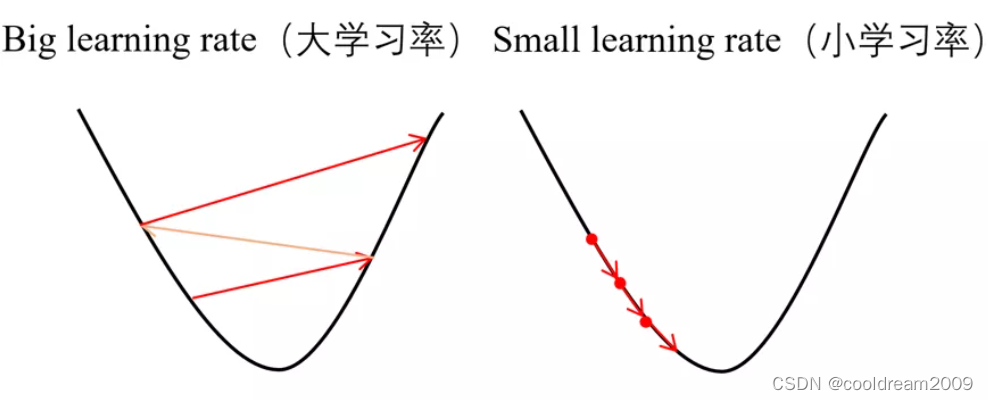
学习率的调整能够影响模型的学习效率和最终性能。例如，在训练初期，较大的学习率可以帮助模型快速朝着正确的方向前进；而在后期，较小的学习率则有助于模型进行精细化调整，以达到更好的收敛效果。正确管理学习率，往往是训练高性能神经网络模型的关键所在。

# 2. 学习率的基础理论与类型

## 2.1 学习率的定义与重要性

### 2.1.1 传统机器学习中的学习率

在传统机器学习算法中，学习率是控制模型在优化过程中权重更新幅度的超参数。它决定了算法在参数空间移动的步长大小。如果学习率过大，可能会导致算法无法收敛到最优解，而是在最优解附近震荡，甚至发散；如果学习率太小，则会导致收敛速度过慢，需要更多的时间来完成训练，有时甚至会卡在局部最小值。

举个例子，在梯度下降算法中，学习率影响着每一个参数更新的量：

# 示例代码：梯度下降法中学习率的应用
for each_epoch in range(number_of_epochs):
    for each_sample in training_dataset:
        gradients = compute_gradient(each_sample)
        weights -= learning_rate * gradients

在此代码段中，`learning_rate` 直接决定了参数 `weights` 更新的幅度。`compute_gradient` 函数负责计算当前样本的梯度。

### 2.1.2 深度学习中学习率的特殊性

在深度学习中，学习率的角色变得更加复杂和重要。深度神经网络的参数数量远超传统机器学习模型，其优化过程对学习率极其敏感。由于网络的深度和宽度，如果学习率选择不当，网络训练可能会出现梯度爆炸或梯度消失的问题。

深度学习模型通常会采用各种技术来维持或恢复学习率的重要性，例如使用学习率预热（warm-up）或者学习率衰减（decay）来适应复杂的数据分布，使得模型能够稳定地学习。

## 2.2 学习率的类型与选择

### 2.2.1 固定学习率与动态学习率

在早期的神经网络训练过程中，很多研究者和工程师倾向于使用固定的全局学习率。这意味着在整个训练过程中，学习率保持不变。这种策略简单易懂，但可能不适用于数据分布变化较大的情况。

与固定学习率相对的是动态学习率策略，其中学习率会根据训练进度或者性能表现进行调整。动态学习率能够更灵活地应对训练过程中遇到的各种挑战，如学习率预热、冷却、周期性调整等。

### 2.2.2 学习率衰减策略

学习率衰减是一种常见的动态学习率调整方法。其核心思想是在训练的早期阶段使用较大的学习率以加快学习速度，而在训练后期降低学习率，以使模型在收敛阶段更加稳定。衰减策略有多种实现方式，常见的包括步长衰减、指数衰减、余弦退火衰减等。

下面是一个指数衰减学习率的示例：

import numpy as np

initial_lr = 0.1
decay_rate = 0.96
decay_steps = 100

global_step = 0
lr = initial_lr

while global_step < number_of_epochs:
    lr = initial_lr * (decay_rate ** (global_step // decay_steps))
    global_step += 1
    update_parameters(lr)

在这个代码段中，我们使用指数衰减策略来逐渐减少学习率。通过这种方式，我们能够保证学习率在训练过程中适时地调整，以适应不同的阶段。

### 2.2.3 自适应学习率算法

自适应学习率算法是深度学习领域的一大突破，它们能够自动地调整学习率，使得训练过程更加高效。其中，最具代表性的是Adam、RMSprop等算法。这些算法通常能够跟踪每个参数的学习率，基于梯度的历史信息来调整学习率，因此对各种问题的适应性更强。

自适应学习率算法的核心是估计每个参数梯度的一阶矩估计（即梯度的均值）和二阶矩估计（即梯度的未中心化的方差），然后根据这些估计来调整参数的学习率。

接下来的章节将详细探讨学习率对神经网络训练的具体影响以及调整与优化策略。这将为理解学习率在深度学习中的关键作用奠定坚实的基础。

# 3. 学习率对神经网络训练的影响

学习率作为神经网络训练过程中的核心超参数，其对训练效果和模型性能有着深远的影响。本章节将详细探讨学习率如何影响梯度下降法，以及学习率与网络权重更新之间的关系。此外，还将讨论学习率选择不当可能导致的问题，以及如何通过调整学习率来改善模型的训练过程。

## 3.1 学习率与梯度下降法

### 3.1.1 学习率对收敛速度的影响

在神经网络训练中，梯度下降法是一种常见的优化算法，用于最小化损失函数。学习率决定了在每次迭代中模型参数调整的幅度。如果学习率设置得过高，模型可能无法收敛，甚至出现发散的情况。反之，学习率过低会使得训练过程非常缓慢，需要更多的迭代次数才能达到收敛，甚至可能陷入局部最小值。

为了更直观地理解学习率对收敛速度的影响，我们可以考虑以下的实验设计：

1. 选择一个标准数据集，例如MNIST手写数字识别数据集。
2. 使用一个简单的神经网络模型，比如两层的全连接网络。
3. 固定其他超参数，如批大小和迭代次数，分别使用不同的学习率进行训练。
4. 记录每个学习率下的收敛速度和收敛点。

实验结果可能会表明，存在一个最优的学习率区间，使得模型能够快速且稳定地收敛到一个较低的损失值。

### 3.1.2 学习率对模型泛化能力的影响

泛化能力是指模型在未见过的数据上的表现能力。学习率不仅影响训练过程的收敛速度，还会影响模型的泛化能力。如果学习率过高，模型可能会在训练数据上过拟合，无法很好地推广到新数据上。而过低的学习率可能导致欠拟合，模型不能捕捉到数据中的特征。

为了探讨学习率如何影响泛化能力，可以设计以下实验：

1. 在相同的训练数据集上训练模型，使用不同的学习率。
2. 在验证集上评估每个模型的性能，观察模型的泛化误差。

实验可能揭示出学习率与泛化误差之间的某种关系，例如存在一个学习率使得模型具有最佳的泛化性能。

## 3.2 学习率与网络权重更新

### 3.2.1 权重更新与学习率的关系

在神经网络中，权重更新是根据损失函数关于权重的梯度以及学习率来进行的。学习率决定了梯度更新步骤的大小。如果学习率太大，那么权重更新可能会跳过最优解；如果学习率太小，更新步子太小可能会导致训练过程陷入局部最优解。

为了深入理解权重更新与学习率的关系，我们可以推导出权重更新的公式：

# 假设权重为 w，学习率为 lr，损失函数关于权重的梯度为 grad
w = w - lr * grad

通过上述公式可知，学习率直接决定了权重更新的幅度。在实际应用中，为了能够清晰地分析学习率对权重更新的影响，可以设置不同的学习率值进行实验，并观察权重更新的历史变化。

### 3.2.2 学习率与梯度消失/爆炸问题

在深层神经网络中，梯度消失和梯度爆炸是常见的问题。学习率的不当设置可能会加剧这一问题。梯度消失意味着梯度值变得非常小，导致权重几乎不更新，使得网络难以学习到有效的特征。梯度爆炸则相反，梯度值过大，导致权重更新过大，破坏了网络结构的稳定性。

为了缓解梯度消失或爆炸的问题，可以采取以下几种策略：

1. 使用梯度剪切技术，限制梯度的最大值。
2. 应用权重初始化技巧，如He初始化或Xavier初始化。
3. 调整学习率，使用学习率衰减策略，使学习率在训练过程中逐渐减小。

下面是一个使用梯度剪切的代码示例：

import torch

# 假设 model 是一个 PyTorch