【学习率：深度剖析与实战优化】

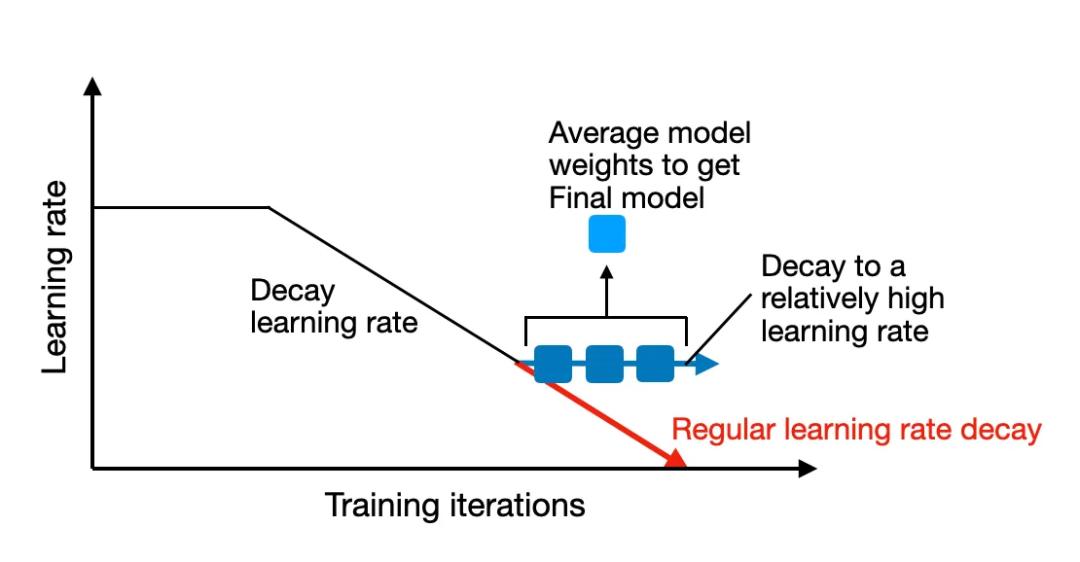
# 1. 学习率在机器学习中的重要性

在构建和训练机器学习模型的过程中，学习率是一个核心的超参数，它直接影响到模型训练的效率与最终效果。学习率决定了参数更新的步长，若步长过大，模型可能无法收敛，甚至发散；若步长过小，则会导致模型收敛速度过慢，训练过程耗时过长，还可能陷入局部最小值。在本章节中，我们将探索学习率在模型训练中的关键作用，以及如何通过调整学习率来优化机器学习工作流程。

## 学习率对模型性能的影响

学习率的调整直接关系到模型参数更新的准确性与速度，可以视为推动模型迭代进步的“速度控制器”。高学习率可能会让模型错过最佳的损失函数值，而低学习率则可能导致模型训练在达到可接受的性能前就因为资源或时间限制而终止。

## 学习率与优化算法的关系

在不同的优化算法中，学习率扮演的角色也有所不同。例如，在使用梯度下降算法时，学习率直接决定了每次迭代中参数的更新幅度。而在自适应学习率算法如Adam中，学习率的动态调整机制使得模型能够更好地适应不同的训练阶段。

# 2. 学习率的基础理论与公式解析

学习率是机器学习尤其是深度学习中的一个重要概念，它决定了在梯度下降过程中参数更新的步长。一个合适的学习率能够确保模型快速收敛并达到良好的性能，而一个不恰当的学习率则可能导致模型训练失败，表现为收敛速度慢、过拟合、欠拟合等问题。在本章中，我们将深入解析学习率的基础理论与公式，帮助读者更好地理解学习率的作用和如何进行选择与计算。

## 2.1 学习率的定义及其作用

学习率定义了模型权重更新的幅度大小，它在模型训练过程中起着至关重要的作用。理解学习率对于掌握机器学习算法至关重要。

### 2.1.1 学习率对模型训练的影响

学习率决定了在参数空间中，每次迭代时模型权重更新的幅度。一个高的学习率可能导致模型权重更新过大，从而使模型无法收敛或者在最优值附近振荡。相反，一个低的学习率可能使模型训练过程缓慢，甚至停滞不前。

在实际应用中，学习率的选择往往需要多次尝试和调整。过高的学习率会导致优化过程变得不稳定，甚至发散，而过低的学习率则会导致训练过程耗时过长，效率低下。

### 2.1.2 学习率在不同优化算法中的角色

不同的优化算法对学习率的依赖程度和反应各异。例如，SGD（随机梯度下降）算法对学习率的选择非常敏感，而像Adam这样的自适应学习率算法则可以通过算法内部的机制自动调整学习率。

学习率在不同优化算法中的角色具体表现为：

- 在SGD中，学习率直接控制了每次权重更新的步长。
- 在Momentum中，学习率与动量项共同决定了权重更新的方向和幅度。
- 在RMSprop和Adam中，学习率是通过算法内部的机制来动态调整的，这使得算法对学习率的选择不那么敏感。

## 2.2 学习率的理论模型

学习率的理论模型是基于数学推导和理论分析的，它帮助我们更好地理解学习率与模型优化之间的关系。

### 2.2.1 优化算法与学习率的关系

优化算法的设计初衷是为了高效且稳定地找到损失函数的最小值。学习率作为算法中的一个关键超参数，与优化算法的设计有着密不可分的联系。例如，动量项的设计在某种程度上就是为了缓解学习率选择不当带来的影响，而Adam算法中的自适应学习率机制更是直接针对学习率的动态调整进行了优化。

### 2.2.2 学习率衰减策略的理论基础

学习率衰减策略是随着训练的进行逐步减小学习率的方法，它基于这样的理论假设：随着模型接近最优参数，我们更希望模型在参数空间中的更新步长较小，以保证模型能够稳定地收敛到最优解。

学习率衰减策略有多种实现方式，如固定时间衰减、基于性能的衰减和周期性衰减等。这些策略需要根据具体问题和模型进行选择和调整。

## 2.3 学习率的计算方法

学习率的计算方法是实际应用中操作者需要重点关注的内容，合适的计算方法能够有效地提升模型的收敛速度和性能。

### 2.3.1 固定学习率的选择

固定学习率是最简单也是最常用的计算方法，它在训练开始之前设定一个固定值作为学习率。这个值通常通过经验或者超参数搜索来确定。例如，在一些简单任务中，学习率可能从0.01、0.001等常用值中选取。

一个固定的较低学习率虽然稳定，但可能会导致训练速度慢；而较高的学习率虽然可以加速收敛，但有可能导致收敛不稳定甚至发散。

### 2.3.2 自适应学习率算法的原理

自适应学习率算法通过算法内部的机制来动态调整每个参数的学习率。最著名的自适应学习率算法包括AdaGrad、RMSprop和Adam等。

以Adam算法为例，它结合了动量和学习率自适应调整的优势，通过计算梯度的一阶矩估计和二阶矩估计，分别对应于梯度的累积和梯度平方的累积，然后基于这两个估计来调整每个参数的学习率。这样，对于梯度变化不大的参数，Adam会采用较大的学习率；而对于梯度变化较大的参数，Adam则会采用较小的学习率，从而提高了模型训练的效率和稳定性。

# 伪代码展示Adam优化器的实现逻辑
for each weight in model_weights:
    # 计算梯度一阶矩估计(即动量)
    m = beta1 * m + (1 - beta1) * gradient
    # 计算梯度二阶矩估计
    v = beta2 * v + (1 - beta2) * (gradient ** 2)
    # 修正一阶矩估计的偏差
    m_hat = m / (1 - beta1 ** t)
    # 修正二阶矩估计的偏差
    v_hat = v / (1 - beta2 ** t)
    # 更新权重
    weight = weight - learning_rate * m_hat / (sqrt(v_hat) + epsilon)

在上述伪代码中，`beta1` 和 `beta2` 是控制动量项和梯度平方项衰减率的超参数，通常设为0.9和0.999；`epsilon` 是一个很小的数，用来避免除以0；`t` 是当前迭代的步数。通过这种方式，Adam算法能够自适应地调整每个参数的学习率。

通过本章节的介绍，我们深入了解了学习率的基础理论、计算方法和其在优化算法中的作用。学习率的选择与调整直接关系到模型训练的效率与最终性能，因此它是机器学习实践中不可忽视的关键因素。接下来的章节将探讨学习率的调整方法与实践经验，进一步指导我们在实际工作中的应用。

# 3. 学习率的调整方法与实践经验

### 3.1 学习率预热与学习率衰减
在深度学习的训练过程中，初始学习率的选择和调整策略对模型收敛速度和最终性能有着重要影响。学习率预热（learning rate warmup）和衰减（learning rate decay）是两种常用的调整方法。

#### 3.1.1 学习率预热的必要性
学习率预热是指在训练的初期阶段，将学习率从一个较小的值逐渐增加到预设的学习率。这种策略对于一些需要精细调整的大型模型特别重要。如果直接从一个较大的学习率开始训练，可能会因为梯度更新过大而导致权重初始化的破坏。通过预热，模型能够在早期阶段更加稳定地学习，有助于避免训练初期的不稳定行为。

以下是学习率预热的基本步骤：
1. 在训练开始时设置一个较小的学习率。
2. 在训练的前几个epoch逐渐增加学习率直到达到目标学习率。
3. 保持目标学习率不变进行后续的训练，直到满足停止条件。

# 伪代码示例展示学习率预热策略
global_step = 0
total_steps = 10000
warmup_steps = 500
base_lr = 0.01
warmup_lr = 0.001

for each batch in train_dataloader:
    # 计算当前的学习率
    current_lr = base_lr if global_step > warmup_steps else \
        warmup_lr + (base_lr - warmup_lr) * (global_step / warmup_steps)
    # 更新模型参数
    update_parameters(current_lr)
    # 更新全局步数
    global_step += 1

#### 3.1.2 学习率衰减的具体实现
学习率衰减通常在训练过程的某个时间点之后逐步减小学习率，以实现模型的精细调整。常见的衰减策略包括固定步长衰减、指数衰减和周期性衰减等。衰减策略有助于模型跳出局部最小值，提高收敛精度。

一个简单的固定步长衰减策略的实现如下：

# 伪代码示例展示固定步长学习率衰减策略
global_step = 0
total_steps = 10000
decay_factor = 0.1
decay_step = 500

for each batch in train_dataloader:
    # 原始学习率
    current_lr = 0.01
    # 如果达到衰减步数，则调整学习率
    if global_step > decay_step and global_step % decay_step == 0:
        current_lr *= decay_factor
    # 更新模型参数
    update_parameters(current_lr)
    # 更新全局步数
    global_step += 1

### 3.2 学习率范围的确定
在实践中，学习率的选择范围往往需要通过一系列的实验来确定，因为它很大程度上依赖于具体的任务和模型结构。

#### 3.2.1 超参数搜索策略
通过超参数搜索策略，如网格搜索、随机搜索或贝叶斯优化等方法，可以在学习率的可能范围内进行搜索，找到一个相对较好的学习率值。这些方法通常用于初始化学习率的选择，或者在衰减策略中确定衰减频率和衰减因子。

# 伪代码示例展示使用网格搜索方法确定学习率
best_loss = float('inf')
best_lr = 0.0
search_lr = [0.001, 0.01, 0.1, 1.0]

for lr in search_lr:
    # 使用当前学习率进行训练，并验证其性能
    loss = train_and_evaluate_model(lr)
    # 如果当前学习率对应的验证损失更低，则更新最佳学习率
    if loss < best_loss:
        best_loss = loss
        best_lr = lr

# 使用找到的最佳学习率进行进一步训练
train_model(best_lr)

#### 3.2.2 学习率范围的经验法则
尽管超参数搜索能帮助找到较好的学习率，但在没有足够资源进行大量搜索时，一些经验法则可以帮助我们确定学习率的起始值。一般来说，学习率的起始值应该足够大以保证模型能够学习，但同时又不能大到使模型训练不稳定。根据经验，一个常用的做法是将学习率初始化为0.01，然后根据训练过程中的损失下降情况对其进行调整。

### 3.3 学习率调整的高级技巧
随着深度学习技术的发展，一些高级技巧被提出以进一步优化学习率调整策略。

#### 3.3.1 循环学习率与周期性调整
循环学习率是一种较为新颖的调整策略，它在每个周期内改变学习率的值，通常学习率会在最大值和最小值之间周期性地变化。这种策略允许模型在一个周期内经历不同的学习率，从而可以在不同的训练阶段探索不同的权重空间，有助于模型跳出局部最小值。

# 伪代码展示循环学习率策略
global_step = 0
period = 1000
min_lr = 0.001
max_lr = 0.01

for each batch in train_dataloader:
    # 计算当前周期内的学习率
    cycle = np.floor(1 + global_step / (2 * period))
    x = np.abs(global_step / period - 2 * cycle + 1)
    current_lr = min_lr + (max_lr - min_lr) * max(0, (1 - x))  # triangle wave
    # 更新模型参数
    update_parameters(current_lr)
    # 更新全局步数
    global_step += 1

#### 3.3.2 基于验证集性能的学习率自动调整
在训练过程中，除了预设的学习率调整策略外，还可以根据模型在验证集上的性能动态调整学习率。具体方法包括当模型在验证集上的性能不再提升时降低学习率，或者在性能提升时保持当前学习率，直到性能再次下降。这样可以确保模型在训练过程中始终以最佳的学习率进行更新。

# 伪代码展示基于验证集性能的学习率调整策略
global_step = 0
best_val_loss = float('inf')
best_lr = 0.01
current_lr = best_lr

for each epoch in training:
    train_loss = train_one_epoch(current_lr)
    val_loss = validate_model()
    if val_loss < best_val_loss:
        # 如果验证集性能提升，保存最佳学习率
        best_val_loss = val_loss
        best_lr = current_lr
    else:
        # 如果验证集性能不再提升，则降低学习率
        current_lr *= 0.9
    # 更新模型参数
    update_parameters(current_lr)
    # 更新全局步数
    global_step += 1

以上就是学习率调整的实践经验，通过这些方法，我们可以更加精确地控制训练过程中的学习率变化，从而有效提升模型训练的稳定性和收敛性能。在下一节中，我们将探讨学习率的优化技术在深度学习中的应用。

# 4. 学习率的优化技术在深度学习中的应用

随着深度学习模型的复杂性日益增加，合理选择和优化学习率成为提高模型性能和训练效率的关键。在本章中，我们将探讨学习率优化技术在深度学习中的应用，分析在解决梯度消失和梯度爆炸问题中的作用，并深入讨论学习率调度策略和优化算法的实验与应用。

## 4.1 梯度消失与梯度爆炸的解决方案

梯度消失和梯度爆炸是在训练深层神经网络时常见的两个问题，它们直接影响模型的收敛速度和性能。学习率作为控制梯度更新幅度的关键超参数，在这两个问题的解决中扮演着重要角色。

### 4.1.1 学习率对梯度问题的影响

学习率的大小决定了在每次参数更新中梯度影响的大小。如果学习率过高，更新步骤可能过大，导致梯度爆炸问题；相反，如果学习率过低，更新步骤可能过小，导致梯度消失问题。因此，合理选择学习率是缓解这两个问题的重要手段。

在实践中，可以通过以下方式调整学习率以解决梯度问题：

- 使用自适应学习率优化算法（如Adam），它们能够自动调整学习率，有助于缓解梯度问题。
- 使用梯度裁剪技术，它能够限制梯度的大小，防止梯度爆炸。
- 通过规范化层（如Batch Normalization）来稳定训练过程，间接帮助解决梯度问题。

### 4.1.2 实战中梯度问题的处理技巧

在处理梯度消失和梯度爆炸时，除了上述提到的方法外，还有一些实用的技巧可以应用：

- **初始化权重**：使用合适的权重初始化方法（如He初始化、Xavier初始化）可以在一定程度上缓解梯度问题。
- **权重正则化**：在目标函数中加入L1或L2正则项有助于稳定梯度。
- **逐层正则化**：例如，ResNet的残差学习结构可以有效缓解梯度消失问题。

下面是一个简单的权重初始化的代码示例，展示了如何在PyTorch中实现He初始化：

import torch
import torch.nn as nn

def he_init(module):
    if isinstance(module, nn.Conv2d):
        nn.init.kaiming_normal_(module.weight, mode='fan_in', nonlinearity='relu')
    elif isinstance(module, nn.BatchNorm2d):
        nn.init.constant_(module.weight, 1)
        nn.init.constant_(module.bias, 0)

# 示例：创建一个简单的卷积层并应用He初始化
conv_layer = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1)
he_init(conv_layer)

该代码段首先定义了一个初始化函数`he_init`，然后创建了一个卷积层并对其权重应用了He初始化方法。这种初始化有助于在训练初期缓解梯度消失问题。

## 4.2 学习率调度的实验与分析

学习率调度是指在训练过程中动态调整学习率的技术。它可以帮助模型更快速地收敛，同时提高模型在验证集上的泛化性能。

### 4.2.1 不同调度策略的对比实验

在对比不同学习率调度策略时，常见的方法包括：

- **学习率预热**：在训练初期逐渐增加学习率，避免由于初始学习率过低导致的收敛缓慢。
- **学习率衰减**：在训练过程中逐渐减少学习率，以防止过拟合，并帮助模型在训练后期进行更细致的调整。
- **循环学习率**：周期性地调整学习率，允许模型在不同的学习率下探索更广泛的空间，有助于跳出局部最小值。

下面是一个使用PyTorch实现学习率预热和衰减的代码示例：

from torch.optim.lr_scheduler import LambdaLR

def lr_schedule(epoch):
    # 学习率预热：前5个epoch线性增加学习率，从0到初始学习率
    if epoch < 5:
        return epoch / 5
    # 学习率衰减：之后每个epoch乘以0.9
    else:
        return 0.9 ** epoch

optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = LambdaLR(optimizer, lr_lambda=lr_schedule)

# 训练循环中调用scheduler.step()来更新学习率
for epoch in range(num_epochs):
    # 训练和验证过程...
    scheduler.step()

该代码段定义了一个学习率调度函数`lr_schedule`，并在训练循环中通过调用`scheduler.step()`来更新学习率。

### 4.2.2 学习率调度对模型性能的影响分析

通过实验我们可以分析不同学习率调度策略对模型性能的影响。一般来说，学习率预热有助于模型在开始时快速学习，而学习率衰减则有助于模型在训练后期进行精细调整，从而改善模型的泛化能力。

下表展示了不同学习率调度策略在训练过程中的性能变化情况：

| 阶段 | 学习率预热 | 学习率衰减 |
|------|------------|------------|
| 初始阶段 | 有助于快速收敛 | 避免过拟合，逐步细化参数调整 |
| 中期阶段 | 维持稳定的学习速度 | 促进模型收敛 |
| 后期阶段 | 避免训练停滞 | 有助于获得更好的验证集性能 |

通过对比分析，我们可以得出结论，合适的调度策略能够显著提升模型的训练效率和最终性能。

## 4.3 学习率优化算法的深入探讨

在深度学习中，除了学习率调度策略外，还有多种优化算法可以直接调整学习率，比如梯度裁剪和正则化技术、动量以及自适应矩估计（Adam）算法。

### 4.3.1 梯度裁剪与正则化技术

梯度裁剪是一种通过限制梯度的大小来防止梯度爆炸的技术。例如，在反向传播时，如果梯度大于某个阈值，则将其裁剪到该阈值。以下是使用PyTorch实现梯度裁剪的代码示例：

torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

该代码片段使用`clip_grad_norm_`函数限制模型参数的梯度范数不超过1.0，以此来避免梯度爆炸的问题。

正则化技术（如L1和L2正则化）可以在损失函数中加入一个惩罚项，鼓励模型保持参数的稀疏性或较小的参数值，从而间接帮助缓解梯度问题。

### 4.3.2 动量与自适应矩估计（Adam）的原理与应用

动量（Momentum）和自适应矩估计（Adam）是两种广泛使用的自适应学习率优化算法。动量算法引入了动量概念，帮助加速学习过程，并在梯度方向一致时提供更大的更新步伐。Adam算法则结合了动量和RMSprop的思想，根据历史梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。

下面是一个使用Adam优化器的PyTorch示例代码：

optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999))

在这段代码中，我们使用了Adam优化器，并设置了动量参数`betas`。Adam优化器通过调整每个参数的学习率，使得模型在训练过程中能够更快速地收敛到损失函数的最小值。

通过上述讨论和示例代码，我们可以看到学习率优化技术在深度学习中的广泛应用，以及如何在实践中应用这些技术来提高模型性能和训练效率。

# 5. 学习率调优的实战案例分析

学习率调优是深度学习中的关键实践环节，直接影响到模型训练的效率和最终的性能表现。在本章节中，我们将深入分析学习率调优的实战应用，并探讨从简单到复杂的场景中学习率的具体应用。此外，我们还将提供专家级的建议和注意事项，帮助读者在实际工作中更好地实施学习率调优。

## 5.1 从简单到复杂的实战场景

### 5.1.1 线性回归模型的学习率优化

在机器学习的入门阶段，线性回归模型是最简单的模型之一。尽管其简单，但对学习率的理解和调优仍然至关重要。下面，我们将通过线性回归模型展示学习率的调优过程。

#### 实战步骤

1. **初始化参数**：首先，确定模型的初始参数，包括学习率、迭代次数等。
2. **模型训练**：使用随机梯度下降（SGD）等优化算法来更新参数。
3. **学习率调整**：通过观察模型的损失函数值，实时或周期性地调整学习率。
4. **评估与验证**：在验证集上评估模型性能，并根据性能结果进一步微调学习率。

#### 代码示例

import numpy as np
from sklearn.datasets import make_regression
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error

# 生成线性回归数据集
X, y = make_regression(n_samples=100, n_features=10, noise=0.1, random_state=42)

# 初始化线性回归模型，并设置学习率为0.01
model = SGDRegressor(learning_rate='constant', eta0=0.01)

# 训练模型
model.fit(X, y)

# 预测
y_pred = model.predict(X)

# 评估模型性能
mse = mean_squared_error(y, y_pred)
print(f'Mean Squared Error: {mse}')

#### 参数说明

- `eta0`：初始学习率，代表优化过程的步长。
- `mean_squared_error`：均方误差，用来评估模型的性能。

### 5.1.2 卷积神经网络的学习率调整实践

当模型复杂度增加，如使用卷积神经网络（CNN）进行图像识别任务时，学习率的调整变得更加重要。以下是针对CNN模型学习率调优的实战分析。

#### 实战步骤

1. **模型架构搭建**：使用深度学习框架构建CNN模型架构。
2. **超参数设定**：确定优化器、学习率、批次大小等超参数。
3. **学习率预热**：在训练初期逐渐增加学习率，以加速收敛。
4. **学习率衰减**：随着训练的进行，逐步减小学习率，以精细化模型参数。

#### 代码示例

from tensorflow.keras import layers, models
from tensorflow.keras.optimizers import Adam

# 构建CNN模型
model = models.Sequential([
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(64, (3, 3), activation='relu'),
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(64, (3, 3), activation='relu'),
    layers.Flatten(),
    layers.Dense(64, activation='relu'),
    layers.Dense(10, activation='softmax')
])

# 编译模型，设置初始学习率
model.compile(optimizer=Adam(learning_rate=0.001),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 训练模型，包含学习率预热和衰减策略
history = model.fit(train_images, train_labels, epochs=10, 
                    validation_data=(validation_images, validation_labels),
                    callbacks=[LearningRateScheduler(lambda epoch: 1e-3 * 0.9**epoch)])

#### 参数说明

- `Conv2D`：卷积层，用于提取图像特征。
- `MaxPooling2D`：池化层，用于降低特征维度。
- `Dense`：全连接层，用于分类。
- `Adam`：自适应矩估计优化器，根据梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
- `LearningRateScheduler`：回调函数，用于学习率的周期性调整。

## 5.2 学习率调优的进阶应用

### 5.2.1 复杂网络结构中的学习率应用

在处理复杂网络结构，比如循环神经网络（RNN）、长短期记忆网络（LSTM）以及复杂的注意力机制网络时，学习率调优策略将更为关键。

#### 实战分析

- **梯度爆炸问题**：在RNN类模型中，长序列的训练可能会导致梯度爆炸问题，此时需要合理设置学习率以避免此问题。
- **跨层学习率调整**：不同层次的网络可能需要不同的学习率，自适应学习率优化算法（如Adam）能够有效解决这一问题。

### 5.2.2 大规模数据集上的学习率优化策略

在大规模数据集上训练时，我们面临着计算资源的限制和模型收敛速度的挑战。合理的学习率调整策略能够帮助我们更有效地利用资源。

#### 实战分析

- **分布式训练**：在分布式训练场景下，学习率应根据不同的计算节点进行调整。
- **学习率预热与尾部衰减**：在训练的初期，通过预热学习率加速模型学习，在训练的后期，通过尾部衰减精细化模型参数。

## 5.3 学习率优化的注意事项与建议

### 5.3.1 避免常见错误与陷阱

在学习率调优过程中，一些常见错误和陷阱需要引起注意：

- **学习率过高或过低**：过高的学习率可能导致模型无法收敛，过低的学习率则会使训练变得异常缓慢。
- **未考虑数据特征**：不同特征和规模的数据集对学习率的要求不同，应根据实际情况调整。
- **忽视学习率的动态调整**：静态的学习率可能不适应整个训练过程，动态调整学习率对性能提升至关重要。

### 5.3.2 专家建议与调优最佳实践

以下是一些专家建议的学习率调优最佳实践：

- **始终监控**：在训练过程中密切关注学习率对模型性能的影响。
- **使用预训练模型**：利用预训练模型作为起点，可以有效地缩小学习率的搜索范围。
- **采用学习率调度策略**：周期性地调整学习率能够帮助模型更好地收敛。

通过本章节的深入分析，我们可以看到学习率调优在实际应用中的重要性以及如何根据不同的模型和数据集进行有效的学习率调优。在接下来的章节中，我们将探讨学习率调优的自动化工具，以及学习率研究的最新动态。

# 6. 学习率调优的工具与未来趋势

## 6.1 学习率调优的自动化工具

在机器学习和深度学习的实践中，学习率的调优往往需要大量的尝试和实验，因此，自动化学习率调优工具的发展显得尤为重要。通过减少人工干预，这些工具能够在较短的时间内找到最优的学习率设置。

### 6.1.1 自动学习率选择的框架

目前，一些主流的深度学习框架已经开始集成学习率调度器，这些调度器能够在训练过程中自动调整学习率。例如，在PyTorch中，`torch.optim.lr_scheduler`提供了多种学习率调度策略。用户可以通过简单的接口调用来实现学习率的自动调整。

import torch.optim as optim
from torch.optim.lr_scheduler import StepLR

optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
scheduler = StepLR(optimizer, step_size=30, gamma=0.1)

for epoch in range(1, 100):
    train(...)
    validate(...)
    scheduler.step()  # 调用该方法可以逐步降低学习率

### 6.1.2 调优工具在实际工作中的应用案例

自动化工具如Hyperopt、Optuna等已经广泛应用于机器学习实践中。它们通过定义一个搜索空间，在其中进行随机或基于贝叶斯优化的搜索，以找到最优的学习率及其他超参数配置。以Optuna为例，它能够结合模型验证的性能反馈，智能地指导参数搜索的方向。

下面是一个使用Optuna进行学习率自动调优的简单示例：

import optuna
import torch
import torch.nn as nn
from torch.optim import Adam

def objective(trial):
    # 定义搜索空间
    lr = trial.suggest_loguniform('lr', 1e-5, 1e-1)
    # 定义模型、损失函数和优化器
    model = ...  # 模型定义
    criterion = nn.CrossEntropyLoss()
    optimizer = Adam(model.parameters(), lr=lr)

    for epoch in range(50):  # 50个训练周期
        train_loss = ...
        val_loss = ...
        trial.report(val_loss, epoch)
        if trial.should_prune():
            raise optuna.exceptions.TrialPruned()

    return val_loss

study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)

print('最优的学习率为: {}'.format(study.best_params['lr']))

## 6.2 学习率研究的前沿动态

随着深度学习领域的不断发展，学习率的研究也在不断进步，新的理论和实践方法层出不穷，使得学习率的调优更加科学和高效。

### 6.2.1 学习率理论的最新进展

近年来，学者们对学习率的研究已经从简单的固定值或衰减策略，发展到了考虑训练阶段的学习率动态变化，以及与训练进度密切相关的自适应学习率算法。其中，基于梯度范数的学习率调度策略、循环学习率等方法都在实际应用中表现出色。

### 6.2.2 预期的学习率优化技术发展趋势

未来的研究可能会更加关注学习率的动态调整和个性化设置。例如，可能会开发出能够根据模型当前状态（如梯度的方差、参数的更新幅度等）动态调整学习率的算法。此外，如何在不同的优化算法中实现学习率的自适应调整，也是一个值得探讨的方向。

## 6.3 总结与展望

在深度学习领域，学习率的调整是一个永恒的话题。虽然已有诸多工具和方法能够辅助完成这项工作，但寻找最优的学习率仍然是一个复杂且具有挑战性的过程。

### 6.3.1 学习率调优的综合评价

学习率的调优涉及到对模型、数据以及优化算法深刻的理解。通过使用自动化工具和策略，可以显著减轻工程师的负担，使得学习率的调整更加高效和精确。同时，随着研究的深入，自适应学习率算法正在成为主流，并在许多情况下已经超越了传统的人工调整方法。

### 6.3.2 对未来研究方向的思考与建议

未来，学习率的研究将可能围绕以下几个方向展开：开发更加智能和灵活的自适应学习率算法；结合特定模型架构或数据集特性，提出更加高效的调优策略；以及通过实验和理论分析，进一步深化我们对学习率作用机制的理解。

这些发展方向不仅对学术界有着重要的意义，对实际工程问题的解决也有着深远的影响。随着研究的深入，我们可以期待学习率调优技术将在未来的机器学习实践中扮演更加关键的角色。