最小生成树的分析过程：从问题建模到算法实现，掌握算法设计思维

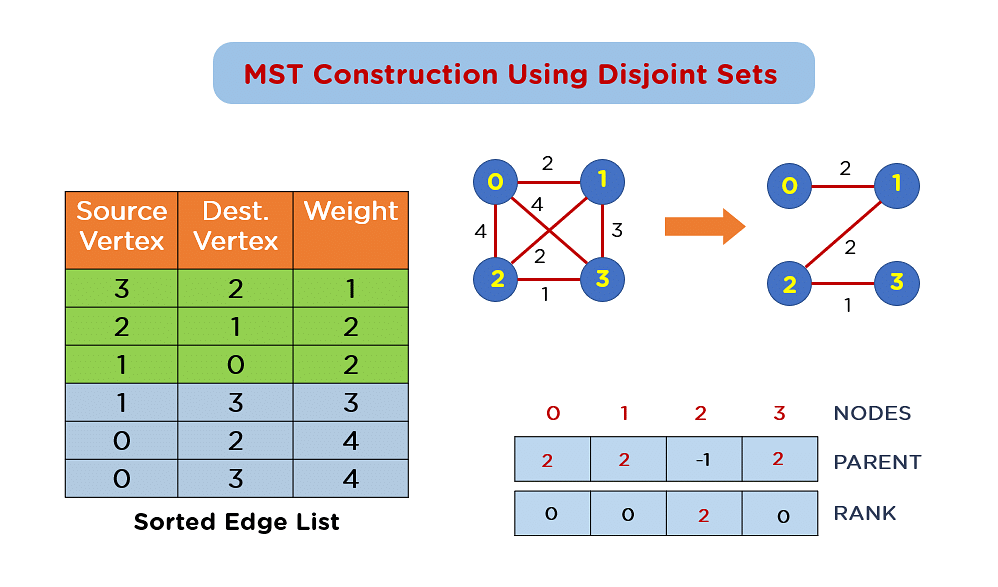
# 1. 最小生成树问题概述

最小生成树问题是图论中一个经典问题，它旨在寻找一个连接图中所有顶点的生成树，使得树中边的权重之和最小。生成树是指一个无环且包含图中所有顶点的连通子图。

最小生成树问题在实际应用中非常广泛，如网络规划、数据结构和图像处理等。例如，在网络规划中，最小生成树可以用于优化网络拓扑，以最小化网络延迟和成本。在数据结构中，最小生成树可以用于实现并查集和邻接表等数据结构。

# 2. 最小生成树算法理论基础

### 2.1 最小生成树的数学模型

#### 2.1.1 图论基础知识

**图的定义：**

图 G = (V, E) 由顶点集合 V 和边集合 E 组成，其中 V 是非空有限集合，E 是 V 上的二元关系。

**无向图：**

如果 E 中的边无方向，则 G 是无向图。

**有向图：**

如果 E 中的边有方向，则 G 是有向图。

**边的权重：**

每个边 e ∈ E 都可以赋予一个非负实数权重 w(e)。

**连通图：**

如果图 G 中任意两个顶点 u 和 v 之间都存在一条路径，则 G 是连通图。

#### 2.1.2 最小生成树的定义和性质

**最小生成树（MST）：**

对于一个连通无向加权图 G，其最小生成树 T 是一个连通无向子图，满足以下条件：

* T 包含 G 中所有顶点。
* T 中边的权重之和最小。

**MST 的性质：**

* MST 唯一。
* MST 中的边数为 |V| - 1。
* MST 中的任何环上的边权重之和都大于等于 MST 中对应边的权重之和。

### 2.2 最小生成树算法的分类

#### 2.2.1 贪心算法

**贪心算法：**

贪心算法是一种逐步构建解决方案的算法，在每一步中，算法都会做出局部最优的选择，希望最终得到全局最优解。

**克鲁斯卡尔算法：**

克鲁斯卡尔算法是一种贪心算法，它通过以下步骤构建 MST：

1. 初始化一个空图 T。
2. 将 G 中所有边按权重从小到大排序。
3. 对于每条边 e，如果 e 不形成 T 中的环，则将 e 加入 T。

**普里姆算法：**

普里姆算法也是一种贪心算法，它通过以下步骤构建 MST：

1. 选择一个顶点作为起始顶点，并将其加入 MST。
2. 对于 MST 中的每个顶点，找到权重最小的边连接到 MST 之外的顶点，并将其加入 MST。

#### 2.2.2 分治算法

**分治算法：**

分治算法是一种将问题分解为较小子问题的算法，然后递归地求解这些子问题，最后将子问题的解合并得到问题的解。

**Borůvka 算法：**

Borůvka 算法是一种分治算法，它通过以下步骤构建 MST：

1. 初始化一个包含所有顶点的森林 F。
2. 对于每个连通分量 C，找到 C 中权重最小的边 e，并将其加入 F。
3. 合并所有包含 e 端点的连通分量。
4. 重复步骤 2-3，直到 F 中只有一个连