最小生成树的应用：网络优化与数据聚类，掌握计算机科学中的实用算法

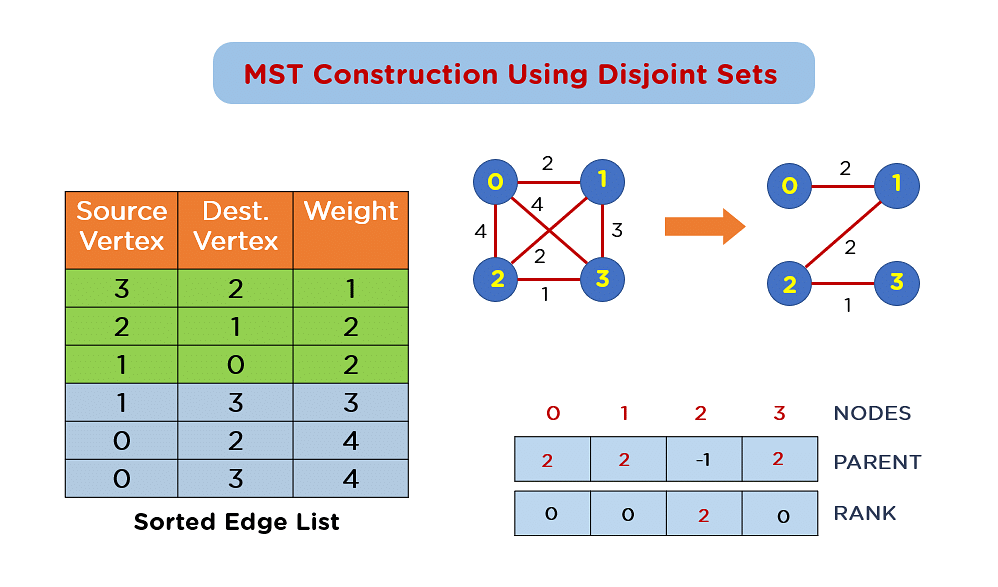
# 1. 最小生成树的概念和算法**

最小生成树（MST）是一种无向连通图中连接所有顶点的边集，其权值之和最小。MST在网络优化、数据聚类和其他领域有着广泛的应用。

**构造MST的算法**

有两种经典算法可以构造MST：普里姆算法和克鲁斯卡尔算法。普里姆算法从一个顶点出发，逐步添加权值最小的边，直到连接所有顶点。克鲁斯卡尔算法则从所有边出发，按权值从小到大排序，逐步合并无环子图，直到形成MST。

**算法复杂度**

普里姆算法和克鲁斯卡尔算法的时间复杂度均为O(E log V)，其中E是边数，V是顶点数。

# 2. 最小生成树在网络优化中的应用**

**2.1 网络拓扑结构与最小生成树**

网络拓扑结构是指网络中节点和链路的连接方式。最小生成树（MST）是一种特殊的生成树，它连接网络中的所有节点，同时总链路权重最小。在网络优化中，MST可以用于解决以下问题：

* **网络连通性：**MST确保网络中所有节点都相互连接，从而保证网络的连通性。
* **带宽优化：**MST选择总链路权重最小的生成树，从而优化网络的带宽利用率。
* **网络可靠性：**MST通过选择冗余路径，提高网络的可靠性，防止单点故障导致网络中断。

**2.2 最小生成树的算法实现**

有两种经典的MST算法：普里姆算法和克鲁斯卡尔算法。

**2.2.1 普里姆算法**

普里姆算法是一种贪心算法，它从一个节点开始，逐步扩展生成树，每次选择权重最小的边将新节点添加到生成树中。

def prim(graph):
    """
    普里姆算法实现最小生成树

    参数：
        graph: 图的邻接矩阵

    返回：
        最小生成树的边集
    """
    n = len(graph)
    visited = [False] * n
    mst = []

    # 从第一个节点开始
    visited[0] = True

    # 循环直到所有节点都被访问
    while not all(visited):
        # 找到权重最小的边
        min_weight = float('inf')
        min_edge = None
        for i in range(n):
            if visited[i]:
                for j in range(n):
                    if not visited[j] and graph[i][j] > 0 and graph[i][j] < min_weight:
                        min_weight = graph[i][j]
                        min_edge = (i, j)

        # 将权重最小的边添加到生成树中
        mst.append(min_edge)
        visited[min_edge[1]] = True

    return mst

**2.2.2 克鲁斯卡尔算法**

克鲁斯卡尔算法也是一种贪心算法，它从所有边开始，逐步合并生成树，每次选择权重最小的边，只要该边不会形成回路。

def kruskal(graph):
    """
    克鲁斯卡尔算法实现最小生成树

    参数：
        graph: 图的邻接矩阵

    返回：
        最小生成树的边集
    """
    n = len(graph)
    edges = []

    # 将所有边添加到边集中
    for i in range(n):
        for j in range(i + 1, n):
            if graph[i][j] > 0:
                edges.append((i, j, graph[i][j]))

    # 对边集按权重排序
    edges.sort(key=lambda edge: edge[2])

    # 初始化并查集
    parent = [i for i in range(n)