最小生成树的性能优化：提升效率和准确性，打造高性能算法

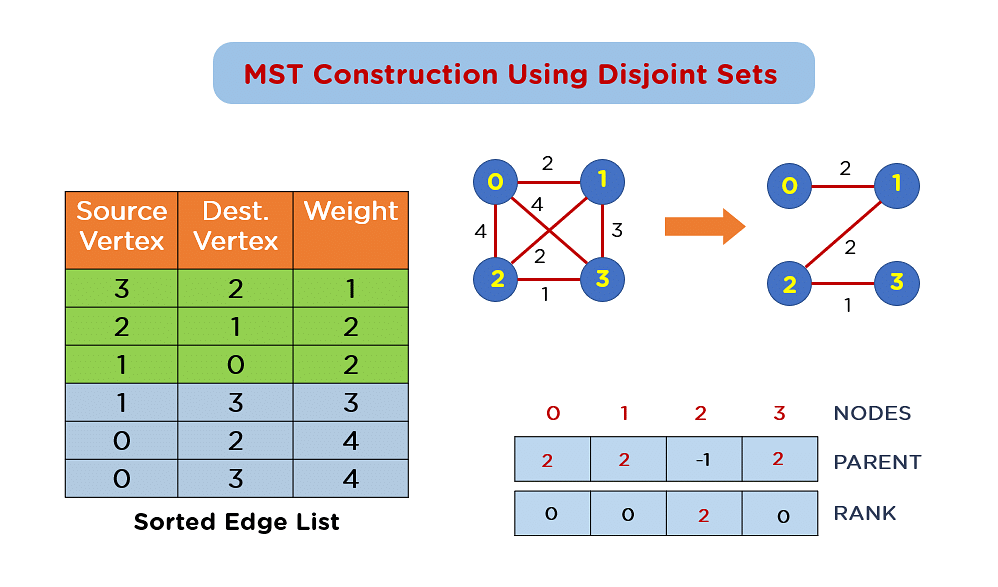
# 1. 最小生成树算法概述**

最小生成树（MST）算法是一种贪心算法，用于在连通图中找到一个包含所有顶点的子图，使得子图中的边权重和最小。MST算法在网络拓扑优化、图形处理和数据挖掘等领域有着广泛的应用。

MST算法的基本思想是，从一个顶点开始，逐步添加权重最小的边，直到所有顶点都被包含在生成树中。常见的MST算法包括Prim算法和Kruskal算法，它们都具有时间复杂度为O(E log V)，其中E是图中的边数，V是图中的顶点数。

# 2. 最小生成树算法性能优化

### 2.1 算法选择与比较

#### 2.1.1 Prim算法与Kruskal算法

最小生成树算法主要有Prim算法和Kruskal算法两种。Prim算法从一个顶点开始，逐步添加权重最小的边，直到生成一个生成树。Kruskal算法则先将所有边按权重从小到大排序，然后依次添加边，直到生成一个生成树。

**Prim算法**

def prim(graph, start_vertex):
    # 初始化
    visited = set()
    visited.add(start_vertex)
    pq = [(0, start_vertex)]  # (权重, 顶点)

    # 循环，直到所有顶点都被访问
    while pq:
        # 取出权重最小的边
        weight, vertex = heapq.heappop(pq)

        # 如果顶点已访问，则跳过
        if vertex in visited:
            continue

        # 否则，将顶点标记为已访问，并更新优先队列
        visited.add(vertex)
        for neighbor, weight in graph[vertex].items():
            if neighbor not in visited:
                heapq.heappush(pq, (weight, neighbor))

    # 返回最小生成树
    return visited

**Kruskal算法**

def kruskal(graph):
    # 初始化
    edges = []
    for vertex in graph:
        for neighbor, weight in graph[vertex].items():
            edges.append((weight, vertex, neighbor))

    # 对边进行排序
    edges.sort(key=lambda x: x[0])

    # 初始化并查集
    dsu = DisjointSetUnion()
    for vertex in graph:
        dsu.make_set(vertex)

    # 循环，直到所有边都被处理
    mst = []
    for weight, vertex1, vertex2 in edges:
        # 如果两个顶点不在同一个集合中，则添加边到最小生成树
        if dsu.find_set(vertex1) != dsu.find_set(vertex2):
            mst.append((weight, vertex1, vertex2))
            dsu.union(vertex1, vertex2)

    # 返回最小生成树
    return mst

#### 2.1.2 算法复杂度分析

| 算法 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| Prim算法 | O(E log V) | O(V + E) |
| Kruskal算法 | O(E log E) | O(V + E) |

其中，V表示图中的顶点数，E表示图中的边数。

从复杂度分析可以看出，Prim算法的时间复杂度与图的边数成正比，而Kruskal算法的时间复杂度与图的边数的对数成正比。因此，当图中边数较少时，Prim算法更优，而当图中边数较多时，Kruskal算法更优。

### 2.2 数据结构优化

#### 2.2.1 并查集的