算法爱好者探索：最小生成树的算法之美，深入理解算法的奥秘

# 1. 最小生成树概述

最小生成树（MST）是一种算法，用于在给定的加权无向图中找到一个包含所有顶点的生成树，且该生成树的边权和最小。MST在网络优化、交通规划和图像分割等领域有着广泛的应用。

最小生成树算法有两种主要类型：克鲁斯卡尔算法和普里姆算法。克鲁斯卡尔算法从所有边中选择权重最小的边，并逐步将这些边添加到生成树中，直到所有顶点都被连接起来。普里姆算法从一个顶点开始，并逐步将权重最小的边添加到生成树中，直到所有顶点都被连接起来。

# 2. 最小生成树算法理论基础

### 2.1 克鲁斯卡尔算法

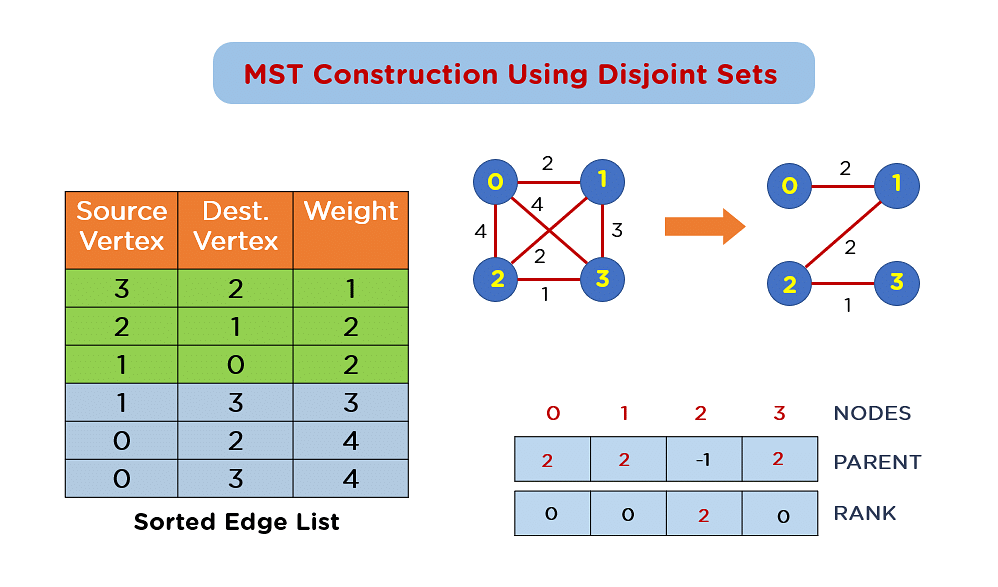
#### 2.1.1 算法原理

克鲁斯卡尔算法是一种贪心算法，用于寻找无向连通图中的最小生成树。该算法的基本思想是：

1. 将图中的所有边按权重从小到大排序。
2. 从权重最小的边开始，逐个添加到生成树中。
3. 如果添加的边不会形成环，则将其加入生成树；否则，丢弃该边。

#### 2.1.2 算法实现

def kruskal(graph):
    """
    克鲁斯卡尔算法实现最小生成树

    参数：
        graph: 无向连通图，以邻接表形式表示

    返回：
        最小生成树的边集
    """

    # 初始化并查集
    disjoint_set = DisjointSet()
    for vertex in graph:
        disjoint_set.make_set(vertex)

    # 将边按权重排序
    edges = sorted(graph.edges(), key=lambda edge: edge.weight)

    # 逐个添加边
    mst = []
    for edge in edges:
        u, v = edge.endpoints
        if disjoint_set.find_set(u) != disjoint_set.find_set(v):
            mst.append(edge)
            disjoint_set.union(u, v)

    return mst

**参数说明：**

* `graph`：无向连通图，以邻接表形式表示。

**代码逻辑逐行解读：**

1. 初始化并查集 `disjoint_set`，将图中的每个顶点作为并查集中的一个集合。
2. 将图中的边按权重从小到大排序，存储在 `edges` 列表中。
3. 逐个遍历 `edges` 列表中的边。
4. 对于每条边，获取其两个端点 `u` 和 `v`。
5. 使用并查集的 `find_set` 方法查找 `u` 和 `v` 所在的集合。
6. 如果 `u` 和 `v` 不在同一个集合中，则说明添加这条边不会形成环，将其添加到最小生成树 `mst` 中。
7. 使用并查集的 `union` 方法将 `u` 和 `v` 所在的集合合并。
8. 返回最小生成树 `mst` 中的边集。

### 2.2 普里姆算法

#### 2.2.1 算法原理

普里姆算法也是一种贪心算法，用于寻找无向连通图中的最小生成树。该算法的基本思想是：

1. 选择一个顶点作为生成树的根。
2. 从根顶点开始，逐个添加权重最小的边，将新的顶点添加到生成树中。
3. 如果添加的边不会形成环，则将其加入生成树；否则，丢弃该边。

#### 2.2.2 算法实现

def prim(graph, root):
    """
    普里姆算法实现最小生成树

    参数：
        graph: 无向连通图，以邻接表形式表示
        root: 生成树的根顶点

    返回：
        最小生成树的边集
    """

    # 初始化优先队列
    pq = PriorityQueue()
    for vertex in graph:
        if vertex != root:
            pq.add((vertex, root), float('inf'))

    # 初始化最小生成树
    mst = []

    # 从根顶点开始
    pq.add((root, None), 0)

    while not pq.is_empty():
        # 获取权重最小的边
        edge = pq.pop()
        u, v = edge.endpoints
        weight = edge.weight

        # 如果添加的边不会形成环，则将其加入生成树
        if v not in mst:
            mst.append(edge)

            # 将 v 的所有边加入优先队列