最小生成树：算法、应用与实战解析，掌握数据结构与算法的精髓

# 1. 最小生成树概述**

最小生成树（MST）是一种无向连通图中连接所有顶点的边集合，使得这些边的权重之和最小。它在网络优化、数据聚类和图论等领域有着广泛的应用。

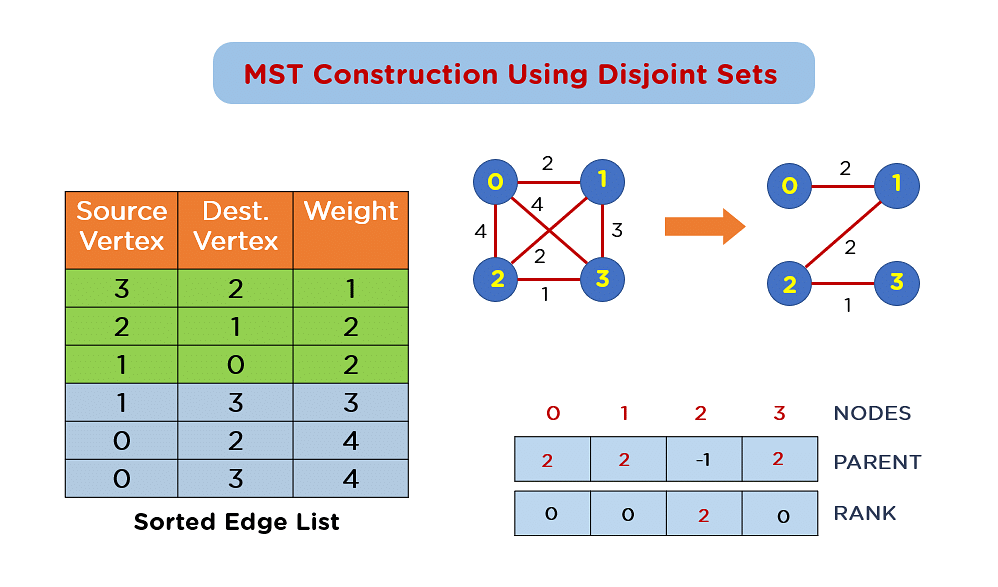
MST的构造过程是从图中选取一条权重最小的边作为初始边，然后依次添加权重最小的边，直到所有顶点都被连接起来。这个过程保证了最终得到的边集合具有最小的权重和。

MST的性质包括：

* 每个连通分量只有一个MST。
* MST中边的数量等于顶点数量减一。
* MST中的边权重之和等于图中所有边的权重之和的最小值。

# 2. 最小生成树算法

### 2.1 Prim算法

#### 2.1.1 算法原理

Prim算法是一种贪心算法，它从一个顶点开始，逐步扩展生成树，直到包含所有顶点。算法的步骤如下：

1. 选择一个顶点作为根节点。
2. 找到根节点到所有其他顶点的最短边。
3. 将最短边添加到生成树中。
4. 将最短边的终点添加到生成树中。
5. 重复步骤2-4，直到生成树包含所有顶点。

#### 2.1.2 算法实现

def prim(graph):
    """
    Prim算法实现最小生成树

    参数：
        graph: 图的邻接矩阵

    返回：
        最小生成树的边集
    """

    # 初始化生成树
    mst = set()

    # 初始化未访问顶点集
    unvisited = set(range(len(graph)))

    # 选择一个顶点作为根节点
    root = unvisited.pop()

    # 循环直到所有顶点都被访问
    while unvisited:
        # 找到根节点到所有未访问顶点的最短边
        min_edge = None
        for v in unvisited:
            if graph[root][v] < graph[root][min_edge] or min_edge is None:
                min_edge = v

        # 将最短边添加到生成树中
        mst.add((root, min_edge))

        # 将最短边的终点添加到生成树中
        unvisited.remove(min_edge)

        # 更新根节点
        root = min_edge

    return mst

**代码逻辑逐行解读：**

* **第5行：**初始化生成树为空集。
* **第7行：**初始化未访问顶点集为图中所有顶点的集合。
* **第9行：**选择一个顶点作为根节点，并将其从未访问顶点集中移除。
* **第12-18行：**循环直到所有顶点都被访问。
* **第13-16行：**找到根节点到所有未访问顶点的最短边。
* **第17行：**将最短边添加到生成树中。
* **第18行：**将最短边的终点添加到生成树中。
* **第19行：**更新根节点为最短边的终点。

### 2.2 Kruskal算法

#### 2.2.1 算法原理

Kruskal算法也是一种贪心算法，它从所有边开始，逐步合并生成树，直到包含所有顶点。算法的步骤如下：

1. 将所有边按权重从小到大排序。
2. 从权重最小的边开始，依次检查每条边。
3. 如果边的两个端点不在同一个连通分量中，则将边添加到生成树中。
4. 重复步骤3，直到生成树包含所有顶点。

#### 2.2.2 算法实现

def kruskal(graph):
    """
    Kruskal算法实现最小生成树

    参数：
        graph: 图的邻接矩阵

    返回：
        最小生成树的边集
    """

    # 初始化生成树
    mst = set()

    # 初始化连通分量
    components = {v: v for v in range(len(graph))}

    # 将所有边按权重从小到大排序
    edges = sorted(range(len(graph)), key=lambda e: graph[e[0]][e[1]])

    # 循环直到所有顶点都被访问
    while len(mst) < len(graph) - 1:
        # 取权重最小的边
        edge = edges.pop(0)

        # 如果边的两个端点不在同一个连通分量中
        if components[edge[0]] != components[edge[1]]:
            # 将边添加到生成树中
            mst.add(edge)

            # 合并边的两个端点的连通分量
            components = {v: components[edge[1]] if components[v] == components[edge[0]] else components[v] for v in range(len(graph))}

    return mst

**代码逻辑逐行解读：**

* **第5行：**初始化生成树为空集。
* **第7行：**初始化连通分量，每个顶点 initially 属于自己的连通分量。
* **第9行：**将所有边按权重从小到大排序。
* **第12-18行：**循环直到生成树包含所有顶点。
* **第13行：**取权重最小的边。
* **第14-17行：**如果边的两个端点不在同一个连通分量中，则将边添加到生成树中。
* **第18行：**合并边的两个端点的连通分量。

# 3. 最小生成树应用

### 3.1 网络拓扑优化

#### 3.1.1 网络拓扑结构

网络拓扑结构是指网络中节点和链路之间的连接方式。它决定了网络的连通性、可靠性和效率。常见的网络拓扑结构包括：

- **总线型拓扑：**所有节点连接到一条共享的总线，数据通过总线传输。
- **星型拓扑：**所有节点连接到一个中央交换机或集线器，数据通过交换机或集线器转发。
- **环形拓扑：**所有节点连接成一个环，数据沿环形路径传输。
- **网状拓扑：**所有节点相互连接，形成一个网状结构。

#### 3.1.2 最小生成树的应用

最小生成树算法可以用于优化网络拓扑结构，以最小化网络的总成本或最大化网络的连通性。具体来说，最小生成树算法可以用于：

- **最小成本网络设计：**给定一组节点和连接这些节点的成本，最小生成树算法可以找到连接所有节点的最低成本网络拓扑结构。
- **最大连通性网络设计：**给定一组节点和连接这些节点的可靠性，最小生成树算法可以找到连接所有节点的最大连通性网络拓扑结构。

### 3.2 数据聚类

#### 3.2.1 数据聚类概念

数据聚类是一种将数据点分组为具有相似特征的组的过程。聚类算法旨在找到具有高内聚度和低分离度的组。内聚度是指组内数据点的相似性，而分离度是指组间数据点的差异性。

#### 3.2.2 最小生成树在数据聚类中的应用

最小生成树算法可以用于数据聚类，通过将数据点视为节点，将数据点之间的相似性视为边权重来构建一个加权图。然后，使用最小生成树算法找到连接所有数据点的最低成本树。树中的连通分量对应于数据聚类的簇。

**示例：**

考虑以下数据点：

A = [1, 2]
B = [3, 4]
C = [5, 6]
D = [7, 8]

使用欧氏距离作为相似性度量，构建一个加权图：

       A     B     C     D
A  0.0   2.83  4.47  5.66
B  2.83  0.0   2.24  3