广度优先搜索算法及队列的关联性

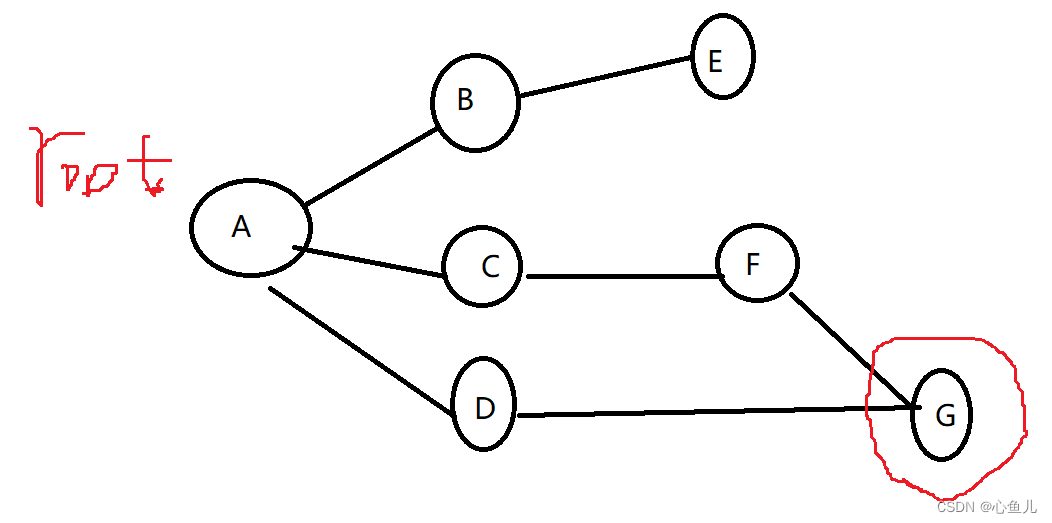
# 1. 广度优先搜索算法概述**

广度优先搜索（BFS）是一种遍历图或树的数据结构的算法。它以一种“广度优先”的方式工作，这意味着它首先访问当前节点的所有相邻节点，然后再继续访问更深层的节点。

BFS算法通常使用队列数据结构来存储要访问的节点。队列是一种先进先出的数据结构，这意味着最早进入队列的节点将最早被访问。这确保了BFS算法以广度优先的方式遍历图或树。

# 2. 队列数据结构与广度优先搜索

### 2.1 队列的定义和基本操作

#### 2.1.1 队列的先进先出特性

队列（Queue）是一种遵循先进先出（FIFO）原则的数据结构。这意味着最早进入队列的元素将首先被移除。队列的这种特性使其在各种应用中非常有用，例如：

* **消息传递：**队列用于存储待处理的消息，确保消息按顺序得到处理。
* **任务调度：**队列用于存储待执行的任务，任务按照先入先出的顺序被执行。
* **资源管理：**队列用于存储可用的资源，资源按照先入先出的顺序被分配。

#### 2.1.2 队列的实现方式

队列可以通过多种方式实现，最常见的两种实现方式是：

* **数组队列：**使用数组来存储队列中的元素。入队操作在数组末尾添加元素，出队操作从数组开头移除元素。
* **链表队列：**使用链表来存储队列中的元素。入队操作在链表尾部添加元素，出队操作从链表头部移除元素。

### 2.2 广度优先搜索算法的原理

#### 2.2.1 算法流程和伪代码

广度优先搜索（BFS）算法是一种遍历图或树的数据结构的算法。BFS算法遵循以下流程：

1. 从起始节点开始，将其放入队列中。
2. 循环执行以下步骤，直到队列为空：
- 从队列中取出队首元素。
- 访问队首元素。
- 将队首元素的所有未访问的相邻节点放入队列中。

#### 2.2.2 算法的时间复杂度和空间复杂度

BFS算法的时间复杂度取决于图或树的结构。对于一个具有V个节点和E条边的图，BFS算法的时间复杂度为O(V+E)。

BFS算法的空间复杂度取决于队列中存储的节点数量。最坏情况下，队列中可能存储所有节点，因此空间复杂度为O(V)。

### 代码示例

以下是用Python实现的BFS算法：

def bfs(graph, start):
    """
    广度优先搜索算法

    参数：
        graph：图的邻接表表示
        start：起始节点
    """

    # 初始化队列
    queue = [start]

    # 标记已访问的节点
    visited = set()

    # 循环执行BFS算法
    while queue:
        # 从队列中取出队首元素
        node = queue.pop(0)

        # 访问队首元素
        print(node)

        # 标记已访问
        visited.add(node)

        # 将队首元素的所有未访问的相邻节点放入队列中
        for neighbor in graph[node]:
            if neighbor not in visited:
                queue.append(neighbor)

### 代码逻辑分析

代码首先初始化一个队列，并将起始节点放入队列中。然后，代码进入一个循环，直到队列为空。在循环中，代码从队列中取出队首元素，访问该元素，并将其标记为已访问。接下来，代码将队首元素的所有未访问的相邻节点放入队列中。

### 参数说明

* `graph`：图的邻接表表示。
* `start`：起始节点。

# 3. 广度优先搜索算法在图论中的应用

### 3.1 图的表示和广度优先搜索

#### 3.1.1 图的邻接表和邻接矩阵

图是一种数据结构，用于表示对象之间的关系。在图论中，图由两个集合组成：顶点集合和边集合。顶点表示对象，边表示对象之间的关系。

图的表示方式主要有两种：邻接表和邻接矩阵。

**邻接表**：
- 使用一个数组来存储顶点，数组的每个元素是一个链表，链表中存储与该顶点相邻的顶点。
- 优点：存储空间小，适合稀疏图。
- 缺点：查找相邻顶点效率低。

**邻接矩阵**：
- 使用一个二维数组来存储顶点之间的关系，数组的每个元素表示两个顶点之间是否存在边。
- 优点：查找相邻顶点效率高。
- 缺点：存储空间大，适合稠密图。

#### 3.1.2 广度优先搜索在图论中的实现

广度优先搜索（BFS）算法是一种图论算法，用于遍历图中的所有顶点。BFS算法从一个起始顶点开始，首先访问该顶点的所有相邻顶点，然后访问这些相邻顶点的相邻顶点，以此类推，直到遍历完所有顶点。

BFS算法的实现步骤如下：

1. 初始化一个队列，将起始顶点入队。
2. 循环执行以下步骤，直到队列为空：
- 出队队首元素，并访问该顶点。
- 将该顶点的所有未访问的相邻顶点入队。

### 3.2 广度优先搜索算法的应用场景

BFS算法在图论中有着广泛的应用，主要应用场景包括：

#### 3.2.1 连通性判断

BFS算法可以用来判断图是否连通。如果图中存在一条从起始顶点到所有其他顶点的路径，则图是连通的；否则，图是不连通的。

#### 3.2.2 最短路径查找

BFS算法可以用来查找图中从起始顶点到其他顶点的最短路径。最短路径是指边数最少的路径。

**代码示例：**

# 使用邻接表表示图
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# BFS算法
def bfs(graph, start):
    queue = [start]
    visited = set()
    while queue:
        vertex = queue.pop(0)
        if vertex not in visited:
            visited.add(vertex)
            for neighbor in graph[vertex]:
                if neighbor not in visited:
                    queue.append(neighbor)

# 判断图是否连通
def is_connected(graph):
    bfs(graph, list(graph.keys())[0])
    return len(visited) == len(graph)

# 查找最短路径
def shortest_path(graph, start, end):
    queue = [(start, 0)]
    visited = set()
    while queue:
        vertex, distance = queue.pop(0)
        if vertex not in visited:
            visited.add(vertex)
            if vertex == end:
                return distance
            for neighbor in graph[vertex]:
                if neighbor not in visited:
                    queue.append((neighbor, distance + 1))
    return -1  # 未找到路径

# 4