【Java中的回溯算法与搜索策略】：深度优先搜索与广度优先搜索的对比分析

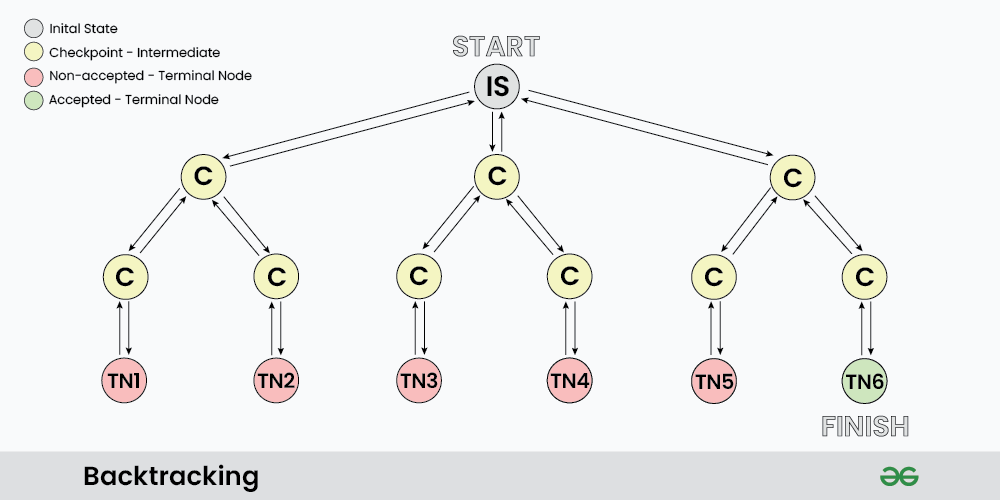
# 1. 回溯算法与搜索策略概述

在现代信息技术领域中，算法设计是构建复杂系统的基础。回溯算法作为一种重要的搜索策略，在解决各种优化问题中扮演着关键角色。它能够系统地探索所有可能的候选解，以找到问题的最优解或任意解。本章将对回溯算法进行简要概述，介绍其基本概念和搜索策略，为深入理解后续章节奠定基础。

## 1.1 回溯算法的基本概念

回溯算法是一种通过试错来寻找问题解的算法。它在执行过程中，每当遇到不满足条件的情况时，就会取消上一步或几步的操作，再通过其他路径继续尝试寻找解决方案，从而避免陷入无解的无限循环。

## 1.2 搜索策略的重要性

搜索策略决定了在特定问题空间中寻找解的效率和有效性。它不仅包括了算法的逻辑结构，还涉及到数据结构的使用、回溯的时机和剪枝的策略等。正确的搜索策略能够显著减少搜索空间，提高算法的运行效率。

## 1.3 本章小结

回溯算法和搜索策略是解决大量计算机科学问题的关键工具。本章首先介绍了回溯算法的基本概念，为读者提供了初步的认识，然后强调了搜索策略的重要性，为后续章节中具体的实现与应用铺垫了理论基础。

# 2. 回溯算法的理论基础

### 2.1 回溯算法概念解析

#### 2.1.1 回溯算法的定义与特点

回溯算法是一种通过试错来寻找所有解的算法，它在必要时回退并放弃前一次尝试的解决方案，逐渐向正确的方向推进。这种策略适用于求解约束满足问题，如八皇后问题、图的着色、子集求和等问题。

回溯算法的特点可以概括为：
- **试错性质**：算法尝试所有可能的解，一旦发现当前选择不可能得到有效的解决方案，就回退到上一步进行尝试。
- **递归实现**：回溯算法通常用递归的方式实现，通过调用自身来探索所有可能的选择路径。
- **剪枝优化**：为了提高搜索效率，可以使用剪枝技术提前终止不可能产生解的路径。
- **全局搜索**：它并不追求局部最优，而是尝试找到全局最优解。

#### 2.1.2 回溯算法的典型应用领域

回溯算法在许多领域都有广泛应用，特别是那些需要穷举所有可能性来找到正确答案的场景：
- **人工智能**：在游戏树搜索、专家系统和规划问题中，回溯算法用来求解问题的最优解。
- **组合优化**：解决各种组合问题，如排列组合、图论问题等。
- **数据挖掘**：在数据挖掘中，回溯算法用于特征选择、模型选择等。
- **编程竞赛**：在国际编程竞赛中，许多问题都可以用回溯算法解决。

### 2.2 搜索策略的基本分类

#### 2.2.1 搜索问题的基本要素

搜索问题的基本要素包括状态、状态空间、起始状态、目标状态、路径和搜索树。

- **状态**：问题在某一特定时刻的具体表现形式。
- **状态空间**：所有可能状态的集合。
- **起始状态**：问题解决的起始点。
- **目标状态**：问题解决的终点。
- **路径**：从起始状态到目标状态的转换序列。
- **搜索树**：以状态为节点、转换为边的树形结构，用于表示搜索过程。

#### 2.2.2 搜索策略的比较标准

在选择搜索策略时，通常考虑以下标准：
- **时间复杂度**：解决问题所需的时间。
- **空间复杂度**：算法运行过程中占用的存储空间。
- **完备性**：算法是否总是能找到问题的解（如果存在的话）。
- **最优性**：算法找到的是否总是最优解。
- **局部搜索能力**：算法对于局部问题的处理能力。

接下来我们将详细介绍深度优先搜索和广度优先搜索的实现方法与应用。

# 3. 深度优先搜索的实现与应用

## 3.1 深度优先搜索的算法原理

### 3.1.1 搜索树的构建过程

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。其核心思想是尽可能深地搜索树的分支，当节点v的所在边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。

如果我们要在搜索树中构建节点，我们可以用以下步骤：

1. 创建一个空栈，压入起始节点。
2. 当栈不为空时，重复以下过程：
a. 弹出栈顶元素，并对其进行处理。
b. 将所有与该节点相关联的未被访问过的节点压入栈中。
c. 重复步骤b，直到所有相关节点都被访问。

这个过程实际上是在模拟递归的调用过程。在DFS的回溯过程中，一个被压入栈的节点会在它的所有子节点都被访问过后才被处理，这保证了我们尽可能地沿着一条路径深入。

### 3.1.2 深度优先搜索的递归实现

深度优先搜索的递归实现本质上是对算法原理的直接映射。递归形式的DFS非常适合于树结构，因为树的特性自然符合DFS的递归调用逻辑。

def DFS(graph, node, visited):
    if node not in visited:
        print(node, end=' ')  # 处理节点
        visited.add(node)
        for neighbour in graph[node]:
            DFS(graph, neighbour, visited)

在上述代码中：

- `graph` 是一个字典，其中键是节点，值是与该节点相连的其他节点的