【Java回溯算法与动态规划】：深度比较与综合运用策略

# 1. Java回溯算法与动态规划概述

在算法设计的广阔领域中，回溯算法和动态规划是解决复杂数学与优化问题的两大利器。本章将作为系列文章的总览，简要介绍这两种算法的基本概念、应用场景及它们之间的联系与差异。

## 1.1 算法的核心价值

回溯算法和动态规划都致力于通过递归或迭代的方式解决组合优化问题。回溯算法通过探索所有可能的候选解来找出所有解，而动态规划则在候选解的重叠子问题中保存结果，避免了重复计算。

## 1.2 Java语言中的实践意义

Java作为一种成熟的编程语言，其简洁的语法和强大的库支持，使开发者可以更轻松地实现这两种算法，并运用于实际问题中。掌握它们在Java中的实现方法，对于提升解决复杂问题的效率至关重要。

## 1.3 本系列文章的路线图

接下来的章节将深入探讨回溯算法和动态规划的理论基础和实现细节，以及它们在实际问题中的应用。我们会以代码实例和案例分析为主，引导读者逐步掌握这两种算法的精髓。

通过本章，读者应建立起对回溯算法和动态规划的初步理解，为深入学习后续章节内容奠定基础。

# 2. ```
# 第二章：理解回溯算法

## 2.1 回溯算法理论基础
### 2.1.1 回溯算法定义
回溯算法是一种通过探索所有可能的候选解来找出所有解的算法，如果候选解被确认不是一个解，则回溯返回，尝试其他路径。它是一种走不通就回退的搜索策略。其特点是使用递归来实现，在每一个可能的解空间上进行尝试，如果发现当前尝试不可能得出解，则撤销上一步甚至上几步的计算，再通过其他的可能的解进行尝试。

在更具体的编程实践上，回溯算法通常和状态空间树紧密相关。在状态空间树中，每一个节点表示问题求解的一个状态，子节点代表由当前状态通过一定操作得到的新状态，而回溯算法的工作就是在整个状态空间树上进行遍历，寻找一个或所有满足条件的解。

### 2.1.2 回溯算法的典型应用场景
回溯算法的典型应用场景包括但不限于：

- 组合问题：如集合的全排列、组合总和等。
- 选择问题：例如八皇后问题、图的着色、装箱问题等。
- 搜索问题：比如迷宫问题、汉密尔顿回路、NP完全问题等。

由于其逐个尝试的特性，回溯算法特别适合解决需要穷举所有可能情况的优化问题。

## 2.2 回溯算法的关键步骤
### 2.2.1 状态空间树的构建
状态空间树是回溯算法搜索过程的抽象表示，它通过树形结构展示所有可能的搜索路径。构建状态空间树首先需要定义问题的解空间，然后根据问题的约束条件，从根节点出发不断进行分支，形成树的各个节点。每一个节点代表当前状态下的一个决策，通过递归调用或者迭代方法逐步向更深的层级搜索。

每个节点的子节点对应从当前状态出发的可能的新状态。通常，回溯算法需要考虑状态空间树的深度优先遍历，因为这样可以减少内存的占用，更适合解决大规模的问题。

### 2.2.2 剪枝技术与优化策略
剪枝技术是回溯算法中提高效率的关键，它是在状态空间树的构建过程中，动态地去掉一些不可能产生解的节点，从而避免无谓的搜索。剪枝的判断依据通常依赖于问题的特定约束条件。

优化策略是指在实施回溯算法时，考虑如何高效地构建和遍历状态空间树，这可能包括：
- 按某种顺序访问孩子节点，以达到剪枝效果。
- 记录已经搜索过的节点信息，避免重复搜索。
- 使用双向搜索或启发式搜索等技术减少搜索空间。

## 2.3 回溯算法的代码实现
### 2.3.1 递归框架的构建
在实现回溯算法时，递归是一种常用的编程技巧，因为它自然地模拟了状态空间树的生成和搜索过程。递归框架通常包括两个主要部分：递归函数和终止条件。

// 递归函数
public void backtrack(参数列表) {
    if (终止条件) {
        // 处理结果或输出结果
        return;
    }
    // 遍历所有可能的下一步决策
    for (可能的决策 : 决策列表) {
        // 执行决策，并更新状态
        makeDecision(可能的决策);
        // 递归调用
        backtrack(新的参数列表);
        // 回溯，撤销决策
        undoDecision(可能的决策);
    }
}

// 调用回溯函数的主函数
public void solveProblem() {
    // 初始化状态
    backtrack(初始参数);
}

在上述代码模板中，`backtrack`是核心的递归函数，每次递归时首先检查是否满足终止条件，如果不满足则遍历所有可能的决策，进行决策并递归，最后回溯。

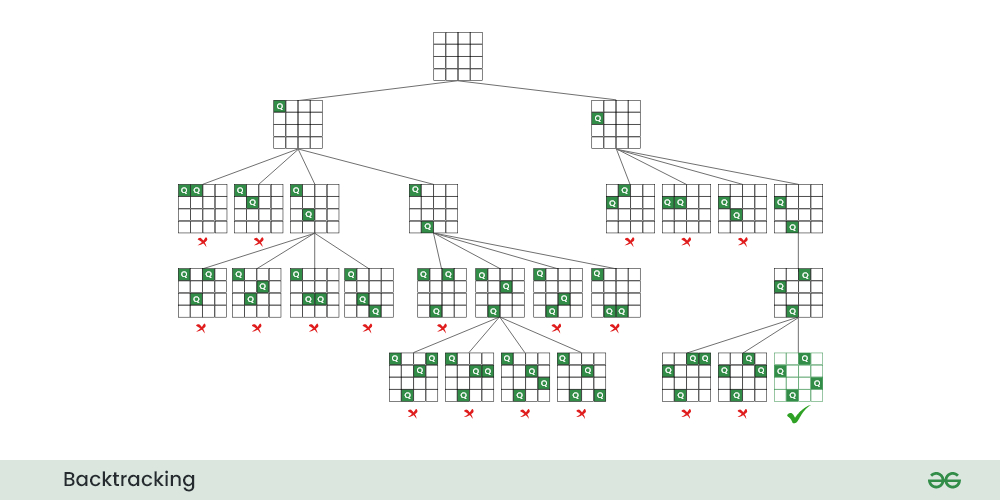
### 2.3.2 实例分析：八皇后问题
八皇后问题是一个经典的回溯算法应用问题，要求在8×8的棋盘上放置8个皇后，使得它们互不攻击。即任何两个皇后都不在同一行、同一列或同一对角线上。

// 棋盘大小
int size = 8;
// 存储皇后的列位置
int[] columns = new int[size];
// 初始化棋盘
public void solveNQueens() {
    backtrack(0);
}

private void backtrack(int row) {
    // 终止条件，所有皇后都放置好了
    if (row == size) {
        printSolution();
        return;
    }
    // 尝试在当前行放置皇后，并检查是否有冲突
    for (int col = 0; col < size; col++) {
        if (isSafe(row, col)) {
            columns[row] = col;
            backtrack(row + 1);
        }
    }
}

// 检查放置皇后的位置是否安全
private boolean isSafe(int row, int col) {
    for (int i = 0; i < row; i++) {
        if (columns[i] == col || 
            i - columns[i] == row - col || 
            i + columns[i] == row + col) {
            return false;
        }
    }
    return true;
}

// 输出解决方案
private void printSolution() {
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            if (columns[i] == j) {
                System.out.print("Q ");
            } else {
                System.out.print(". ");
            }
        }
        System.out.println();
    }
    System.out.println();
}

在上面的代码中，`columns`数组记录每一行皇后的列位置，`isSafe`函数用于检查皇后是否处于安全的位置。通过递归地调用`backtrack`函数，我们可以找到所有可能的解决方案。

通过实例分析，我们可以看到回溯算法的核心就是深度优先搜索加回溯策略，在搜索过程中不断尝试并排除不可能的路径，最终找到问题的解答。

# 3. 探索动态规划

动态规划作为解决复杂问题的一种策略，经常与回溯算法相提并论。它不仅在理论上有着严谨的构建，在实际应用中也有着广泛的运用。在第三章中，我们将深入探索动态规划，理解其理论基础，掌握实现方法，并了解在实际问题中的应用。

## 动态规划理论解析

动态规划是一种将复杂问题分解为更小的子问题，并存储子问题解以避免重复计算的方法。它利用了问题的最优子结构和重叠子问题的性质，通过构建状态和状态转移方程来求解原问题。

### 动态规划的基本概念

动态规划的基本思想是将原问题分解为相对简单的子问题，先求解子问题，再利用子问题的解求解原问题。其关键在于识别子问题、构建状态，并找出状态之间的关系，即状态转移方程。

在动态规划中，状态通常表示为`dp[i][j]`，其中`i`和`j`分别代表问题的某个维度。状态的定义需要能够代表问题的当前状态，而状态转移方程则是根据问题的条件来定义如何从一个或多个较小的状态得到当前状态。

### 动态规划的数学模型

动态规划的数学模型通常由以下几个部分组成：

- 状态定义：确定状态，也就是定义`dp[i][j]`的意义。
- 状态转移方程：找到不同状态之间的关系。
- 初始条件：确定动态规划的起点，即`dp[0][0]`等基础状态。
- 答案：根据状态定义和状态转移方程来确定最终的答案。

动态规划问题可以是求最大值、最小值，也可以是求可行解的数量。对于不同的问题，状态的定义和转移方程需要单独设计和推导。

## 动态规划的实现方法

在实现动态规划时，我们遵循一些固定的模式和步骤。这些步骤有助于我们系统地解决动态规划问题。

### 状态定义与转移方程

状态定义是动态规划中的核心。我们需要定义一个或多个状态来表示问题的不同阶段或子问题的解。状态定义必须足够清晰，能够覆盖整个问题空间，且易于通过状态转移方程进行计算。

以背包问题为例，状态`dp[i][w]`可以定义为：对于前`i`个物品，在不超过背包容量`w`的条件下能够获得的最大价值。状态转移方程则描述了如何从子问题的状态来获得当前状态的值：

dp[i][w] = max(dp[i-1][w], dp[i-1][w - wt[i]] + val[i])

### 动态规划与递归的对比

动态规划通常可以看作是带有记忆化的递归。记忆化是指在递归过程中，将已经计算过的子问题的解存储起来，当下次遇到相