回溯算法优化策略：Java中减少计算量的实用技巧

# 1. 回溯算法概述及应用实例

## 1.1 回溯算法的定义和重要性
回溯算法是一种通过试错来寻找所有解的算法，它是一种递归式的算法，通常用于解决约束满足问题。在解决问题的过程中，一旦发现已不满足求解条件，即“回溯”返回，尝试其他路径。

## 1.2 回溯算法的典型应用场景
回溯算法广泛应用于组合问题、排列问题、图的路径寻找问题等领域。例如，经典的N皇后问题、旅行商问题、图的着色问题等。

## 1.3 一个应用实例：N皇后问题
N皇后问题要求在N×N的棋盘上放置N个皇后，使得它们互不攻击。这正是回溯算法能够发挥作用的场景之一。我们将通过详细的步骤展示如何使用回溯算法解决N皇后问题。

# 2. 理解回溯算法的计算过程

## 2.1 回溯算法的基本原理

### 2.1.1 回溯算法的定义和特性

回溯算法是一种通过递归方式来遍历所有可能性，并在发现当前分枝不可能得到正确结果时，就“回溯”返回，尝试其他分枝的算法。它的特性体现在以下几个方面：

- 全局搜索：尝试所有可能的候选解来找到问题的所有解。
- 剪枝操作：在搜索过程中，放弃不必要继续探索的分枝。
- 约束满足：通常需要结合问题的特定约束来避免无效探索。

回溯算法常用于解决约束满足问题，如数独、图的着色、旅行商问题等。

### 2.1.2 回溯算法的典型应用场景

- 组合问题：比如全排列、组合求和问题。
- 选择问题：如八皇后、0-1背包问题。
- 子集问题：比如集合的幂集、组合问题等。
- 图论问题：如旅行商问题、图的着色问题。

## 2.2 回溯算法的实现框架

### 2.2.1 核心算法结构解析

回溯算法的核心是一个递归函数，通常包含以下步骤：

1. **确定递归的基本条件**，决定何时返回。
2. **进行选择**，决定哪个变量、哪个值。
3. **做出选择**，更新当前状态。
4. **探索所有可能性**，递归调用。
5. **撤销选择**，回到上一个状态。

伪代码如下：

function backtrack(path, options):
    if meet the base condition:
        process the path
        return
    for each option in options:
        if option is valid:
            add option to path
            backtrack(path, remaining_options)
            remove option from path

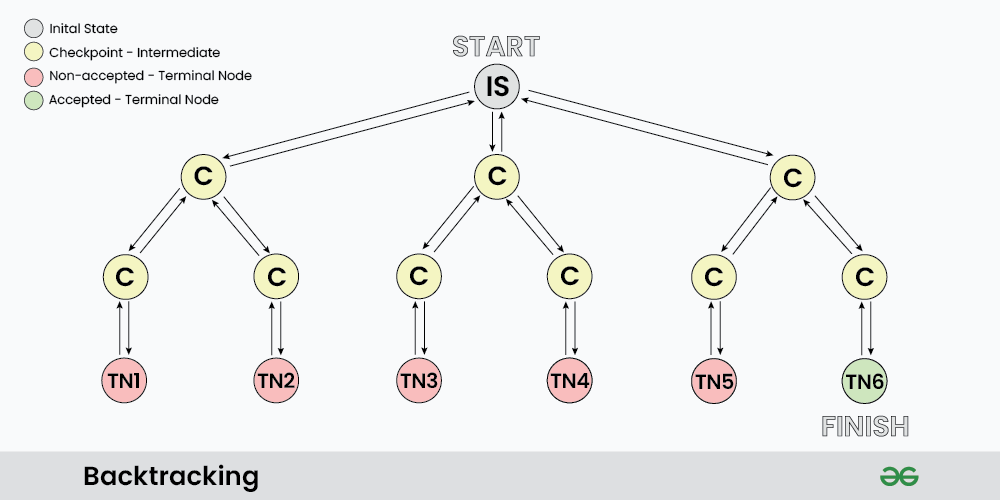
### 2.2.2 状态空间树的概念和构建

回溯算法的状态空间树是一种树形结构，树中的每个节点代表一个解空间的状态，节点的子节点代表由当前状态进行选择得到的下一个状态。

- **根节点**：代表问题的起始状态。
- **叶节点**：代表问题的一个可能解。
- **分支节点**：代表需要做决策的状态点。

构建状态空间树是回溯算法的核心部分，可以使用递归函数自然地构建出这棵树。

### 2.2.3 剪枝技术的引入和必要性

剪枝是回溯算法中用于优化性能的手段，主要目的是减少搜索空间，避免不必要的计算。

- **必要性**：在复杂问题中，如果不进行剪枝，可能会产生大量的无效解，导致算法效率极低。
- **剪枝技术**：包括基于问题约束的剪枝、基于已探索路径的剪枝等。

## 2.3 回溯算法的性能影响因素

### 2.3.1 计算复杂度分析

回溯算法的复杂度分析通常关注于递归深度和分支因子：

- **递归深度**：决定了算法要处理多少层状态空间树。
- **分支因子**：每个节点有多少个子节点。

这两个因素直接决定了算法的执行时间和空间消耗。

### 2.3.2 影响回溯性能的关键因素

影响回溯算法性能的关键因素包括：

- **问题规模**：问题规模越大，可能的状态空间也越大。
- **剪枝效率**：剪枝策略越有效，能减少更多的无效搜索。
- **最优解的位置**：最优解越早出现在状态空间树中，算法越早找到解，效率越高。

通过选择合适的策略和数据结构，可以在实际应用中大幅提升回溯算法的性能。

# 3. 优化回溯算法的实用技巧

## 3.1 排列组合优化

回溯算法在求解排列组合问题时，经常会出现重复的解，这会无谓地增加算法的计算量。因此，优化的首要目标就是去除这些重复解，以提高算法效率。

### 3.1.1 去除重复解的方法

在解决排列组合问题时，通常可以采用集合（Set）来存储已经生成的解。当一个解被完整构造后，我们将其加入到集合中。如果在后续过程中再次生成了相同的解，由于集合不允许重复元素，算法会自动忽略它。

下面是一个简单的示例，演示如何在回溯算法中使用集合去除重复解：

public Set<List<Integer>> res = new HashSet<>();
public List<List<Integer>> permute(int[] nums) {
    List<Integer> output = new ArrayList<>();
    backTrack(nums, output);
    return new ArrayList<>(res);
}

private void backTrack(int[] nums, List<Integer> output) {
    if (output.size() == nums.length) {
        res.add(new ArrayList<>(output));
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        output.add(nums[i]);
        backTrack(nums, output);
        output.remove(output.size() - 1);
    }
}

这段代码是一个生成排列的回溯算法。在`backTrack`函数中，每次递归调用都会尝试向`output`列表中添加一个新的数字。当`output`列表达到与`nums`数组相同的长度时，说明一个解已被完整构造。此时，通过将`output`转换为一个`ArrayList`并添加到结果集合`res`中，可以确保不会有重复的解。

### 3.1.2 优化递归深度的策略

在排列问题中，可以通过优化递归深度来减少不必要的计算。一种常见的策略是在每层递归中仅考虑尚未使用过的元素。

private void backTrack(int[] nums, List<Integer> output, boolean[] used) {
    if (output.size() == nums.length) {
        res.add(new ArrayList<>(output));
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        if (used[i]) {
            continue;
        }
        used[i] = true;
        output.add(nums[i]);
        backTrack(nums, output, used);
        output.remove(output.size() - 1);
        used[i] = false;
    }
}

这里引入了一个`used`数组来记录哪些元素已经被添加到了当前解中。在每次递归调用中，我们只遍历那些`used`数组标记为`false`的元素，这可以显著减少递归调用的次数，因为跳过了那些已经考虑过的元素。

## 3.2 基于问题特性的优化

针对特定问题，可以利用问题的特性来进一步优化回溯算法的性能。例如，对于N皇后问题，由于问题对称性，可以在搜索树中剪掉大量的对称分支，从而降低解空间的大小。

### 3.2.1 问题约束的分析和应用

在N皇后问题中，每行每列只能放置一个皇后，这为剪枝提供了依据。我们可以在生成新的解时，根据已经放置的皇后的情况，避免在它们的攻击范围内放置新的皇后。

private void placeQueen(int row, int[] cols, boolean[] diag1, boolean[] diag2) {
    if (row == cols.length) {
        // 检查是否可以放置皇后
        for (int i = 0; i < cols.length; i++) {
            if (cols[i] == row || diag1[row + i] || diag2[row - i + cols.length - 1]) {
                return; // 不能放置，回溯
            }
        }
        // 放置成功，继续向下一行
        placeQueen(row + 1, cols, diag1, diag2);
        return;
    }
    // 尝试在当前行的不同列中放置皇后
    for (int col = 0; col < cols.length; col++) {