图论算法实战：掌握深度优先搜索和广度优先搜索的秘诀

# 1. 图论基础**

图论是计算机科学中研究图结构及其算法的一门学科。图由一系列节点和连接这些节点的边组成。图论算法用于解决各种问题，例如连通性检测、最短路径查找和拓扑排序。

图论中的基本概念包括：

* **节点：**图中的基本元素，表示实体或对象。
* **边：**连接两个节点的线段，表示节点之间的关系或交互。
* **权重：**与边关联的值，表示边上的成本或距离。
* **路径：**节点的有序序列，其中每两个相邻节点都由一条边连接。
* **连通图：**所有节点都直接或间接连接的图。

# 2. 深度优先搜索**

**2.1 DFS的基本原理**

深度优先搜索（DFS）是一种图论算法，它通过递归或栈的方式沿着一条路径深度探索图中的节点。DFS从一个起始节点开始，访问该节点的所有未访问的相邻节点，然后递归地访问这些相邻节点的未访问的相邻节点，依此类推。

**2.2 DFS的实现与应用**

**2.2.1 递归实现**

def dfs_recursive(graph, start_node):
    """
    深度优先搜索的递归实现

    参数：
        graph: 图的邻接表表示
        start_node: 起始节点
    """
    visited = set()  # 存储已访问的节点

    def dfs_helper(node):
        if node in visited:
            return

        visited.add(node)
        print(node)  # 访问节点

        for neighbor in graph[node]:
            dfs_helper(neighbor)

    dfs_helper(start_node)

**代码逻辑分析：**

* `dfs_recursive`函数接收图的邻接表表示和起始节点作为参数。
* 初始化一个集合`visited`来存储已访问的节点。
* 定义辅助函数`dfs_helper`，它递归地访问节点及其未访问的相邻节点。
* 如果节点已访问，则返回。
* 将节点标记为已访问并打印它。
* 遍历节点的所有相邻节点，并递归地调用`dfs_helper`访问它们。

**2.2.2 栈实现**

def dfs_stack(graph, start_node):
    """
    深度优先搜索的栈实现

    参数：
        graph: 图的邻接表表示
        start_node: 起始节点
    """
    stack = [start_node]  # 初始化栈
    visited = set()  # 存储已访问的节点

    while stack:
        node = stack.pop()  # 弹出栈顶元素
        if node in visited:
            continue

        visited.add(node)
        print(node)  # 访问节点

        for neighbor in graph[node]:
            if neighbor not in visited:
                stack.append(neighbor)

**代码逻辑分析：**

* `dfs_stack`函数接收图的邻接表表示和起始节点作为参数。
* 初始化一个栈`stack`和一个集合`visited`来存储已访问的节点。
* 循环遍历栈，直到栈为空。
* 弹出栈顶元素`node`，并检查它是否已访问。如果已访问，则跳过。
* 将`node`标记为已访问并打印它。
* 遍历`node`的所有未访问的相邻节点，并将其推入栈中。

**2.3 DFS的优化技巧**

为了提高DFS的效率，可以使用以下优化技巧：

* **颜色标记：**使用颜色标记来跟踪节点的状态（白色：未访问，灰色：正在访问，黑色：已访问）。
* **路径压缩：**在递归实现中，对每个节点只访问一次，避免重复访问。
* **循环检测：**在递归实现中，使用栈或队列来检测循环，避免无限递归。

# 3.1 BFS的基本原理

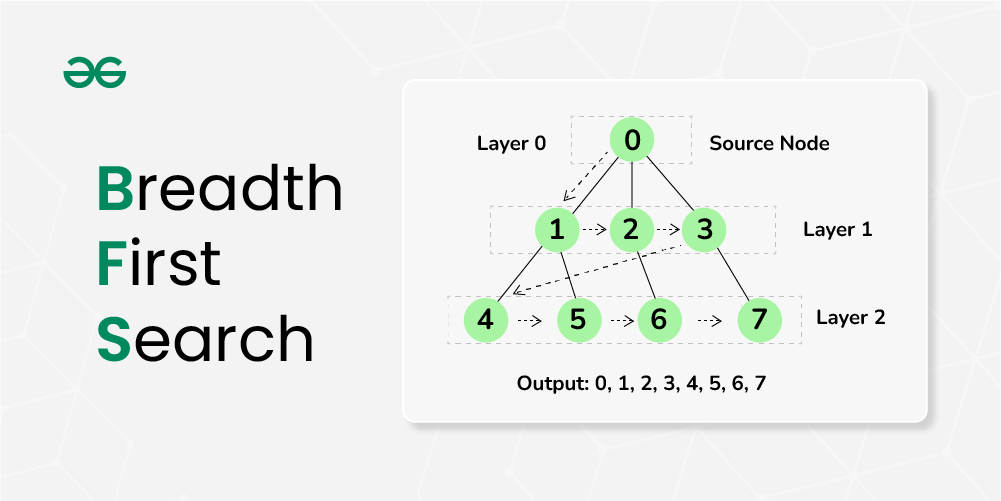
广度优先搜索（BFS）是一种图论算法，它按照图的层次来遍历图中的节点。与深度优先搜索（DFS）不同，BFS不会深入探索一条路径，而是先访问所有与当前节点相邻的节点，然后再访问与这些节点相邻的节点，以此类推。

BFS的基本原理是使用队列数据结构。队列是一种先进先出（FIFO）的数据结构，它可以用来存储要访问的节点。算法从图中的一个起始节点开始，将该节点加入队列。然后，算法从队列中取出第一个节点，并访问其所有相邻节点。这些相邻节点被添加到队列中，然后算法继续从队列中取出节点并访问其相邻节点，直到队列为空。

### 3.2 BFS的实现与应用

#### 3.2.1 队列实现

BFS算法可以使用队列数据结构来实现。以下是用Python实现的BFS算法：

def bfs(graph, start):
    queue = [start]
    visited = set()

    while queue:
        node = queue.pop(0)  # 从队列中取出第一个节点
        if node not in visited:
            visited.add(node)  # 将节点标记为已访问
            for neighbor in graph[node]:  # 遍历节点的所有相邻节点
                if neighbor not in visited:
                    queue.append(neighbor)  # 将相邻节点添加到队列中

**代码逻辑分析：**

1. 该函数接受两个参数：`graph`（图的邻接表表示）和`start`（起始节点）。
2. 它使用一个队列`queue`来存储要访问的节点，并使用一个集合`visited`来跟踪已访问的节点。
3. 算法从队列中取出第一个节点`node`，并将其标记为已访问。
4. 然后，它遍历`node`的所有相邻节点，并将其添加到队列中，如果它们尚未被访问过。
5. 算法重复这个过程，直到队列为空，这意味着图中所有可达的节点都已被访问。

#### 3.2.2 层次遍历

BFS算法的一个常见应用是层次遍历，它以层次结构的形式打印图中的节点。层次遍历从起始节点开始，并逐层打印图中的节点。

以下是用Python实现的层次遍历算法：

def bfs_level_order(graph, start):
    queue = [start]
    level = 0
    while queue:
        size = len(queue)  # 当前层的节点数
        print(f"Level {level}: ", end="")
        for i in range(size):
            node = queue.pop(0)  # 从队列中取出第一个节点
            print(node, end=" ")
            for neighbor in graph[node]:  # 遍历节点的所有相邻节点
                if neighbor not in queue:
                    queue.append(neighbor)  # 将相邻节点添加到队列中
        level += 1  # 进入下一层

**代码逻辑分析：**

1. 该函数接受两个参数：`graph`（图的邻接表表示）和`start`（起始节点）。
2. 它使用一个队列`queue`来存储要访问的节点，并使用一个变量`level`来跟踪当前的层次。
3. 算法从队列中取出当前层的节点，并打印它们。
4. 然后，它遍历每个节点的所有相邻节点，并将其添加到队列中，如果它们尚未被访问过。
5. 算法重复这个过程，直到队列为空，这意味着图中所有可达的节点都已被访问。

# 4. 图论算法实战**

**4.1 连通分量检测**

连通分量检测是图论中的一项基本算法，用于识别图中相互连接的顶点集合。连通分量检测的应用广泛，例如：

- 社交网络分析：识别社交网络中紧密联系的群组。
- 交通网络优化：确定道路网络中相互连接的区域。
- 推荐系统：根据用户行为识别相似用户组。

**4.1.1 深度优先搜索法**

深度优先搜索法（DFS）是一种递归算法，用于检测连通分量。DFS算法从一个顶点开始，深度遍历图，直到访问所有可达的顶点。DFS算法的伪代码如下：

def dfs(graph, vertex):
    visited.add(vertex)
    for neighbor in graph[vertex]:
        if neighbor not in visited:
            dfs(graph, neighbor)

**参数说明：**

- `graph`：图的邻接表表示。
- `vertex`：当前访问的顶点。

**代码逻辑：**

DFS算法首先将当前顶点标记为已访问，然后遍历当前顶点的所有邻接顶点。如果邻接顶点未被访问，则递归调用DFS算法继续遍历。

**4.1.2 广度优先搜索法**

广度优先搜索法（BFS）是一种基于队列的算法，用于检测连通分量。BFS算法从一个顶点开始，逐层遍历图，直到访问所有可达的顶点。BFS算法的伪代码如下：

def bfs(graph, vertex):
    queue.append(vertex)
    while queue:
        current_vertex = queue.pop(0)
        visited.add(current_vertex)
        for neighbor in graph[current_vertex]:
            if neighbor not in visited:
                queue.append(neighbor)

**参数说明：**

- `graph`：图的邻接表表示。
- `vertex`：当前访问的顶点。

**代码逻辑：**

BFS算法首先将当前顶点加入队列，然后逐层遍历图。每次从队列中取出一个顶点，并将其标记为已访问。然后遍历当前顶点的所有邻接顶点，如果邻接顶点未被访问，则将其加入队列。

**4.2 最短路径算法**

最短路径算法用于计算图中两点之间的最短路径。最短路径算法的应用广泛，例如：

- 导航系统：计算从起点到目的地的最短路线。
- 网络优化：优化网络流量的路由。
- 供应链管理：确定从供应商到客户的最短运输路径。

**4.2.1 Dijkstra算法**

Dijkstra算法是一种贪心算法，用于计算图中从一个顶点到所有其他顶点的最短路径。Dijkstra算法的伪代码如下：

def dijkstra(graph, source):
    dist[source] = 0
    while unvisited:
        current_vertex = min(unvisited, key=lambda vertex: dist[vertex])
        unvisited.remove(current_vertex)
        for neighbor in graph[current_vertex]:
            new_dist = dist[current_vertex] + graph[current_vertex][neighbor]
            if new_dist < dist[neighbor]:
                dist[neighbor] = new_dist
                prev[neighbor] = current_vertex

**参数说明：**

- `graph`：图的邻接表表示，其中边权重存储在`graph[u][v]`中。
- `source`：源顶点。

**代码逻辑：**

Dijkstra算法首先将源顶点的距离初始化为0，然后迭代遍历图中未访问的顶点。每次选择距离源顶点最小的未访问顶点，并将其标记为已访问。然后遍历当前顶点的所有邻接顶点，更新邻接顶点的距离和前驱顶点。

**4.2.2 Floyd算法**

Floyd算法是一种动态规划算法，用于计算图中所有点对之间的最短路径。Floyd算法的伪代码如下：

def floyd_warshall(graph):
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]

**参数说明：**

- `graph`：图的邻接矩阵表示，其中边权重存储在`graph[i][j]`中。

**代码逻辑：**

Floyd算法首先初始化距离矩阵`dist`，其中`dist[i][j]`表示从顶点`i`到顶点`j`的距离。然后算法迭代遍历所有顶点，并使用动态规划更新距离矩阵。对于每个顶点`k`，算法检查从顶点`i`到顶点`k`的距离加上从顶点`k`到顶点`j`的距离是否小于从顶点`i`到顶点`j`的当前距离。如果更小，则更新`dist[i][j]`。

**4.3 拓扑排序**

拓扑排序是一种算法，用于对有向无环图（DAG）中的顶点进行排序，使得对于任何一条从顶点`u`到顶点`v`的边，`u`在排序中都排在`v`之前。拓扑排序的应用广泛，例如：

- 任务调度：确定任务执行的顺序，以避免循环依赖。
- 软件构建：确定模块编译和链接的顺序。
- 数据流分析：确定数据流的顺序，以优化处理。

**4.3.1 Kahn算法**

Kahn算法是一种基于拓扑排序的算法，用于检测有向无环图（DAG）。Kahn算法的伪代码如下：

def kahn(graph):
    in_degree = [0] * n
    for vertex in graph:
        for neighbor in graph[vertex]:
            in_degree[neighbor] += 1
    queue = [vertex for vertex in graph if in_degree[vertex] == 0]
    while queue:
        current_vertex = queue.pop(0)
        for neighbor in graph[current_vertex]:
            in_degree[neighbor] -= 1
            if in_degree[neighbor] == 0:
                queue.append(neighbor)

**参数说明：**

- `graph`：有向无环图的邻接表表示。

**代码逻辑：**

Kahn算法首先初始化每个顶点的入度为0。然后算法遍历图，并为每个顶点计算其入度。入度为0的顶点被加入队列。算法从队列中取出顶点，并遍历其所有邻接顶点。对于每个邻接顶点，算法将入度减1。如果邻接顶点的入度变为0，则将其加入队列。算法重复执行此过程，直到队列为空。

# 5. 图论算法的应用

图论算法在现实世界中有着广泛的应用，从社交网络分析到交通网络优化，再到推荐系统。本章节将探讨图论算法在这些领域的实际应用。

### 5.1 社交网络分析

社交网络图是一个由节点（代表个人）和边（代表关系）组成的图。图论算法可以用来分析社交网络的结构和特性，从而揭示有关用户行为、信息传播和社区形成的见解。

#### 应用示例：社区检测

社区检测算法可以将社交网络划分为不同的社区，这些社区由紧密联系的节点组成。通过识别社区，我们可以了解用户的社交圈子、兴趣和影响力。

import networkx as nx

# 创建社交网络图
G = nx.Graph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E', 'F', 'G'])
G.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'D'), ('D', 'E'), ('E', 'F'), ('F', 'G')])

# 使用 Louvain 算法检测社区
communities = nx.community.greedy_modularity_communities(G)

# 打印社区
print("社区：")
for community in communities:
    print(community)

### 5.2 交通网络优化

交通网络图是一个由节点（代表路口）和边（代表道路）组成的图。图论算法可以用来优化交通流，减少拥堵和改善出行效率。

#### 应用示例：最短路径算法

最短路径算法可以找到从一个节点到另一个节点的最短路径。在交通网络中，我们可以使用最短路径算法来计算从起点到目的地的最佳路线。

import networkx as nx

# 创建交通网络图
G = nx.Graph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E'])
G.add_edges_from([('A', 'B', {'weight': 10}), ('A', 'C', {'weight': 15}), ('B', 'C', {'weight': 5}), ('B', 'D', {'weight': 12}), ('C', 'D', {'weight': 10}), ('D', 'E', {'weight': 8})])

# 使用 Dijkstra 算法计算从 A 到 E 的最短路径
path = nx.shortest_path(G, 'A', 'E', weight='weight')

# 打印最短路径
print("最短路径：")
print(path)

### 5.3 推荐系统

推荐系统旨在根据用户的历史行为和偏好为用户提供个性化的建议。图论算法可以用来构建用户-物品图，其中节点代表用户和物品，而边代表用户与物品之间的交互。

#### 应用示例：协同过滤

协同过滤算法通过分析用户-物品图中的相似性来推荐物品。相似性可以基于用户之间的共同评分或物品之间的共同用户。

import numpy as np
import pandas as pd

# 创建用户-物品评分矩阵
ratings = pd.DataFrame({
    'user': ['A', 'B', 'C', 'D', 'E'],
    'item': ['item1', 'item2', 'item3', 'item4', 'item5'],
    'rating': [5, 4, 3, 2, 1]
})

# 计算用户之间的相似性
user_similarity = ratings.corr(method='pearson')

# 使用余弦相似性推荐物品
def recommend_items(user, n):
    # 获取与给定用户最相似的 n 个用户
    similar_users = user_similarity.loc[user].sort_values(ascending=False).index[:n]

    # 获取这些用户评分最高的 n 个物品
    recommended_items = ratings[ratings['user'].isin(similar_users)]['item'].value_counts().index[:n]

    return recommended_items

# 推荐给用户 A 的物品
recommended_items = recommend_items('A', 3)

# 打印推荐的物品
print("推荐的物品：")
print(recommended_items)

# 6.1 加权图算法

在实际应用中，图的边通常带有权重，表示边之间的距离、成本或其他度量。加权图算法考虑了边的权重，以找到最优解。

### 加权图的表示

加权图可以使用邻接矩阵或邻接表来表示。邻接矩阵是一个二维数组，其中元素表示两个顶点之间的权重。邻接表是一个由顶点列表组成的数组，每个顶点都有一个指向其邻接边的链表。

### 加权图算法

加权图算法包括：

- **最短路径算法：**寻找从一个顶点到另一个顶点的最短路径。最常见的算法有：
- Dijkstra算法：用于在非负权重图中查找最短路径。
- Floyd算法：用于在任意权重图中查找最短路径。
- **最大生成树算法：**寻找图中连接所有顶点的权重和最小的子图。最常见的算法有：
- Kruskal算法：基于并查集实现。
- Prim算法：基于优先队列实现。
- **最小割算法：**寻找将图划分为两个子图的边集，使得子图之间的权重和最小。最常见的算法有：
- Ford-Fulkerson算法
- Edmonds-Karp算法

### 代码示例

以下代码演示了使用Dijkstra算法查找加权图中从顶点1到顶点5的最短路径：

import heapq

class Graph:
    def __init__(self, num_vertices):
        self.num_vertices = num_vertices
        self.edges = [[] for _ in range(num_vertices)]
        self.weights = [[] for _ in range(num_vertices)]

    def add_edge(self, u, v, weight):
        self.edges[u].append(v)
        self.weights[u].append(weight)

def dijkstra(graph, start):
    distance = [float('inf')] * graph.num_vertices
    distance[start] = 0
    pq = [(0, start)]

    while pq:
        current_distance, current_vertex = heapq.heappop(pq)

        if current_distance > distance[current_vertex]:
            continue

        for neighbor in graph.edges[current_vertex]:
            new_distance = current_distance + graph.weights[current_vertex][neighbor]
            if new_distance < distance[neighbor]:
                distance[neighbor] = new_distance
                heapq.heappush(pq, (new_distance, neighbor))

    return distance

# 创建一个加权图
graph = Graph(6)
graph.add_edge(0, 1, 4)
graph.add_edge(0, 2, 2)
graph.add_edge(1, 2, 3)
graph.add_edge(1, 3, 2)
graph.add_edge(2, 4, 6)
graph.add_edge(3, 4, 1)
graph.add_edge(4, 5, 5)

# 从顶点1查找最短路径
distances = dijkstra(graph, 1)
print(distances)