图论算法实战：揭秘深度优先搜索与广度优先搜索的应用

# 1. 图论基础**

图论是计算机科学中一个重要的分支，它用于表示和分析由节点和边组成的结构。图论在现实世界中有广泛的应用，例如社交网络、交通网络和计算机网络。

**图的基本概念**

* **节点：**图中的基本单元，通常表示实体或对象。
* **边：**连接两个节点的线段，表示节点之间的关系或交互。
* **权重：**边上可以附加一个值，表示边上的距离、容量或其他属性。
* **有向图：**边具有方向，表示从一个节点到另一个节点的单向关系。
* **无向图：**边没有方向，表示节点之间的双向关系。

# 2. 深度优先搜索

深度优先搜索（DFS）是一种图论算法，它通过递归的方式遍历图中的所有节点，深入探索每个分支，直到遍历完所有可能的路径。

### 2.1 DFS算法原理

DFS算法基于“后进先出”的原则，它从图中的一个起始节点开始，沿着一条路径一直向下探索，直到遇到死胡同（即没有未访问的邻接节点）。此时，算法会回溯到最近一个未完全探索的节点，继续沿着另一条路径探索。

### 2.2 DFS算法实现

以下是用Python实现的DFS算法：

def dfs(graph, start):
    """
    深度优先搜索算法

    参数：
        graph: 图的邻接表表示
        start: 起始节点
    """
    visited = set()  # 标记已访问的节点
    stack = [start]  # 栈，存储待访问的节点

    while stack:
        node = stack.pop()  # 弹出栈顶元素
        if node not in visited:
            visited.add(node)  # 标记已访问
            for neighbor in graph[node]:  # 遍历邻接节点
                if neighbor not in visited:
                    stack.append(neighbor)  # 压入栈中

### 2.3 DFS算法应用

DFS算法广泛应用于图论中，包括：

- **连通性检测：**判断图中是否存在从一个节点到另一个节点的路径。
- **环检测：**判断图中是否存在环。
- **拓扑排序：**对无环有向图进行排序，使得每个节点都排在所有指向它的节点之后。
- **迷宫求解：**寻找迷宫中的路径。

**代码示例：**

# 连通性检测

graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

print(dfs(graph, 'A'))  # 输出：['A', 'B', 'D', 'E', 'F', 'C']

**执行逻辑说明：**

1. 从节点'A'开始搜索，访问其邻接节点'B'和'C'。
2. 由于'B'未被访问，将其压入栈中。
3. 继续探索'B'的邻接节点'D'和'E'，并将其压入栈中。
4. 由于'D'和'E'均未被访问，继续探索其邻接节点。
5. 最终，访问完所有节点后，输出访问顺序。

**参数说明：**

- `graph`：图的邻接表表示，其中键为节点，值为该节点的邻接节点列表。
- `start`：DFS算法的起始节点。

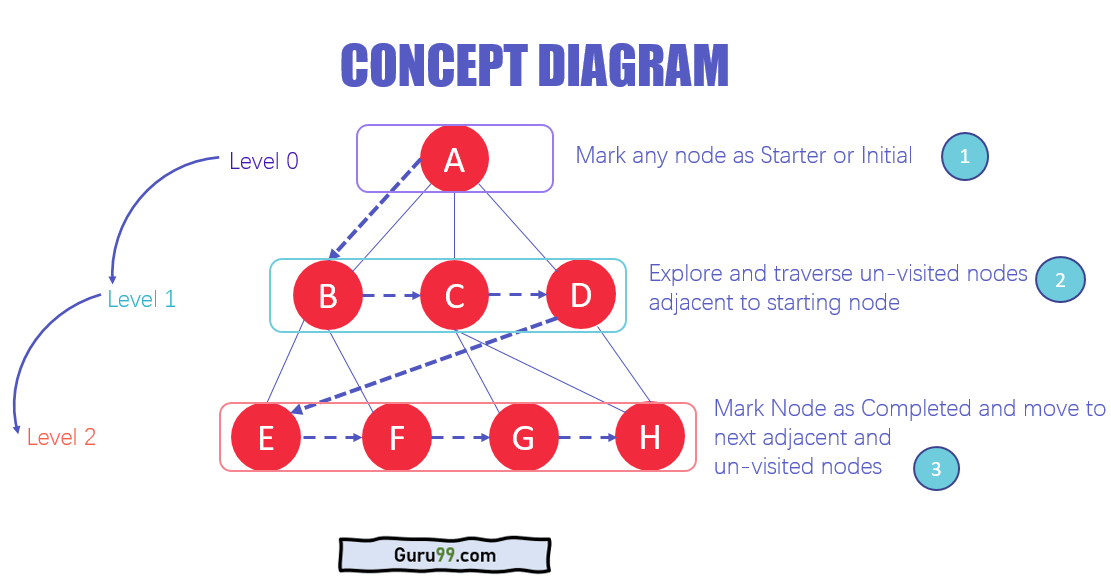
# 3.1 BFS算法原理

广度优先搜索（BFS）算法是一种图论算法，用于遍历