MATLAB求解方程组：稀疏矩阵求解，大规模方程组的克星

# 1. MATLAB求解方程组概述**

MATLAB是一种强大的技术计算语言，广泛用于求解方程组。方程组求解在科学、工程和金融等领域有着广泛的应用。MATLAB提供了一系列求解器和工具，可以高效地处理各种类型的方程组，包括线性方程组、非线性方程组和微分方程。

在本章中，我们将概述MATLAB求解方程组的原理、方法和应用。我们将讨论不同求解器的选择标准，并介绍MATLAB中可用的各种求解器。此外，我们将探讨求解方程组的常见挑战，例如稀疏矩阵和大型方程组，并介绍MATLAB中解决这些挑战的策略。

# 2. 稀疏矩阵理论与应用

### 2.1 稀疏矩阵的概念和特点

#### 2.1.1 稀疏矩阵的定义和表示

稀疏矩阵是一种特殊的矩阵，其中大部分元素为零。与稠密矩阵相比，稀疏矩阵具有以下特点：

- **非零元素稀少：**稀疏矩阵中非零元素的数量远少于零元素。
- **结构化：**稀疏矩阵中的非零元素通常分布在特定的模式中，形成特定的结构。

#### 2.1.2 稀疏矩阵的存储格式

为了高效地存储稀疏矩阵，需要使用专门的存储格式。常见的稀疏矩阵存储格式包括：

- **坐标格式 (COO)：**以非零元素的坐标 (行号、列号) 和值存储。
- **压缩行存储格式 (CSR)：**以行指针和列索引数组存储。
- **压缩列存储格式 (CSC)：**以列指针和行索引数组存储。

### 2.2 稀疏矩阵求解方法

稀疏矩阵的求解方法主要分为两类：

#### 2.2.1 直接求解法

直接求解法通过一次性计算获得精确解，常见的直接求解法有：

- **高斯消元法：**使用行变换将矩阵化为上三角形，再回代求解。
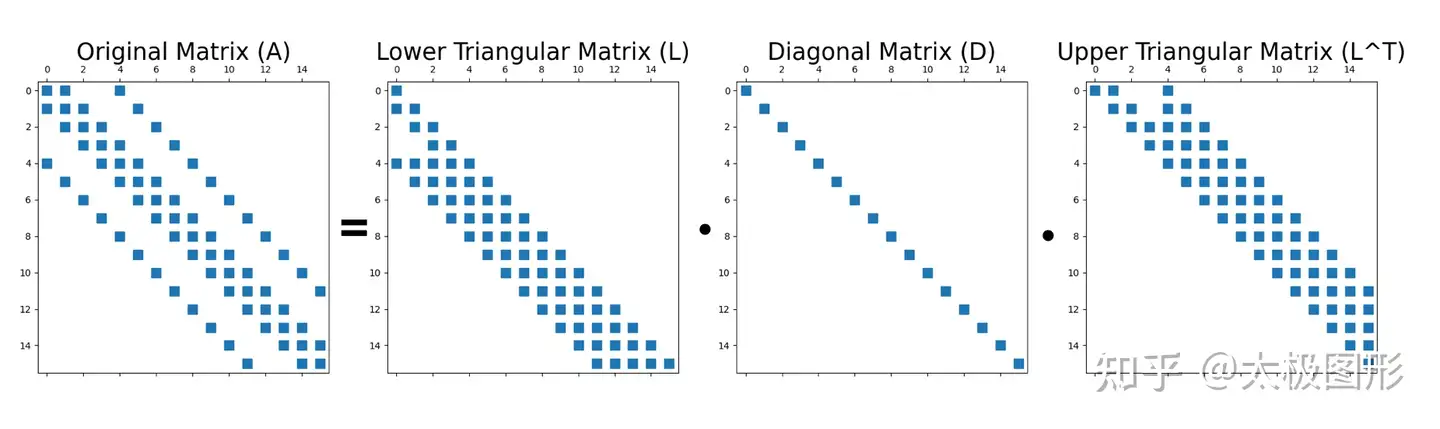
- **LU 分解：**将矩阵分解为下三角矩阵和上三角矩阵，再求解。

#### 2.2.2 迭代求解法

迭代求解法通过不断迭代逼近精确解，常见的迭代求解法有：

- **雅可比迭代法：**每次迭代更新一个元素，直到满足收敛条件。
- **高斯-赛德尔迭代法：**每次迭代更新多个元素，使用前一次迭代的结果。
- **共轭梯度法 (CG)：**一种快速收敛的迭代法，适用于正定矩阵。

### 代码块：稀疏矩阵的创建和存储

% 创建一个稀疏矩阵
A = sparse(3, 4, [1, 2, 3, 4], [1, 3, 2, 4], [5, 6, 7, 8]);

% 查看稀疏矩阵的结构
spy(A)

% 查看稀疏矩阵的存储格式
whos A

**逻辑分析：**

* `sparse` 函数用于创建稀疏矩阵，参数分别为行数、列数、非零元素值、行索引、列索引。
* `spy` 函数可视化稀疏矩阵的结构，非零元素显示为黑色点。
* `whos` 函数显示稀疏矩阵的存储格