MATLAB求解方程组：非线性最小二乘法，数据拟合的终极指南

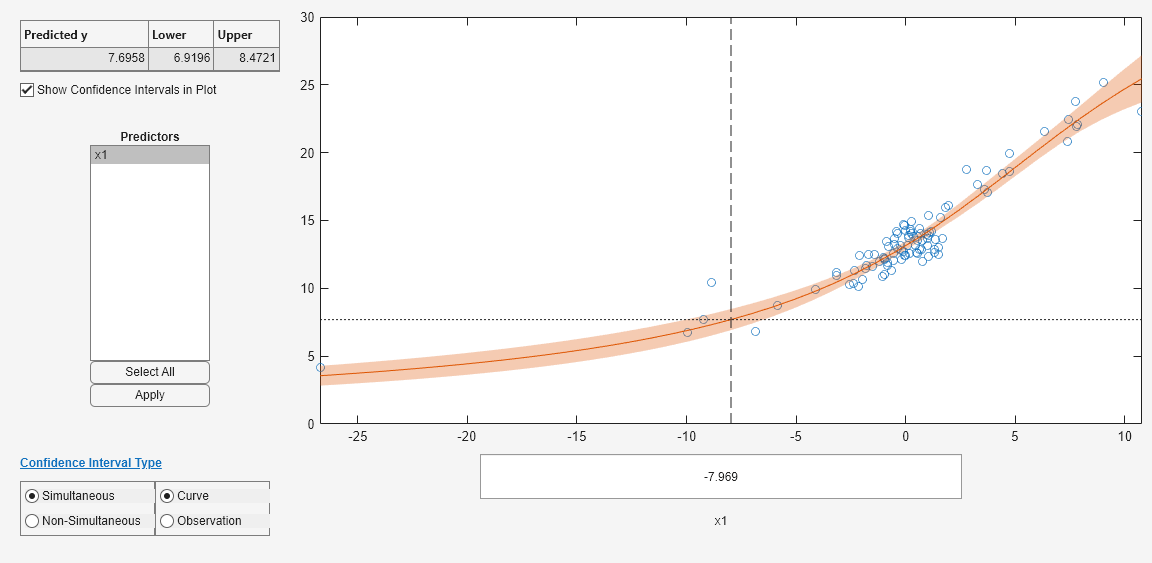
# 1. MATLAB求解方程组概述

MATLAB是一款强大的科学计算软件，它提供了丰富的求解方程组的方法，包括线性方程组和非线性方程组。本章将重点介绍MATLAB求解非线性方程组的方法，包括非线性最小二乘法。

非线性最小二乘法是一种优化方法，用于寻找一组参数，使一个目标函数最小化。它广泛应用于数据拟合、参数估计和模型校准等领域。MATLAB提供了多种非线性最小二乘法求解器，例如lsqnonlin、fminsearch和fminunc，可以根据不同的问题选择最合适的求解器。

# 2. 非线性最小二乘法理论基础

### 2.1 非线性最小二乘法原理

非线性最小二乘法（NLS）是一种优化算法，用于解决非线性方程组。其目标是找到一组参数，使目标函数（即误差平方和）最小化。目标函数通常定义为：

f(x) = 1/2 * ||F(x)||^2

其中：

* `x` 是待求的参数向量
* `F(x)` 是非线性方程组，其元素表示模型与观测值之间的残差

### 2.2 优化算法简介

NLS 算法通过迭代更新参数向量 `x` 来最小化目标函数。常用的优化算法包括：

#### 2.2.1 梯度下降法

梯度下降法沿目标函数梯度方向更新参数，即：

x_new = x_old - α * ∇f(x_old)

其中：

* `α` 是学习率
* `∇f(x)` 是目标函数的梯度

#### 2.2.2 牛顿法

牛顿法使用目标函数的二阶导数（Hessian 矩阵）来更新参数，即：

x_new = x_old - H(x_old)^-1 * ∇f(x_old)

其中：

* `H(x)` 是目标函数的 Hessian 矩阵

#### 2.2.3 共轭梯度法

共轭梯度法是一种迭代算法，它通过构建目标函数的共轭梯度方向来更新参数。该算法通常比梯度下降法收敛得更快。

# 3.1 非线性最小二乘法函数介绍

MATLAB 中提供了 `lsqnonlin` 函数用于求解非线性最小二乘问题。该函数的语法格式如下：

[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(fun,x0,lb,ub,options)

其中：

* `fun`：目标函数，即需要最小化的函数。该函数必须接受一个列向量作为输入，并返回一个标量作为输出。
* `x0`：初始猜测解，即优化算法的起点。
* `lb`：下界，指定每个参数的最小允许值。
* `ub`：上界，指定每个参数的最大允许值。
* `options`：优化选项，用于控制优化算法的行为。

`lsqnonlin` 函数返回以下输出：

* `x`：优化后的解。
* `resnorm`：残差范数，即最小化目标函数后的残差平方和。
* `residual`：残差向量，即目标函数在优化后的解处的值。
* `exitflag`：退出标志，表示优化算法是否成功收敛。
* `output`：优化输出结构，包含有关优化过程的信息。
* `lambda`：拉格朗日乘子向量。
* `jacobian`：雅可比矩阵，即目标函数对参数的导数矩阵。

### 3.2 优化算法的选择和参数设置

`lsqnonlin` 函数支持多种优化算法，包括：

* `'levenberg-marquardt'`：列文伯格-马夸特算法，适用于小规模问题和非线性程度较低的问题。
* `'trust-region-reflective'`：信赖域反射算法，适用于中等规模问题和非线性程度较高的问题。
* `'trust-region-dogleg'`：信赖域狗腿算法，适用于大规模问题和非线性程度较高的问题。

优化算法的选择取决于问题的规模和非线性程度。对于