贝叶斯优化在神经网络中的应用：超参数调优的高级策略

# 1. 贝叶斯优化简介与理论基础

## 1.1 贝叶斯优化的定义与起源
贝叶斯优化是一种高效的全局优化算法，特别适用于目标函数的求解过程既昂贵又难以精确计算的情况。其核心思想是构建目标函数的概率模型，并基于此模型来选择下一次评估的目标函数参数，以期在有限的评估次数下找到最优解。该方法由Herbrich等学者在2000年提出，并逐渐发展成为机器学习领域调参的热门技术之一。

## 1.2 为什么选择贝叶斯优化
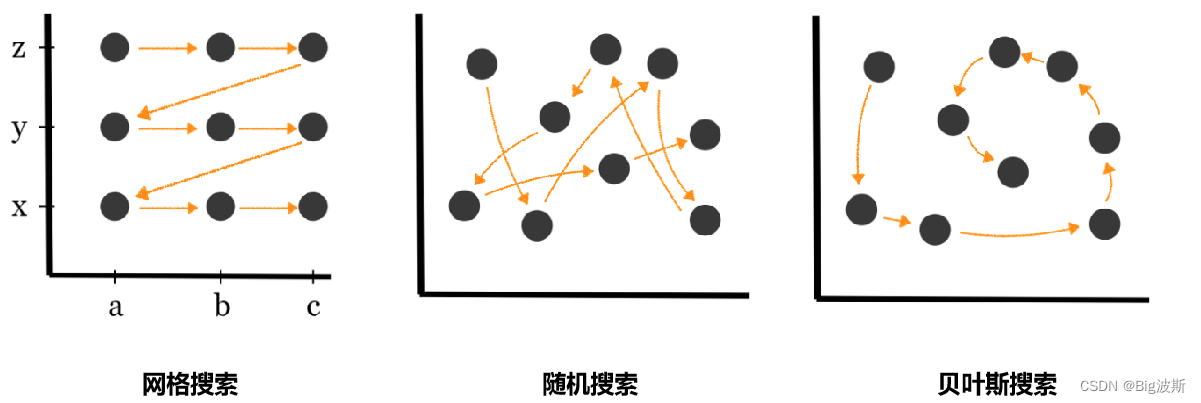
贝叶斯优化之所以受到关注，是因为它通过概率模型的引入，能在探索未知区域和利用已知信息间找到良好的平衡。特别是当目标函数极为复杂或高维时，传统的优化方法如网格搜索或随机搜索将变得低效，贝叶斯优化却能在相同甚至更少的函数评估次数下，寻找到更为精确的全局最优解。这在资源受限的环境下具有极大的优势。

## 1.3 贝叶斯优化的数学基础
贝叶斯优化的基础是贝叶斯理论，其核心是使用贝叶斯公式来计算后验概率，并根据后验概率来指导优化过程。在应用中，通常选择高斯过程（Gaussian Process，GP）作为目标函数的代理模型，因为它可以提供关于未知函数的不确定性估计，并允许方便地计算期望改进（Expected Improvement，EI）等指标，从而在每次迭代中选择最有希望的参数配置。接下来的章节，我们将深入探讨贝叶斯优化的理论细节和实践应用。

# 2. 贝叶斯优化原理深度解析

## 2.1 贝叶斯优化的工作流程

贝叶斯优化是一种高效的全局优化算法，它通过建立目标函数的代理模型来智能地选择采样点，以此来最小化目标函数的评估次数。整个工作流程可以概括为以下几个步骤。

### 2.1.1 目标函数与适应度评估

在开始贝叶斯优化之前，首先需要明确目标函数。目标函数是在给定参数下的性能指标，如在超参数调优中，目标函数可以是验证集上的模型准确率。适应度评估是目标函数的评估过程，通常较为耗时，尤其是涉及复杂的模型训练与验证过程时。

在实际操作中，需要对目标函数进行多次评估，每次评估都会获得一组输入参数和对应的目标函数值（适应度值）。这些数据将用来构建概率模型，以预测未评估点的适应度。

# 假设以下为一个简单的适应度评估函数示例，用于测试贝叶斯优化算法
def fitness_function(params):
    """
    params: 超参数字典，例如：{'learning_rate': 0.01, 'epochs': 50}
    return: 模型在验证集上的准确率
    """
    # 模拟一个耗时的模型训练与评估过程
    accuracy = mock_train_and_evaluate_model(params)
    return accuracy

# 参数示例，这可能是一个由贝叶斯优化算法自动选取的参数组合
example_params = {'learning_rate': 0.03, 'epochs': 30}
# 进行适应度评估
example_accuracy = fitness_function(example_params)

### 2.1.2 概率模型的选择与构建

贝叶斯优化的核心在于使用概率模型来近似目标函数。通常选用高斯过程（Gaussian Process, GP）作为代理模型。GP是一种非参数概率模型，适用于近似任意形状的函数，同时还能给出预测值的不确定性估计。

构建GP模型需要输入先前评估的参数和适应度值，以及根据这些数据拟合出的均值函数和协方差函数。这里需要注意的是，GP的性能很大程度上取决于所选核函数（kernel function），核函数定义了样本点之间的相似性。

### 2.1.3 采样策略与探索与利用权衡

采样策略是决定下一个评估点的重要因素。贝叶斯优化采用一种基于期望改进（Expected Improvement, EI）的策略，它综合考虑了当前最佳已知值和预测值的不确定性，使得采样点既能够探索新的区域，也能够利用现有的最佳发现。

在EI策略中，会计算每个未评估点的EI值，然后选择EI值最高的点作为下一个采样点。这个过程体现了探索与利用之间的权衡，即在尚未充分探索的区域寻找改进的可能性，同时也要考虑到已知的最优点，以期获得更高的适应度值。

## 2.2 贝叶斯优化的关键算法

### 2.2.1 Gaussian过程回归（GPR）

GPR是一种灵活的机器学习方法，它能够预测连续变量，并给出预测结果的不确定性评估。GPR模型由均值函数和协方差函数组成。均值函数描述了函数的中心趋势，而协方差函数则定义了数据点之间的关系。

GPR的核心在于定义一个合适的核函数，它决定了模型预测的平滑程度和依赖距离。常见的核函数包括平方指数核、Matérn核等。选择合适的核函数是GPR模型成功的关键。

### 2.2.2 期望改进（EI）函数

期望改进是一种常用的采样策略，它基于当前最佳已知值和对目标函数的预测来决策。EI函数考虑了函数值的不确定性，赋予改进潜力较大的区域更高的权重。

在实现EI策略时，需要对目标函数值的分布进行采样，计算每个采样点的改进概率，然后计算期望改进值。选择期望改进最大的点作为下一个采样点。

### 2.2.3 非参数化优化方法

贝叶斯优化通过非参数化方法来构建目标函数的近似模型，这使得算法能够处理复杂的、非线性的目标函数。非参数化方法的一个显著优点是它不需要事先定义模型的复杂度，而是通过数据来学习模型。

非参数化优化方法的一个挑战是如何处理高维空间问题。随着参数数量的增加，目标函数的搜索空间急剧增大，这会使得模型的训练和预测变得更加复杂和耗时。

## 2.3 贝叶斯优化的理论挑战与应对

### 2.3.1 高维空间问题

在高维空间中，贝叶斯优化面临着所谓的“维度的诅咒”。维数增加导致样本点间的距离变大，因此需要大量的采样点来覆盖整个空间，这会显著增加优化过程的时间成本。

应对高维空间问题的一种方法是降维，通过特征选择或者使用主成分分析（PCA）等技术来减少模型的维度。此外，还可以通过采用特定的核函数，比如自动相关性确定（ARD）核，来增加模型对高维空间的适应性。

### 2.3.2 全局最优与局部最优的平衡

贝叶斯优化通常旨在找到全局最优解，但有时算法可能会在局部最优解附近徘徊，尤其是在目标函数含有多个局部极值时。为了平衡全局搜索与局部搜索，可以通过调整EI函数中的参数来控制对新区域的探索与对已知好区域的利用。

### 2.3.3 并行化贝叶斯优化

传统的贝叶斯优化是顺序的，即一次只评估一个点。但是，可以通过并行化来显著提高优化过程的效率。并行化贝叶斯优化的挑战在于如何有效地管理和分配计算资源，以及如何同步多个优化过程。

并行化通常涉及同时评估多个候选点，并使用集合中的最佳值来更新代理模型。在实际操作中，可以采用多臂老虎机（Multi-Armed Bandit）等策略来分配资源，并将多个评估点的结果合并以构建更准确的代理模型。

通过本章的介绍，我们深入理解了贝叶斯优化的原理和关键算法，以及在实际应用中可能遇到的挑战及其解决方案。在下一章中，我们将探索贝叶斯优化在神经网络超参数调优中的具体应用，并分析其效果和优势。

# 3. 神经网络超参数调优实践

在前几章节中，我们深入了解了贝叶斯优化的理论基础和原理，并探讨了它的关键算法。现在，让我们将理论付诸实践，专注于如何在神经网络超参数调优中应用贝叶斯优化策略。

## 3.1 神经网络超参数概览

### 3.1.1 超参数的类型与作用

神经网络由多种超参数组成，它们控制着学习过程和网络的结构。超参数可以分为两大类：一类是决定网络结构的参数，如层数、每层的单元数；另一类是控制训练过程的参数，如学习率、批次大小等。超参数的选择直接影响到模型的性能，包括泛化能力、训练速度和是否容易过拟合。

- **网络结构参数**：决定神经网络的基本形态，如层数（网络深度）、每层的神经元数量、激活函数、连接方式（全连接、卷积等）。
- **学习过程参数**：控制训练算法的细节，如学习率、优化器的选择、批次大小（batch size）、损失函数等。

### 3.1.2 超参数对神经网络性能的影响

超参数的选择和调整是一个复杂的问题，因为不同的超参数之间可能存在相互作用，而且某些超参数对模型性能的影响是非线性的。例如，学习率和批次大小直接影响梯度下降的稳定性和收敛速度。一般来说，一个较小的批次大小有助于模型获得更稳定的梯度估计，但过小的批次大小可能会增加训练的方差并降低收敛速度。

## 3.2 贝叶斯优化在超参数调优中的应用

### 3.2.1 贝叶斯优化的步骤与工具

在神经网络超参数调优中，贝叶斯优化的步骤包括定义目标函数、选择概率模型、初始化采集函数，并在每一步迭代中更新概率模型并选择新的超参数配置进行评估。

- **定义目标函数**：目标函数通常是验证集上的损失函数，用以评估超参数配置的好坏。
- **选择概率模型**：Gaussian过程（GP）是贝叶斯优化中常用的一个概率模型，它为黑盒函数的未知性质提供了先验分布。
- **采集函数的选择**：常用的采集函数有期望改进（EI）、概率改进（PI）等，它们利用GP模型给出的概率预测和置信区间。

接下来，我将展示一个简单的代码块，演示如何使用Python中的`scikit-optimize`库来实现贝叶斯优化。

from skopt import BayesSearchCV
from skopt.space import Real, Categorical, Integer
from sklearn.datasets import load_iris
from sklearn.svm import SVC

# 加载数据集
X, y = load_iris(return_X_y=True)

# 设置超参数空间
search_space = {
    'C': Real(1e-6, 1e+6, prior='log-uniform'),
    'gamma': Real(1e-6, 1e+1, prior='log-uniform'),
    'kernel': Categorical(['linear', 'rbf'])
}

# 初始化贝叶斯优化的搜索器
opt = BayesSearchCV(SVC(), search_space, n_iter=32, random_state=0)

# 开始优化过程
opt.fit(X, y)

# 输出最优超参数
print("最优超参数：", opt.best_params_)

在此代码块中，我们使用了`scikit-optimize`库中的`BayesSearchCV`类，它是一个封装了交叉验证的贝叶斯优化器。我们定义了支持向量机（SVM）的超参数空间，并通过`fit`方法开始优化过程。优化完成后，可以通过`opt.best_params_`获取到最优的超参数配置。

### 3.2.2 超参数空间的定义与采样

定义超参数空间时，需要指定每个超参数的取值范围和类型。对于数值型的超参数，我们通常使用`Real`或`Integer`类型，它们允许我们指定参数值的上下界以及是否采用对数先验。对于分类型的超参数，则使用`Categorical`类型。

在采样过程中，贝叶斯优化通常不会随机地从超参数空间中采样，而是利用之前评估的超参数点来指导后续的采样决策。这通过更新概率模型和重新选择采集函数来实现。

### 3.2.3 实际案例分析

让我们分析一个使用贝叶斯优化来调整神经网络超参数的实例。

假设我们有一个基于卷积神经网络（CNN）的图像分类任务，我们的目标是优化网络的深度、学习率和批次大小等超参数。我们将使用`Hyperopt`这个库来执行超参数优化过程。

from hyperopt import hp, fmin, tpe, Trials, STATUS_OK
from keras.models import Sequential
from keras.layers import Dense, Conv2D, Flatten
from keras.datasets import mnist
from keras.utils import to_categorical

# 加载MNIST数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(-1, 28, 28, 1) / 255.0
x_test = x_test.reshape(-1, 28, 28, 1) / 255.0
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)

# 定义超参数空间
spac