【禁忌搜索法】：神经网络超参数调优的高级技巧

# 1. 禁忌搜索法简介及其在优化问题中的应用

## 1.1 禁忌搜索法的起源与核心理念
禁忌搜索法（Tabu Search, TS）是现代启发式搜索算法的一种，起源于1980年代，由Fred Glover提出，用以解决复杂优化问题。其核心理念在于避免搜索陷入局部最优解，并通过建立禁忌表来记录已经访问过的解，从而指导搜索过程向未探索的区域前进。通过对解空间的智能搜索，禁忌搜索法能够有效找到高质量的全局最优解或近似最优解。

## 1.2 禁忌搜索法的操作步骤与特点
禁忌搜索法的操作步骤包括初始化解、定义邻域结构、设定禁忌表以及迭代更新解。在每一步迭代中，算法从当前解的邻域中选择一个解作为候选解，并根据事先定义的评价准则（如适应度函数）来确定是否接受该候选解。值得注意的是，即使候选解的质量优于当前解，如果它被禁忌表所禁止，算法也可能拒绝它，以此来跳出局部最优解的陷阱。禁忌搜索法的特点是操作简单，但能有效处理大规模优化问题，具有广泛的适用性和高效的搜索能力。

## 1.3 禁忌搜索法在优化问题中的应用场景
在实际应用中，禁忌搜索法广泛应用于旅行商问题（TSP）、调度问题、生产计划、路径规划等各类组合优化问题。由于其优异的搜索性能，禁忌搜索法同样适用于机器学习中的超参数调优，比如神经网络的结构和权重参数优化。它能够帮助工程师在复杂的参数空间中找到更优的模型配置，从而提升模型的性能。接下来的章节中，我们将深入探讨禁忌搜索法的理论基础与实践应用，以及如何在超参数调优中运用该方法。

# 2. 神经网络基础知识与超参数概念

### 2.1 神经网络的组成与工作原理

神经网络是由大量的节点（或称神经元）彼此之间相互连接构成的网络。这些节点通常被组织成不同的层，每层包含一组神经元，它们共同负责处理信息的不同方面。理解神经网络的工作原理对于任何从事机器学习或深度学习工作的IT专家来说是至关重要的。

#### 2.1.1 神经网络的层和类型

神经网络由多种类型的层组成，包括输入层、隐藏层以及输出层。每一层中的神经元根据其在网络中的位置执行特定的任务。输入层接收初始数据，隐藏层（一个或多个）处理并提取特征，输出层根据前一层的计算结果产生最终的输出。

在众多类型的神经网络中，最常见的是全连接层（Fully Connected Layers）、卷积层（Convolutional Layers）和循环层（Recurrent Layers）。全连接层的神经元与上一层的所有神经元都相连。卷积层通常用于处理图像数据，通过卷积操作从输入数据中提取空间特征。循环层则用于处理序列数据，能够保存前面时间点的信息，从而捕捉数据的时序特性。

# 示例代码展示一个简单的全连接神经网络层（使用Keras库）
from keras.layers import Dense
from keras.models import Sequential

model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_size,)))
model.add(Dense(64, activation='relu'))
model.add(Dense(output_size, activation='softmax'))

***pile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

在上述代码中，`Dense`层表示全连接层，`input_shape`定义了输入数据的形状，`activation`定义了激活函数类型，如ReLU或softmax。

#### 2.1.2 前向传播和反向传播机制

前向传播是指数据通过网络从输入层到输出层流动的过程。在每一层中，神经元会对输入信号进行加权求和，并通过一个激活函数产生输出。反向传播算法的核心是在网络训练过程中调整权重参数，以便减少输出层的预测误差。它通过计算损失函数相对于权重的梯度，利用链式法则依次反向更新每一层的权重。

# 示例代码展示了反向传播的梯度计算（假设已有的损失函数loss）
import numpy as np

def backward_pass(y_true, y_pred):
    return np.subtract(y_true, y_pred)  # 计算预测误差，即梯度的起点

# 假设y_true是真实标签，y_pred是模型的预测
# 此处仅为演示，实际中会使用更复杂的梯度计算方式

### 2.2 神经网络超参数的作用和分类

超参数是那些在训练之前设定好的参数，它们控制着学习过程本身。这些参数不会在学习过程中被直接学习或调整。下面详细探讨了其中一些重要的超参数。

#### 2.2.1 学习率、批量大小和迭代次数

学习率（Learning Rate）决定了在梯度下降过程中参数更新的幅度。太小的学习率会导致学习过程缓慢，而太大的学习率可能导致模型无法收敛。批量大小（Batch Size）是指一次训练过程中使用多少样本。一个较小的批量大小能够提供更频繁的权重更新，通常有助于收敛，但计算成本较高。迭代次数（Iterations）是指整个训练集完整通过神经网络一次的次数。

# 示例代码展示了如何在训练时设置学习率、批量大小和迭代次数
from keras.optimizers import Adam

optimizer = Adam(learning_rate=0.001)
***pile(optimizer=optimizer, loss='categorical_crossentropy', metrics=['accuracy'])

history = model.fit(X_train, y_train, batch_size=32, epochs=100)

在上述代码中，`Adam`优化器被用来设置学习率为0.001。`fit`方法中`batch_size`被设置为32，`epochs`为100，表示模型将使用32个样本的批量大小进行训练，整个训练过程将持续100次迭代。

#### 2.2.2 权重初始化和激活函数选择

权重初始化（Weight Initialization）是指在训练之前给神经元权重赋一个初始值的过程。不恰当的初始化可能导致训练效率低下或模型无法学习。常见的权重初始化方法有零初始化（Zero Initialization）、随机初始化（Random Initialization）和Xavier初始化。激活函数（Activation Functions）如ReLU、Sigmoid或Tanh则用于为神经网络引入非线性因素，使得网络能够捕捉复杂的数据结构。

# 示例代码展示如何设置权重初始化和激活函数
from keras.initializers import GlorotUniform
from keras.layers import Dense

def build_model():
    model = Sequential()
    model.add(Dense(128, activation='relu', kernel_initializer=GlorotUniform()))
    model.add(Dense(64, activation='relu', kernel_initializer=GlorotUniform()))
    model.add(Dense(output_size, activation='softmax'))
    ***pile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
    return model

model = build_model()

在上面的代码中，`GlorotUniform`初始化方法被用来初始化权重。选择`relu`作为激活函数，因为它是当前深度学习实践中最为常用和有效的选择之一。

### 2.3 神经网络超参数调优的必要性

超参数的选择对于神经网络的性能有着直接的影响。在本节中，我们将探讨超参数如何影响模型的性能，以及超参数调优的常见方法。

#### 2.3.1 超参数对模型性能的影响

不同的超参数设置会导致模型在收敛速度、准确度和泛化能力上有显著的差异。例如，学习率设置不当可能导致模型学习速度过慢或震荡；批量大小的选择会影响到内存的使用效率以及训练的稳定性。

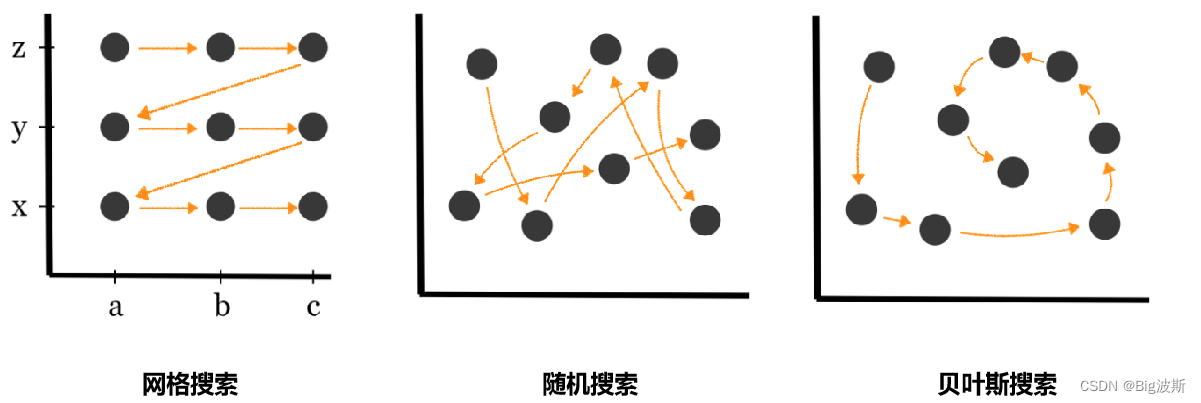
#### 2.3.2 超参数调优的常见方法比较

超参数调优最基础的方法是手动调整，这种方法在小规模的项目中比较适用，但在复杂系统中非常耗时。网格搜索（Grid Search）和随机搜索（Random Search）是更为系统的方法。它们通过在预设的超参数空间中搜索最优的组合，尽管效率仍然不高。进化算法（Evolutionary Algorithms）和贝叶斯优化（Bayesian Optimization）是更高级的调优方法，它们通过建立性能与超参数之间的模型来指导搜索过程，能够更加高效地找到优化的超参数组合。

以上内容仅是本章节的概述，详细内容将在后续章节中逐一展开，为读者提供深入且实用的超参数调优技术。

# 3. 禁忌搜索法的理论基础与实现机制

## 3.1 禁忌搜索法的算法原理

### 3.1.1 禁忌搜索法的基本概念

禁忌搜