【统计方法在超参数调优中的应用】：深度学习的精确度量

# 1. 超参数调优的基础知识

## 1.1 超参数调优简介
在机器学习和深度学习中，超参数调优是一个关键环节，其目的是找到最佳的超参数设置，使得模型能够在未知数据上获得最佳性能。超参数不同于模型的参数，它们不能通过训练数据直接学习得到，需要手动设置和优化。超参数的范围很广，包括学习率、批次大小、隐藏层数量等。

## 1.2 超参数的重要性
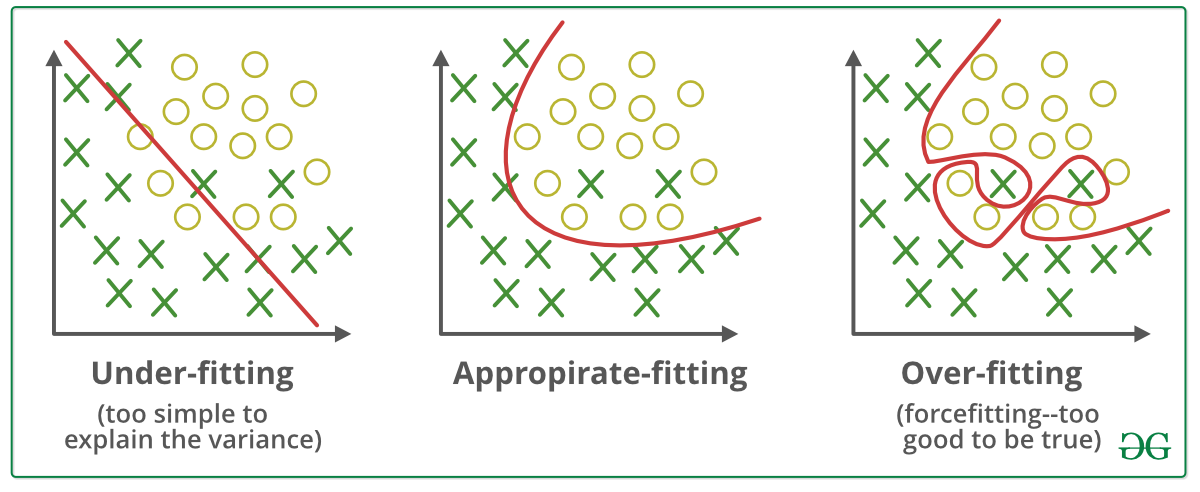
超参数的设置直接影响到模型的学习效率和泛化能力。如果超参数设置不当，可能会导致模型无法学习到数据中的有效模式，或者导致过拟合现象，即模型在训练数据上表现良好，但在新数据上表现不佳。

## 1.3 基本的超参数调优方法
最简单的超参数调优方法是手动尝试不同的参数组合，这通常称为“试错法”。然而，这种方法效率低下，不适合处理高维超参数空间。因此，研究人员开发了多种自动化超参数调优技术，如网格搜索、随机搜索、贝叶斯优化等，以提高超参数搜索的效率和效果。

# 示例代码：使用网格搜索进行超参数调优
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier

# 假设我们有一个随机森林分类器和一些训练数据
rf = RandomForestClassifier()
parameters = {'n_estimators': [10, 50, 100], 'max_depth': [2, 5, 10]}
clf = GridSearchCV(rf, parameters, scoring='accuracy')

# 训练模型并找到最佳参数组合
clf.fit(X_train, y_train)
best_params = clf.best_params_
print("Best parameters found: ", best_params)

本章为超参数调优的入门介绍，后续章节将深入探讨统计方法在超参数调优中的应用，帮助读者从理论和实践两方面提高调优技能。

# 2. 统计方法的基本原理

### 2.1 统计学在数据分析中的角色

统计学是数据分析的基石，它提供了一套强大的工具和方法，帮助我们从数据中提取有价值的信息，理解数据的内在结构，并做出合理的推断和决策。在这一部分，我们将探讨统计学如何应用于数据分析，以及它在超参数调优中所扮演的关键角色。

#### 2.1.1 数据分布的理解与应用

在分析任何数据集之前，理解数据的分布是至关重要的一步。数据分布描述了数据是如何围绕其平均值或中心值分布的。常见的数据分布包括正态分布、均匀分布、二项分布等。掌握这些分布的特点能够帮助我们做出更好的预测和决策。

以正态分布为例，它广泛应用于自然和社会科学中，因为许多自然现象和社会现象产生的数据遵循这种分布。在机器学习中，许多算法假设数据是正态分布的，或者至少接近正态分布。例如，逻辑回归模型假设数据服从逻辑斯蒂分布，其形状类似于正态分布。

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布数据
data = np.random.normal(0, 1, 1000)

# 绘制直方图
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')

# 绘制正态分布曲线
mu, std = data.mean(), data.std()
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = 1 / (std * np.sqrt(2 * np.pi)) * np.exp(- (x - mu)**2 / (2 * std**2))
plt.plot(x, p, 'k', linewidth=2)

plt.title("Normal Distribution")
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

在上述代码中，我们生成了一组正态分布的随机数据，并绘制了其直方图和理论上的正态分布曲线。通过这个可视化，我们可以直观地理解数据是如何围绕其平均值分布的。

#### 2.1.2 假设检验的基本步骤与意义

假设检验是统计推断的核心，它允许我们根据有限的数据对总体参数做出推断。在超参数调优中，假设检验可以用来验证模型的改进是否具有统计学意义，即是否不太可能是由随机变化引起的。

假设检验一般包括以下几个步骤：
1. 建立零假设（H0）和备择假设（H1），通常零假设表明没有效应或差异，备择假设表明有效应或差异。
2. 计算检验统计量，如t统计量、F统计量或卡方统计量。
3. 确定显著性水平（alpha），这是犯第一类错误（拒绝真实零假设）的概率上限。
4. 根据检验统计量和显著性水平决定是否拒绝零假设。

假设检验的意义在于，它提供了一种系统的方法来评估观测到的结果是否可能由随机性引起。在机器学习模型的上下文中，我们经常使用假设检验来确定我们的超参数调整是否导致了性能的显著提升。

### 2.2 关键统计概念在超参数调优中的应用

在超参数调优的过程中，某些统计概念尤为重要。理解这些概念不仅可以帮助我们更好地选择超参数，还可以帮助我们预测模型在新数据上的表现。

#### 2.2.1 置信区间在参数估计中的重要性

当我们对数据进行分析时，我们通常需要估计模型参数的值。置信区间提供了一个范围，该范围内有一定概率包含真实参数的值。例如，一个95%的置信区间意味着，如果我们重复实验多次，其中95%的实验结果的真实参数值将落在这个区间内。

在超参数调优中，置信区间可以帮助我们评估超参数的调整是否有效，以及调整的超参数是否在统计上显著改善了模型性能。

from scipy import stats

# 假设的性能度量样本数据
performance_sample = np.random.normal(0, 1, 30)

# 计算95%置信区间
mean = np.mean(performance_sample)
std_err = stats.sem(performance_sample)
conf_interval = stats.t.interval(0.95, len(performance_sample) - 1, mean, std_err)

print("95%置信区间: ({:.2f}, {:.2f})".format(conf_interval[0], conf_interval[1]))

在上面的代码中，我们使用样本均值和标准误差来计算并打印出95%置信区间。通过这种方式，我们可以量化不确定性和评估参数的可信度。

#### 2.2.2 A/B测试在模型比较中的使用

A/B测试是对比两种模型或策略的一种常用方法，通过将用户随机分为两组，一组使用模型A，另一组使用模型B，然后比较两组的性能指标，如点击率、转化率或任何相