【生物信息学中的应用】：支持向量机在基因表达数据分析中的威力！

# 1. 生物信息学与基因表达数据概述

## 生物信息学简介
生物信息学是一个跨学科的领域，它结合了生物学、计算机科学、统计学、数学和工程学等多个学科的知识，用以处理和分析生物学数据。该领域的一个核心任务是解读和管理基因组、蛋白质组以及其他类型的生物分子数据。

## 基因表达数据的意义
基因表达数据是生物信息学中的关键数据类型之一，它反映了在不同条件下，基因表达其功能产物——通常是mRNA或蛋白质的水平。这些数据对于理解生命活动过程、疾病机理以及药物作用等方面具有重要意义。

## 数据分析工具的重要性
为了从这些复杂的数据中提取有用的信息，需要借助先进的数据分析工具和算法。支持向量机（SVM）作为一种强大的机器学习算法，在基因表达数据分析中扮演着重要角色。通过本章的介绍，我们将为后续章节的深入探讨打下基础。

# 2. 支持向量机理论基础

## 2.1 支持向量机的基本概念

### 2.1.1 统计学习与机器学习的关系

统计学习和机器学习是两个密切相关但又有所区别的概念。统计学习强调通过统计方法从数据中学习模式和结构，而机器学习则更多地强调在计算机程序中实现自动学习和泛化能力。支持向量机（SVM）作为一种分类器，其核心是寻找数据的最优分割边界，这背后的理论基础来源于统计学习领域，但其应用和实现更多体现在机器学习的范畴。

在构建SVM模型时，我们通常需要确定一个最优的分类边界，这个边界能够将不同类别的数据以最大间隔分开。这个间隔的计算基于统计学中的间隔最大化原理，而模型的训练和验证则涉及大量计算和优化过程，这正是机器学习的典型应用。

### 2.1.2 支持向量机的数学原理

支持向量机是基于统计学习理论中的结构风险最小化原则构建的。其核心思想是，为了最小化泛化误差，需要在经验风险和置信范围之间找到一个平衡点。SVM通过最大化两个类别数据的间隔来控制模型的复杂度，从而达到良好的推广能力。

数学上，SVM通过构建一个超平面来区分两类数据，超平面的方程形式为 `w*x + b = 0`，其中 `w` 是超平面的法向量，`b` 是偏置项。SVM的目标是最大化两个类别数据点到该超平面的最小距离，即最大化间隔。这可以通过解决一个凸优化问题来实现，该问题在满足数据点正确分类的前提下，最小化 `||w||^2`，也即最大化间隔。

minimize    ||w||^2 / 2
subject to  y_i * (w*x_i + b) >= 1,  i=1,...,N

其中 `y_i` 是第 `i` 个数据点的类别标签，`x_i` 是第 `i` 个数据点的特征向量，N 是数据点的数量。

## 2.2 支持向量机的分类原理

### 2.2.1 最大间隔分类器

SVM的分类原理可以概括为最大间隔分类器。在特征空间中，数据被表示为点，而SVM的目标是找到一个分割超平面，使得最近的数据点（支持向量）到该超平面的距离最大。在二维空间中，这个超平面就是一个直线，而在更高维的空间中，则是一个超平面。

要正确分类所有的数据点，SVM还需要引入松弛变量（slack variables）来处理那些无法完全线性分割的数据。松弛变量允许某些点违反间隔最大化条件，但要为这些违规点支付一定的成本，这通过引入惩罚项 `C * sum(ξ_i)` 到目标函数中来实现，其中 `ξ_i` 是松弛变量，`C` 是惩罚参数。

minimize    ||w||^2 / 2 + C * sum(ξ_i)
subject to  y_i * (w*x_i + b) >= 1 - ξ_i,  i=1,...,N
            ξ_i >= 0,  i=1,...,N

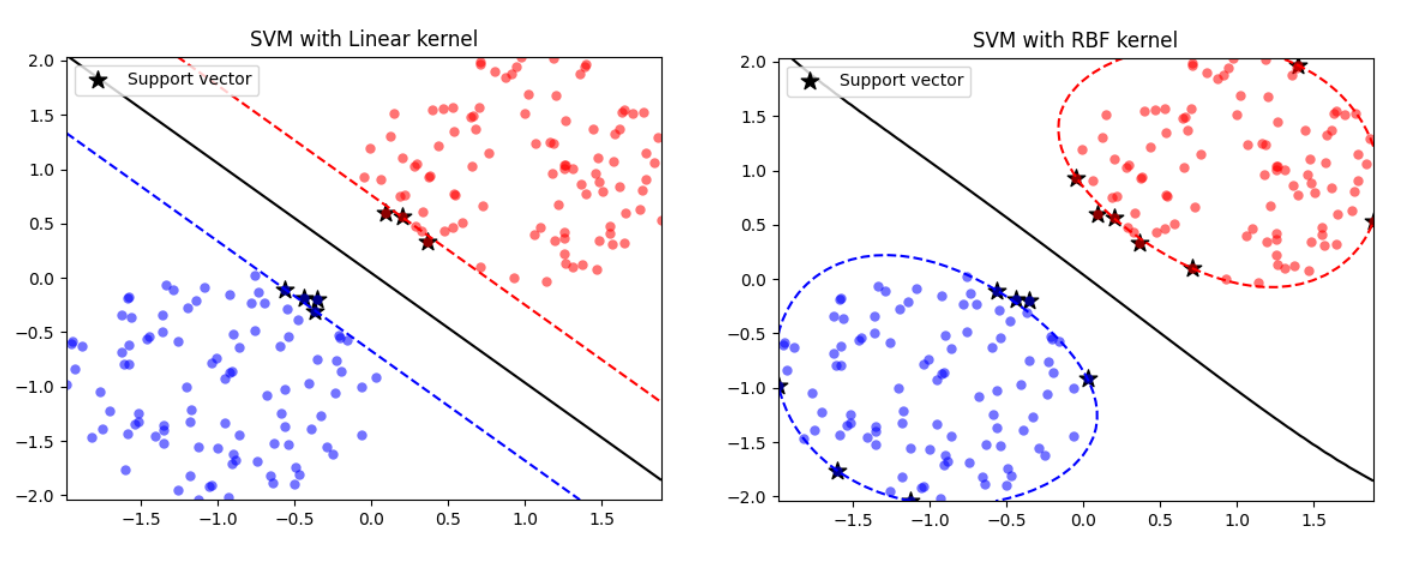
### 2.2.2 核技巧与非线性可分问题

当数据是非线性可分时，即无法用一个线性超平面将两类数据完全分隔开，SVM使用核技巧来解决这一问题。核技巧的核心思想是通过映射将原始数据映射到一个更高维的空间，在这个新空间中数据可能变得线性可分。

核函数（kernel function）允许我们在不显式地计算高维特征空间的情况下，有效地计算高维空间中的点积。常见的核函数包括线性核、多项式核、径向基函数（RBF）核和sigmoid核。选择不同的核函数和相应的参数，可以构建出适用于不同数据集的SVM模型。

## 2.3 支持向量机的优化算法

### 2.3.1 序列最小优化（SMO）算法

序列最小优化算法是SVM训练中的一种有效且常用的方法。SMO算法的基本思想是，将大优化问题分解为一系列最小的优化问题。这些最小问题只需要考虑两个拉格朗日乘数（Lagrange multipliers），因此可以非常快速地解决。

SMO算法的步骤包括选择一对拉格朗日乘数进行优化，并且在优化过程中保持其他乘数不变。通过不断迭代选择和优化对，SMO逐步逼近全局最优解。其优势在于计算复杂度较低，尤其是在支持向量数量较多的情况下，可以显著减少训练时间。

### 2.3.2 软间隔与正则化参数选择

在实践中，很难找到一个超平面完美地将两类数据分开，而且过于严格的要求可能使模型过于复杂，容易过拟合。因此，SVM引入了软间隔的概念，允许一些数据点违反间隔最大化原则。

软间隔通过引入松弛变量来实现，而松弛变量的权重由正则化参数C控制。C的值越小，对间隔违规的容忍度越高，模型的泛化能力越好，但模型的风险也可能增加。选择合适的C值是一个重要的模型选择问题，通常通过交叉验证来确定最佳值。

from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV

param_grid = {'C': [0.1, 1, 10, 100]}
svc = SVC(kernel='rbf')
clf = GridSearchCV(svc, param_grid)
clf.fit(X_train, y_train)
best_params = clf.best_params_
print("Best parameters: ", best_params)

上述代码使用了Scikit-learn库中的SVC（支持向量分类器）和GridSearchCV（网格搜索）来通过交叉验证选择最佳的正则化参数C。

# 3. 基因表达数据分析实践

随着生物信息学的飞速发展，基因表达数据已成为研究者进行疾病机理研究、新药开发以及个性化医疗的重要资源。基因表达数据提供了细胞中基因活性的信息，是生物信息学分析中不可或缺的数据类型。在本章节中，我们将探索如何获取和预处理基因表达数据，并进一步介绍使用支持向量机（SVM）进行分类的实践操作，最后讨论如何进行有效的特征选择。

## 3.1 基因表达数据的获取与预处理

### 3.1.1 数据来源与格式

获取基因表达数据的第一步是确定可靠的数据来源。目前，公共数据库如Gene Expression Omnibus (GEO)、The Cancer Genome Atlas (TCGA)以及ArrayExpress等提供了大量经过同行评议的基因表达数据集。这些数据集通常以CEL、GCT或CSV等格式存储，包含了样本的原始读数、处理后的表达值以及其他注释信息。

### 3.1.2 数据清洗与标准化方法

数据预处理是分析之前必不可少的步骤，包括数据清洗和标准化。数据清洗主要是去除异常值、填补缺失值等。而标准化是将数据统一到相同的比例尺度上，常用的标准化方法包括Z-score标准化、log2变换等。标准化的目的是减少数据分散性，从而提升后续分析的效果。

import numpy as np
from sklearn.preprocessing import StandardScaler

# 示例代码：数据标准化
data = np.array([[2, 4, 1], [5, 3, 2], [2, 2, 4]])
scaler = StandardScaler()
normalized_data = scaler.fit_transform(data)

以上代码使用了Python中的scikit-learn库来执行数据标准化。参数说明为`data`是原始数据集，`StandardScaler()`是scikit-learn中用于数据标准化的类，`fit_transform`方法则结合了拟合（计算均值和标准差）和转换（标准化数据）的过程。

## 3.2 使用支持向量机进行分类

### 3.2.1 构建分类器的步骤

构建SVM分类器通常包括以下步骤：选择合适的核函数、设置C参数（软间隔的正则化参数），然后训练模型。核函数用于处理非线性可分问题，常见的核函数包括线性核、多项式核、径向基函数（RBF）核等。选择合适的核函数