【优化算法：序列最小优化（SMO）】：SVM性能提升的秘密武器解析！

# 1. 序列最小优化（SMO）算法概述

序列最小优化（SMO）算法是一种在支持向量机（SVM）学习中常用的优化技术。本章旨在为读者提供SMO算法的初步认识，并为其在后续章节的深入分析奠定基础。

## 1.1 SMO算法起源与发展

SMO算法由John C. Platt于1998年提出，是解决SVM中二次规划问题的一种高效方法。它将大问题拆分为一系列最小化问题，通过不断选择和优化两个拉格朗日乘子来迭代更新，大大减少了计算复杂度。

## 1.2 SMO算法的核心特点

SMO算法的核心在于其选择和优化两个变量的策略，它允许在没有任何矩阵运算的情况下更新模型，从而提高效率。这种分而治之的方法减少了优化过程中对内存的依赖，并提升了算法的可扩展性。

## 1.3 SMO算法在SVM中的作用

SMO是SVM学习过程中的核心组件，通过将复杂的二次规划问题分解为一系列简单子问题，使得SVM的训练过程得以快速准确地执行。这不仅加快了模型训练的速度，还提高了模型的稳定性和预测精度。

# 2. 支持向量机（SVM）基础

## 2.1 SVM的理论基础

### 2.1.1 最大间隔分类器的数学原理

支持向量机（SVM）是一种二分类模型，其基本模型定义为特征空间中间隔最大化的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也因此从理论上说，得到的将是全局最优点。

在数学上，SVM通过构建一个超平面作为决策边界，以最大化不同类别数据点之间的间隔。对于给定的训练样本集合：

graph TD;
    A[超平面] --> B(分类超平面);
    B --> C{支持向量};
    C --> D(正例);
    C --> E(负例);
    D -.->|间隔| E;

支持向量机的目标是找到一个超平面，使得最近的正例和负例数据点之间的间隔（也称为边缘）最大。这个间隔就是从超平面到最近的任何样本点的距离，数学上可以表示为：

\[
\begin{align*}
& \text{maximize}_{\mathbf{w}, b} \quad \frac{2}{\|\mathbf{w}\|} \\
& \text{subject to} \quad y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1, \quad i = 1, \dots, n
\end{align*}
\]

其中，\(\mathbf{w}\) 是超平面的法向量，\(b\) 是偏置项，\(y_i\) 是类别标签，\(\mathbf{x}_i\) 是特征向量，\(n\) 是样本数。

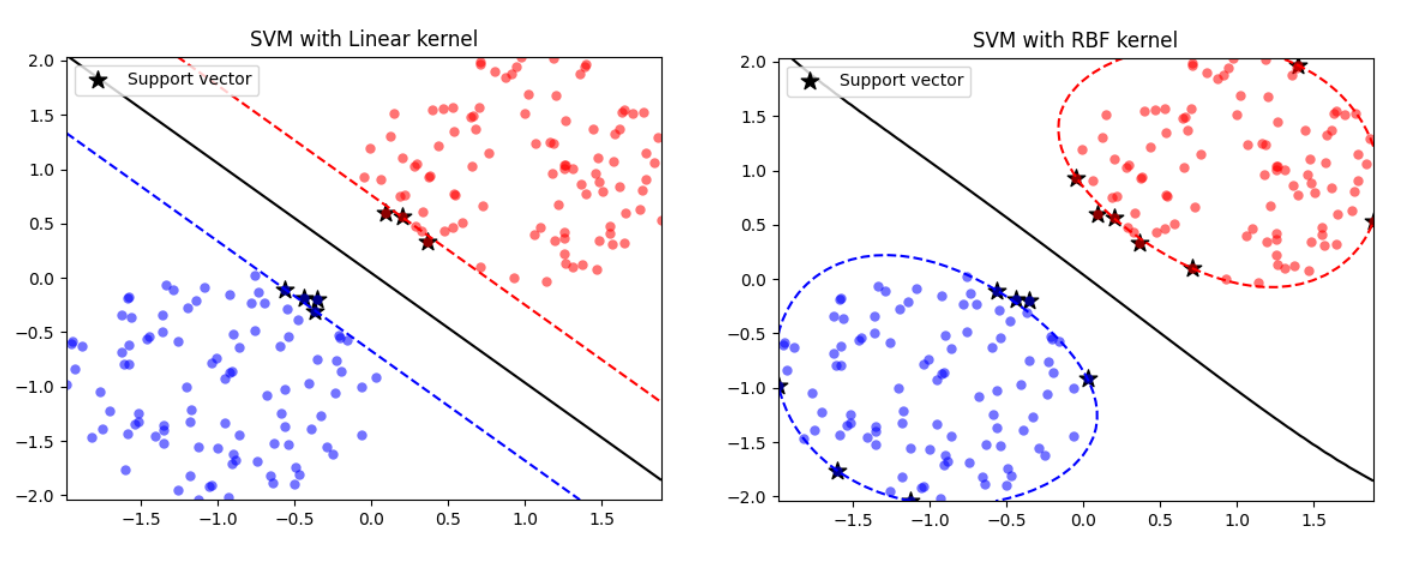
### 2.1.2 核技巧与非线性SVM

在现实世界问题中，数据往往不是线性可分的。为了处理这些问题，核技巧被引入SVM中。核技巧通过一个非线性映射将原始数据映射到一个更高维的空间，使得在这个高维空间中数据是线性可分的。核函数的作用是隐式地在高维空间中进行点积运算，而无需显式地计算映射后的向量，这样可以提高计算效率。

常见的核函数包括：

- 线性核：\( k(\mathbf{x}, \mathbf{z}) = \mathbf{x} \cdot \mathbf{z} \)
- 多项式核：\( k(\mathbf{x}, \mathbf{z}) = (\mathbf{x} \cdot \mathbf{z} + 1)^d \)
- 径向基函数（RBF）核：\( k(\mathbf{x}, \mathbf{z}) = \exp(-\gamma \|\mathbf{x} - \mathbf{z}\|^2) \)
- Sigmoid核：\( k(\mathbf{x}, \mathbf{z}) = \tanh(\alpha \mathbf{x} \cdot \mathbf{z} + c) \)

其中，\(\gamma\), \(d\), \(\alpha\), 和 \(c\) 是核函数的参数，可以调整以优化模型性能。

核函数的选择和参数的调整通常通过交叉验证和网格搜索等方法进行。核技巧允许SVM在高维空间中有效工作，但同时也增加了计算复杂度和过拟合的风险。

## 2.2 SVM的学习与优化目标

### 2.2.1 优化问题的构造

SVM的核心是将线性分类问题转化为一个凸二次规划问题。在构造优化问题时，SVM引入了松弛变量，以允许某些数据点位于分隔超平面的错误一侧。通过松弛变量，优化问题变得更加灵活，能够处理线性不可分的情况。

优化问题的一般形式是：

\[
\begin{align*}
& \text{minimize}_{\mathbf{w}, b, \boldsymbol{\xi}} \quad \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^n \xi_i \\
& \text{subject to} \quad y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 - \xi_i, \quad i = 1, \dots, n \\
& \quad \quad \quad \quad \xi_i \geq 0, \quad i = 1, \dots, n
\end{align*}
\]

这里的 \(C\) 是一个正则化参数，用于平衡模型的复杂度和数据拟合的程度。

### 2.2.2 拉格朗日乘子法基础

为了求解上述优化问题，SVM使用了拉格朗日乘子法。这种方法可以将原问题转换为对偶问题，并且得到的数据点是支持向量，这些支持向量定义了最终的决策边界。

拉格朗日函数定义为：

\[
L(\mathbf{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} \|\mathbf{w}\|^2 - \sum_{i=1}^n \alpha_i [y_i(\mathbf{w} \cdot \mathbf{x}_i + b) - 1]
\]

其中，\(\boldsymbol{\alpha}\) 是拉格朗日乘子向量，每个乘子对应一个训练样本。通过最小化 \(L\) 关于 \(\mathbf{w}\) 和 \(b\) 的值，并最大化关于 \(\boldsymbol{\alpha}\) 的值，可以得到优化问题的对偶问题。

对偶问题为：

\[
\begin{align*}
& \text{maximize}_{\boldsymbol{\alpha}} \quad \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n \alpha_i \alpha_j y_i y_j \mathbf{x}_i \cdot \mathbf{x}_j \\
& \text{subject to} \quad \alpha_i \geq 0, \quad i = 1, \dots