【算法大比拼】：SVM vs. 决策树 vs. 神经网络：谁主沉浮？

# 1. 机器学习算法概述

## 1.1 机器学习的定义与重要性

机器学习是一门让计算机能够从经验中学习的科学，它赋予了计算机自我进步的能力。通过算法对数据进行学习，机器可以识别复杂模式并做出智能决策或预测。在数据驱动的当今世界，机器学习已成为不可或缺的技术，广泛应用于推荐系统、图像识别、语音识别、自然语言处理等领域。

## 1.2 机器学习的主要类别

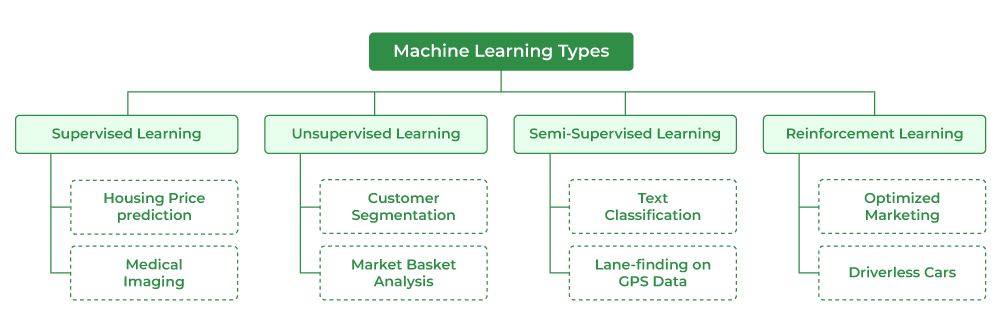
机器学习算法主要分为三种类型：监督学习、无监督学习和强化学习。

- 监督学习通过训练数据中的输入和输出，预测未知数据的输出。
- 无监督学习探索数据中的隐藏结构和模式，没有预定义的标签。
- 强化学习侧重于如何基于环境采取行动以最大化某种累积奖励。

## 1.3 机器学习的工作流程

机器学习的工作流程包括数据预处理、特征工程、模型选择、训练与测试几个关键步骤。其中数据预处理关注清洗和格式化数据，特征工程旨在提取重要特征，模型选择则是根据问题类型和数据特性挑选合适的算法，而训练与测试则涉及模型的拟合和评估。

在随后的章节中，我们将深入探讨支持向量机（SVM）等具体算法的原理、实战应用和优化策略，逐步揭示机器学习的强大功能和实践技巧。

# 2. 支持向量机（SVM）深度解析

支持向量机（SVM）作为机器学习中的一个经典算法，长久以来被广泛研究和应用。其核心思想是寻找一个超平面来对不同类别的数据进行分隔，使得分类间隔最大化。这一原理不仅适用于线性可分的数据，通过引入核技巧，SVM在处理非线性问题上也表现出色。本章节将深入探讨SVM的基本原理、优缺点以及实际应用。

## 2.1 SVM基本原理与数学模型

### 2.1.1 最大间隔分类器的概念

在讲到SVM时，一个关键的概念就是最大间隔分类器。在特征空间中，SVM寻找一个超平面，使不同类别数据间的间隔最大化。在二分类问题中，我们可以将数据表示为特征向量 x，类别标签为 y（+1 或 -1）。SVM的目标是找到一个超平面（即决策边界），满足对于所有的训练样本，其分类边界（间隔）都是最大的。

用数学的语言表达就是，要找到一个向量 w 和偏置 b，使得对于所有的数据点 (x_i, y_i)，都有 y_i(w*x_i + b) ≥ 1。这个几何间隔是由 w 的范数决定的，所以要最大化间隔，等价于最小化 ||w|| 的平方，这可以通过解决一个二次规划问题来完成。

Minimize over w, b: ||w||^2
Subject to: y_i(w*x_i + b) ≥ 1, for all i = 1, ..., n

### 2.1.2 核技巧与非线性SVM

现实世界中的数据往往是线性不可分的，这个时候就需要非线性SVM登场了。核技巧是处理非线性问题的关键技术之一。它通过将原始数据映射到高维空间，来在高维空间中寻找线性可分的超平面。但是，直接在高维空间中进行计算是非常耗时的，核技巧通过对偶问题的核函数来避免这种高昂的计算成本。

核函数能够有效地计算高维空间中的点积，而无需显式地映射数据。常用的核函数包括线性核、多项式核、径向基（RBF）核和sigmoid核。通过选择合适的核函数和调整参数，非线性SVM能够在各种复杂度的数据上取得良好的分类效果。

from sklearn.svm import SVC
from sklearn.datasets import make_classification

# 创建非线性可分的模拟数据
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_clusters_per_class=1, random_state=4)

# 使用RBF核的SVM模型
model = SVC(kernel='rbf')
model.fit(X, y)

## 2.2 SVM的优缺点与应用场景

### 2.2.1 SVM的性能优势

SVM之所以成为机器学习领域的宠儿，很大程度上得益于其在小样本数据集上的优秀表现。当数据集规模较小时，SVM往往能够获得比其他算法更好的泛化能力。其最大间隔原则让模型对异常值具有一定的鲁棒性，这在一定程度上提高了模型的可靠性。此外，通过使用不同的核函数，SVM可以适应各种复杂的数据结构，包括非线性问题。

### 2.2.2 SVM在现实问题中的局限性

尽管SVM在某些方面表现出色，但它也有局限性。首先，SVM的计算复杂度较高，特别是在处理大规模数据集时，训练速度可能显著降低。其次，SVM的参数调整是一个挑战，尤其是当核函数和正则化参数都需要选择时。还有，SVM对于数据预处理非常敏感，比如需要仔细地特征缩放和归一化，否则可能导致模型性能不佳。

## 2.3 SVM的实战演练

### 2.3.1 SVM分类器的实现与调优

要实现一个SVM分类器，我们可以使用像scikit-learn这样的库来简化操作。下面是一个简单的例子，展示了如何使用Python和scikit-learn来构建一个SVM分类器，并通过网格搜索对模型进行调优。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.svm import SVC
from sklearn.metrics import classification_report

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建SVM分类器
svc = SVC()

# 使用网格搜索寻找最佳参数
parameters = {'kernel':('linear', 'rbf'), 'C':[1, 10]}
svc_search = GridSearchCV(svc, parameters, cv=5)
svc_search.fit(X_train, y_train)

# 输出最佳参数和分类结果
print("Best parameters found: ", svc_search.best_params_)
print("Classification report for best parameters:")
print(classification_report(y_test, svc_search.predict(X_test)))

### 2.3.2 SVM回归的实现与案例分析

SVM不仅可以用于分类问题，还可以通过修改为支持向量回归（SVR）来处理回归问题。SVR的目标是找到一个函数，尽可能在误差范围内拟合到数据的分布。下面是一个使用SVR进行房价预测的简单例子。

from sklearn.datasets import load_boston
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

# 加载数据集
boston = load_boston()
X, y = boston.data, boston.target

# 标准化特征数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)

# 创建SVR模型并拟合数据
svr = SVR(kernel='rbf', C=1.0, epsilon=0.2)
svr.fit(X_train, y_train)

# 预测测试集并计算均方误差
y_pred = svr.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

在这个例子中，我们使用了波士顿房价数据集，并对数据进行了标准化处理。通过选择合适的核函数和参数，SVR模型对房价进行回归分析。通过均方误差我们可以评估模型预测的准确性。

# 3. 决策树算法的原理与应用

## 3.1 决策树的工作机制

### 3.1.1 树结构的构建过程

决策树是一种经典的分类与回归方法，通过将数据集的特征分裂成多个区间，使得每个区间的样本尽可能属于同一类别（分类问题）或具有相似的输出值（回归问题）。构建决策树的过程涉及到特征选择、节点划分以及树的停止条件。

在构建决策树时，信息增益、基尼指数、均方误差等是常用的分裂标准。以信息增益为例，核心思想是选择信息增益最大的特征进行分裂，以期得到最大程度的纯度提升。信息增益的计算公式如下：

信息增益 = 熵(父节点) - [加权平均熵(子节点)]

其中，熵是度量数据集纯度的指标，信息增益越大，说明利用该特征进行数据划分后，数据的纯度提升得越多。

**代码示例：使用ID3算法计算信息增益**

import numpy as np

# 以简单的数据集为例，计算信息增益
def calculate_entropy(data):
    label_counts = np.bincount(data)
    entropy = -np.sum([(count / np.sum(label_counts)) * np.log2(count / np.sum(label_counts)) for count in