【Python树结构扩展】：多叉树在JSON数据转换中的巧妙应用

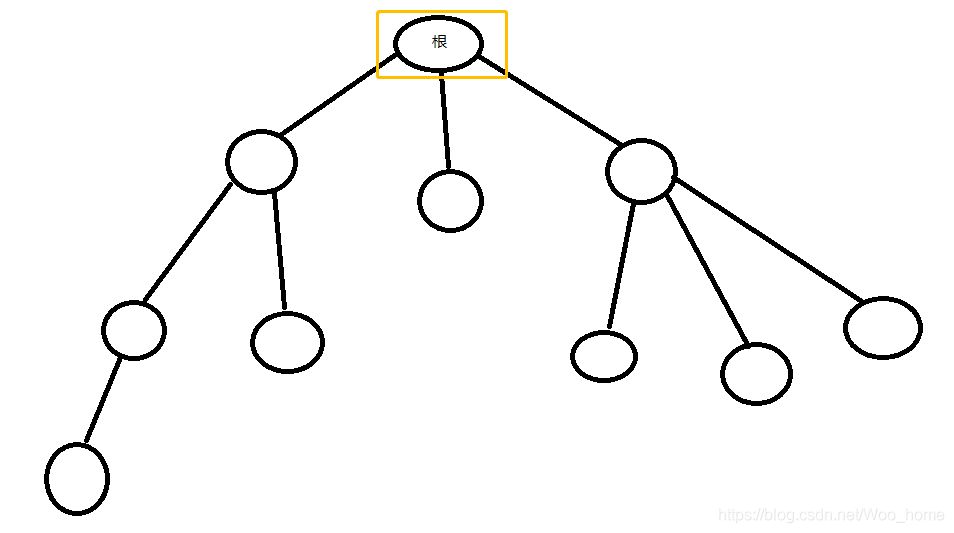
# 1. 多叉树数据结构概述

多叉树是一种非线性数据结构，与二叉树类似，但是每个节点可以有无限数量的子节点。它被广泛应用于计算机科学中，用于表示具有层次结构的数据。多叉树的每个节点通常包含一些数据和指向其子节点的指针。这种结构非常适合表示具有多对多关系的数据，如文件系统的目录结构，以及用于解析和生成JSON数据。

多叉树在操作和查询方面提供了灵活性，允许更高效的插入和删除操作，以及更复杂的数据遍历算法。在本章中，我们将初步介绍多叉树的基本概念和重要性，并为后续章节中深入探讨其理论和应用打下基础。

# 2. 多叉树的基本理论和操作

### 2.1 多叉树的定义和特性

#### 2.1.1 多叉树的定义

多叉树（M-ary Tree）是树结构的一种扩展，与二叉树类似，但它每个节点的子节点数量不限于两个。在多叉树中，一个父节点可以有零个或多个子节点。当多叉树中的所有节点最多只有m个子节点时，这样的树被称为m叉树。多叉树广泛应用于计算机科学中，尤其是人工智能领域，如决策树、XML文档结构等。

在多叉树的定义中，我们需要考虑以下几点：

- **节点（Node）**：树中的每一个数据单元。
- **边（Edge）**：连接父节点和子节点的线段。
- **根节点（Root）**：多叉树中的最顶层节点，不存在父节点。
- **叶子节点（Leaf）**：没有子节点的节点。
- **子树（Subtree）**：任何节点及其后代构成的树。
- **深度（Depth）**：从根节点到某一节点的路径长度。
- **高度（Height）**：从某一节点到其最远叶子节点的路径长度。

#### 2.1.2 多叉树的特性与分类

多叉树的特性包括：

- **非线性结构**：多叉树不是线性结构，因为它允许节点有更多的连接。
- **层次性**：节点之间具有明确的层次关系，每一层的节点是同级的。
- **分支性**：每个节点都可能有多个子节点，形成分支结构。
- **递归性质**：多叉树可以通过递归方式定义和处理。

根据结构的不同，多叉树可以分为以下几种类型：

- **完全多叉树（Complete M-ary Tree）**：除最后一层外，每一层都被完全填满，且最后一层的所有节点都尽可能地靠左。
- **完美多叉树（Perfect M-ary Tree）**：所有叶子节点都在同一层级上，每个非叶子节点都有m个子节点。
- **平衡多叉树（Balanced M-ary Tree）**：任何两个叶子节点之间的高度差不超过1。
- **非平衡多叉树（Unbalanced M-ary Tree）**：树的任何两个叶子节点之间的高度差大于1。

### 2.2 多叉树的基本操作

#### 2.2.1 节点的添加与删除

在多叉树中，节点的添加和删除是基本操作，但与二叉树相比，操作更为复杂，需要考虑子节点的数目和树的平衡问题。

**节点的添加**：

1. 确定添加位置，通常是叶子节点的子节点位置。
2. 创建新节点，并将其作为目标父节点的子节点。
3. 根据需要调整树的结构，如进行树的平衡处理。

class MTreeNode:
    def __init__(self, value):
        self.value = value
        self.children = []

    def add_child(self, child_node):
        self.children.append(child_node)

# 示例：向多叉树添加节点
root = MTreeNode('root')  # 创建根节点
child = MTreeNode('child')  # 创建子节点
root.add_child(child)  # 将子节点添加到根节点

**节点的删除**：

1. 查找要删除的节点。
2. 如果删除的是非叶子节点，需要确定如何处理其子节点（如删除子节点或重新分配）。
3. 删除节点，并保持树的其他属性不变。

def remove_node(node_to_remove):
    parent = find_parent(node_to_remove)
    if parent is not None:
        parent.children.remove(node_to_remove)
    # 如果删除的是根节点，需要特别处理
    if node_to_remove is root:
        root = None

# 注意：这个示例中的find_parent函数需要自己实现，用于查找父节点。

#### 2.2.2 树的遍历算法

多叉树的遍历算法可以分为三类：前序遍历、中序遍历、后序遍历。这些遍历方式与二叉树类似，但适用于多个子节点的情况。

**前序遍历**：先访问根节点，然后访问所有子节点。

def preorder_traversal(node):
    if node is None:
        return
    # 访问根节点
    print(node.value)
    # 前序遍历子节点
    for child in node.children:
        preorder_traversal(child)

**中序遍历**：先访问子节点，然后访问根节点。

def inorder_traversal(node):
    if node is None:
        return
    # 中序遍历子节点
    for child in node.children:
        inorder_traversal(child)
    # 访问根节点
    print(node.value)

**后序遍历**：先访问所有子节点，最后访问根节点。

def postorder_traversal(node):
    if node is None:
        return
    # 后序遍历子节点
    for child in node.children:
        postorder_traversal(child)
    # 访问根节点
    print(node.value)

#### 2.2.3 树的平衡与优化

多叉树的平衡与优化是维持树性能的关键。对于多叉树，我们通常关注的是树的高度平衡，以保证操作的时间复杂度不会因为树的倾斜而变得过高。

**平衡树的概念**：

平衡树指的是一棵树，其中任何两个叶子节点之间的高度差都不超过一个给定的常数。在二叉树中，这个概念与AVL树和红黑树紧密相关。对于多叉树，概念可以类推。

**平衡多叉树的实现**：

实现平衡多叉树通常需要自定义一个平衡操作，比如在节点添加或删除后进行平衡检查，并执行旋转等操作以维持树的平衡。

def balance_tree(node):
    # 这里需要实现树平衡的逻辑，包括检查树是否不平衡
    # 以及执行旋转等平衡操作。
    pass

平衡操作通常涉及到树的旋转，需要在添加或删除节点后调整子树的位置。对于多叉树，旋转操作较为复杂，需要考虑多个子节点的情况。

通过上述基本理论和操作的讨论，我们已经构建了对多叉树的初步认识，接下来的章节，我们将深入探讨多叉树与JSON数据结构的转换实践，以及多叉树在数据处理中的高级应用。

# 3. JSON数据格式解析

在现代网络应用中，数据传输是不可或缺的一部分。JSON（JavaScript Object Notation）是一种轻量级的数据交换格式，易于人阅读和编写，同时也易于机器解析和生成。尽管它源于JavaScript，但JSON是一种独立于语言的数据格式。本章节将详细介绍JSON数据格式，包括其基本的数据类型、组织方式，以及在Python中的处理方法。

## 3.1 JSON数据结构简介

### 3.1.1 JSON数据类型

JSON数据类型主要包括基本数据类型和复合数据类型。基本数据类型包括字符串（string）、数值（number）、布尔值（true或false）、null。复合数据类型则包括对象（object）和数组（array）。对象由一系列的“键值对”组成，格式为`{"key": "value"}`；数组则是值的有序列表，格式为`["value1", "value2", ...]`。

### 3.1.2 JSON数据的组织方式

在JSON中，数据的组织方式非常灵活，可以嵌套使用各种类型。例如，对象可以包含多个键值对，每个键值对的值可以是基本数据类型、数组、甚至另一个对象。这种嵌套的数据结构可以构建复杂的数据关系模型。

{
    "name": "John Doe",
    "age": 30,
    "isEmployed": true,
    "address": {
        "street": "123 Main St",
        "city": "Anytown",
        "zipcode": "12345"
    },
    "phoneNumbers": [
        {
            "type": "home",
            "number": "212 555-1234"
        },
        {
            "type": "office",
            "number": "646 555-4567"
        }
    ]
}

在上述JSON示例中，`address`是一个对象，而`phoneNumbers`是一个数组，数组中的每个元素都是一个包含`type`和`number`的对象。

## 3.2 JSON与Python的数据交换

JSON和Python之间的数据交换是通过Python标准库中的`json`模块实现的。Python中处理JSON数据的主要方法包括将Python数据结构转换为JSON格式，以及从JSON格式解析数据到Python对象。

### 3.2.1 Python中的JSON库

Python的`json`模块提供了编码（序列化）和解码（反序列化）JSON数据的功能。它可以处理Python中的基本数据类型和复合数据类型，包括列表、字典、元组、整数、浮点数、字符串等。

### 3.2.2 将Python数据结构转换为JSON

要将Python数据结构转换为JSON，可以使用`json.dumps()`方法。该方法接受一个Python对象并返回一个JSON格式的字符串。

import json

python_data = {
    "name": "John Doe",
    "age": 30,
    "isEmployed": True,
    "addre