图连通性探秘：无向与有向图连通组件解决方案

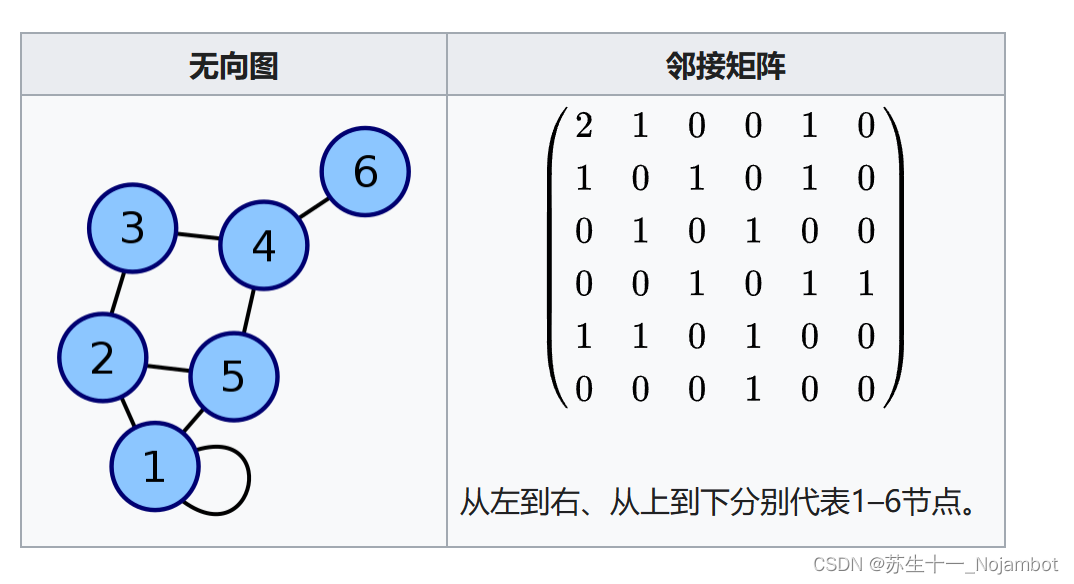
# 1. 图连通性的基础概念

在本章中，我们将探索图论中的基础概念，特别是与图连通性相关的术语和原理。首先，图是由顶点（节点）和边组成的数学结构，它能够模拟各种对象之间的复杂关系。连通性是指在一个图中，能否从一个顶点到达另一个顶点的属性。理解图连通性的基础对于后续章节中对算法的研究至关重要。

## 1.1 图的定义和性质

图G由顶点集V和边集E组成，可表示为G=(V,E)。一个顶点称为孤立的如果它没有任何边与其相连。无向图的边不区分方向，而有向图的边则是有方向的。

## 1.2 连通和非连通图的区别

在无向图中，如果任意两个顶点之间至少存在一条路径相连，则称该图是连通的。反之，如果存在至少一个顶点无法到达其他所有顶点，则该图是非连通的。连通性是图论研究中的核心概念之一，它直接关系到图的结构完整性和信息流动的能力。

通过掌握这些基础概念，读者将为深入学习图连通组件理论和算法打下坚实的基础。接下来的章节中，我们将详细探讨无向图和有向图的连通组件及其相应的算法。

# 2. 无向图的连通组件理论与算法

无向图是图论中一个重要的概念，它由顶点集合和连接顶点的边集合组成，是构建复杂网络结构的基础。在无向图中，边是没有方向的，即如果顶点A和顶点B之间存在一条边，那么顶点B和顶点A之间也存在一条边。理解无向图的连通性是分析图的基本性质和设计图算法的前提。

## 2.1 无向图连通性基础

### 2.1.1 无向图的定义和性质

无向图G可以表示为G=(V, E)，其中V代表顶点集合，E代表边集合。边e属于E，可以是(V[i], V[j])的形式，表示顶点i和顶点j之间有一条无向边。如果任意两个顶点之间都可以通过边到达，那么这个无向图就是连通的。反之，如果存在至少一对顶点不能通过边互相到达，该无向图就是非连通的。

在连通的无向图中，任意两个顶点都存在路径连接，这意味着无向图的顶点可以被划分为一组连通子图，每个子图内部是连通的，而子图之间是不连通的。这些连通子图被称为无向图的连通分量。

### 2.1.2 连通和非连通无向图的区别

连通无向图的性质和非连通图有很大差别。在连通图中，最少边的数量等于顶点数减一（即n-1条边，对于n个顶点）。这是因为一个连通图可以被看作是一棵树，而任何一棵树至少有n-1条边。

而在非连通图中，顶点之间不能相互到达，存在至少一对顶点没有边相连。非连通图至少包含两个连通分量，它们之间没有边相连。

## 2.2 无向图连通组件的算法分析

### 2.2.1 深度优先搜索（DFS）算法解析

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。在图的上下文中，算法从某个顶点开始，沿着一条边尽可能深地搜索新的顶点，直到达到一个没有未探索的邻居的顶点为止，然后回溯。

为了寻找无向图的所有连通分量，可以从任何一个顶点开始执行DFS。以下是使用DFS寻找无向图连通分量的基本步骤：

1. 从图中的一个顶点v开始。
2. 将v标记为已访问，并将它加入当前连通分量。
3. 对每一个与v相连的顶点u执行以下步骤：
- 如果u未被访问过，则从u开始递归执行DFS。
4. 当前顶点v的所有邻居都被访问过之后，当前连通分量的搜索完成。
5. 重复步骤1-4，直到所有的顶点都被访问过。

下面是一个简单的DFS算法实现：

def dfs(graph, v, visited):
    visited[v] = True
    print(v, end=' ')
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)

# 示例图的邻接表表示
graph = {0: [1, 2], 1: [0, 3], 2: [0], 3: [1]}
visited = [False] * len(graph)

# 对每个未访问的顶点执行DFS
for i in range(len(graph)):
    if not visited[i]:
        dfs(graph, i, visited)

在这段代码中，我们用`visited`数组来跟踪每个顶点是否被访问过，以避免重复访问同一个顶点。`graph`是一个字典，键是顶点，值是一个列表，包含了与该顶点相邻的顶点。我们从顶点0开始执行DFS，并递归地访问所有未访问的相邻顶点。

### 2.2.2 广度优先搜索（BFS）算法解析

广度优先搜索（BFS）是一种遍历或搜索树或图的算法。在图的上下文中，算法从某个顶点开始，先访问所有邻接的顶点，然后对每一个邻接顶点，再访问其邻接顶点，如此迭代进行。

BFS同样适用于寻找无向图中的所有连通分量。其基本步骤如下：

1. 创建一个队列。
2. 将起始顶点v加入队列，并将其标记为已访问。
3. 当队列非空时执行以下步骤：
- 从队列中取出一个顶点u。
- 对每一个与u相邻的顶点w，如果w未被访问过，则将w加入队列，并标记为已访问。
4. 重复步骤3，直到队列为空。

BFS算法的Python实现代码如下：

from collections import deque

def bfs(graph, v):
    visited = set()
    queue = deque([v])
    visited.add(v)
    while queue:
        s = queue.popleft()
        print(s, end=' ')
        for i in graph[s]:
            if i not in visited:
                visited.add(i)
                queue.append(i)

graph = {0: [1, 2], 1: [0, 3], 2: [0], 3: [1]}
for i in graph:
    if i not in visited:
        bfs(graph, i)

在这段代码中，我们用`visited`集合来记录已经访问过的顶点，用队列`queue`来存储即将访问的顶点。我们从顶点0开始，逐个访问其邻接顶点，直到队列为空。

## 2.3 实践：无向图连通组件的编程实现

### 2.3.1 编程语言的选择与环境搭建

选择适合图算法编程实现的编程语言很重要。通常，C++、Python或Java是不错的选择，因为它们都支持高效的数据结构和算法实现，并且拥有丰富的库。对于本实践，我们选择使用Python进行实现，因为其简洁的语法和强大的库支持使得算法原型开发更加高效。

环境搭建主要包括安装Python解释器、必要的第三方库，例如`networkx`用于图的表示和操作，以及`matplotlib`用于绘图和可视化。可以通过包管理工具如pip来安装这些库。

### 2.3.2 算法实现与案例分析

让我们从一个实际案例开始，来实现无向图的连通组件查找。假设我们有如下无向图：

0 -- 1
|    |
|    |
2 -- 3

我们将创建一个图的表示，并使用DFS或BFS算法来找出所有连通分量。

Python代码示例（使用DFS）：

# 定义图的结构
graph = {
    0: [1, 2],
    1: [0, 3],
    2: [0],
    3: [1]
}

def find_connected_components(graph):
    visited = set()
    components = []
    for v in graph.keys():
        if v not in visited:
            connected_nodes = set()
            stack = [v]
            while stack:
                node = stack.pop()
                if node not in visited:
                    connected_nodes.add(node)
                    visited.add(node)
                    stack.extend(set(graph[node]) - connected_nodes)
            components.append(connected_nodes)
    return components

components = find_connected_components(graph)
print("连通分量：", components)

在这段代码中，我们遍历图中所有未访问的顶点，并使用DFS找出与每个顶点相连的所有顶点，直到没有新的顶点可以访问。最终的`components`列表包含了所有找到的连通分量。

这个过程不仅帮助我们理解算法的执行逻辑，还展示了如何将理论应用到实际问题中，这在IT行业中是一项极其重要的能力。通过对图连通性问题的深入分析和实践，我们可以构建更加高效和鲁棒的网