图社区检测深入：寻找图中隐藏的社区结构

# 1. 图社区检测概念与重要性

## 1.1 图社区检测简介

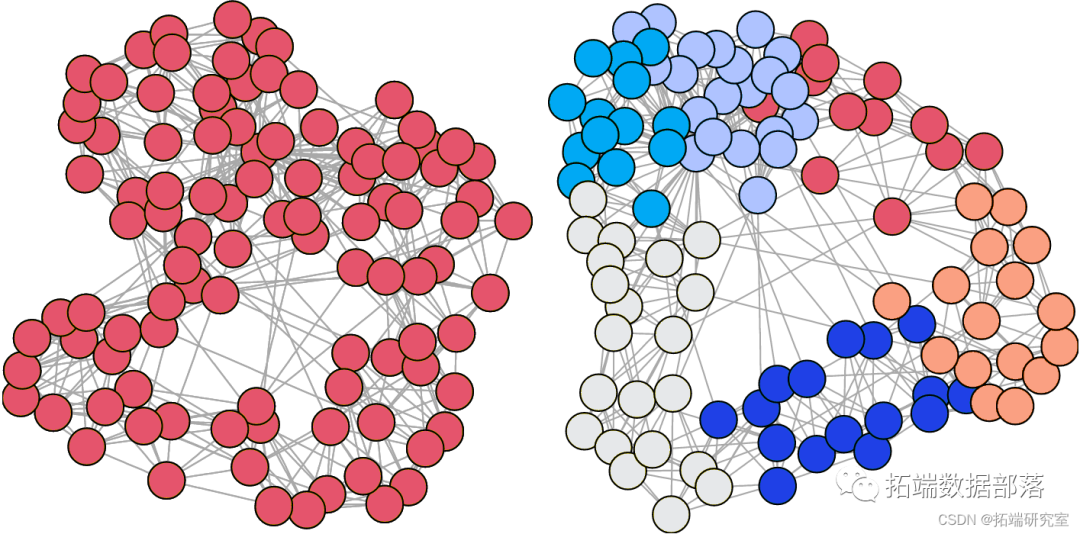
图社区检测是一种发现图结构中社区（即密集连接的节点子集）的过程，是网络科学和数据分析领域的核心概念。通过这种技术，我们可以理解复杂网络的内在结构和动态，比如社交网络、生物网络和交通网络等。

## 1.2 社区检测的重要性

社区检测对于网络分析至关重要，因为它能够揭示网络内部的群体划分，协助我们识别网络的层次性和模块化特征。此外，社区结构的发现还能应用于推荐系统、信息传播控制、网络结构优化等多个领域。

## 1.3 应用场景举例

在社交网络中，社区检测帮助我们发现兴趣小组或者潜在的社交圈子；在生物学领域，社区检测能够揭示蛋白质交互网络的结构特征；在网络安全中，社区检测可以辅助网络监控，发现异常行为。这些应用案例展示了社区检测在解决现实世界问题中的潜力和价值。

# 2. 图社区检测理论基础

### 2.1 图论的基本概念

#### 2.1.1 图的表示方法

图是图社区检测的基础，它由顶点（或节点）和边组成。在图论中，图的表示方法有多种，主要包括邻接矩阵和邻接表两种方式。

- **邻接矩阵**：邻接矩阵是一个二维数组，其大小为顶点数的平方。如果两个顶点之间存在边，则对应的矩阵元素为1，否则为0。邻接矩阵易于实现，并且可以直接用于表示有权重的图。但是，对于大规模图来说，邻接矩阵的存储空间要求较高。

- **邻接表**：邻接表是一系列链表或数组，每个顶点有一个链表来存储它所有的邻接点。这种表示方法节省空间，特别适合稀疏图的存储。邻接表虽然在某些操作上不如邻接矩阵直观，但可以通过链表快速访问顶点的邻接点。

#### 2.1.2 图的分类与特性

图可以分为有向图和无向图。有向图的边有方向性，表示为有序对(v1, v2)，而无向图的边没有方向，表示为无序对{v1, v2}。此外，图还可以根据边的权重被分类为有权图和无权图。有权图的边上带有权重，表示连接顶点间的关系强度或其他属性；无权图则不包含这些信息。

图的特性包括连通性、环、路径等。连通性描述图中顶点之间是否存在路径相连；环是指闭合路径；而路径是顶点序列中每对连续顶点间存在边的序列。在社区检测中，顶点和边的特性有助于确定社区的边界和结构。

### 2.2 社区结构的理论模型

#### 2.2.1 社区的定义与性质

社区是指图中顶点的一个子集，子集内的顶点之间的连接比与其他部分更紧密。社区的定义基于模块性，即图中同一社区内部的连接密度高于不同社区之间的连接密度。社区具有以下性质：

- **内聚性**：社区内部的顶点应有较高的连接密度。
- **排他性**：社区之间应有较低的连接密度。
- **层次性**：在某些情况下，社区结构可能表现出嵌套或层次关系，即一个社区内部可能包含更小的社区。

#### 2.2.2 社区检测的目标和挑战

社区检测的目标是从图中识别出符合上述性质的社区结构。挑战包括但不限于：

- **可扩展性**：如何有效处理大规模图中的社区检测问题。
- **动态性**：图的结构可能随时间变化，社区检测算法需要适应这种动态性。
- **多尺度性**：社区可能存在多个层次，算法需要能够识别出不同层次的社区结构。

### 2.3 社区检测的关键算法

#### 2.3.1 分层算法和模块度优化

分层算法是根据模块度优化原则来检测社区的算法。模块度是衡量图中社区划分好坏的一个标准，定义为图中实际观察到的内部边数量与随机情况下的期望边数量之差。模块度优化的目标是最大化模块度。

- **GN算法**：Girvan-Newman算法通过递归移除连接度最高的边来识别社区，直到达到稳定的社区结构。
- **模块度优化算法**：以模块度为优化目标，使用贪心算法或启发式算法来调整社区划分，以实现模块度最大化。

#### 2.3.2 聚类算法在社区检测中的应用

聚类算法是社区检测的另一类关键算法。它们被广泛应用于社区检测中，尤其是用于识别具有特定拓扑特征的社区结构。

- **谱聚类**：通过图的拉普拉斯矩阵特征向量来识别社区，它依赖于图的全局结构信息。
- **层次聚类**：一种按照层次结构来组织顶点的聚类方法，可以通过多种合并或分裂策略来形成社区结构。

下一章将详细探讨社区检测算法的实践分析，包括基于模块度优化的算法实践以及聚类算法在社区检测中的应用等。

# 3. 社区检测算法实践分析

## 3.1 基于模块度优化的算法实践

### 3.1.1 模块度的计算方法

模块度是衡量社区划分好坏的一个重要指标，它表示网络划分成模块后，模块内部的边数与随机网络中模块内部边数期望的差值。模块度的计算方法对于社区检测算法的性能至关重要。

在实践中，模块度的计算通常涉及以下步骤：

1. **构建邻接矩阵**：通过图的邻接矩阵来表示图中节点之间的连接关系。
2. **初始化社区**：随机或者根据特定策略初始化社区。
3. **计算模块度**：根据模块内边数和模块间边数与期望值的差异来计算模块度，常用的计算公式如下：

\[ Q = \frac{1}{2m} \sum_{i,j} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j) \]

其中，\( A_{ij} \)是邻接矩阵的元素，\( k_i \) 和 \( k_j \)是节点i和j的度，\( c_i \)和\( c_j \)是节点i和j所在的社区，\( m \)是图中边的总数，\( \delta \)是克罗内克函数，如果\( c_i \)和\( c_j \)相同则为1，否则为0。

### 3.1.2 算法实现与案例分析

为了实现模块度优化的社区检测算法，通常采用贪心算法来最大化模块度。算法实现步骤通常包括：

1. **初始化社区**：每个节点自成一个社区。
2. **合并社区**：尝试将两个社区合并，计算合并后的模块度变化。
3. **选择最优合并**：选取使模块度增加最大的社区合并，直到模块度不再增加。

通过下面的代码片段来展示一个基于贪心算法的模块度优化社区检测算法的Python实现：

import numpy as np

def compute_modularity(A, community):
    m = np.sum(A) / 2
    comm_size = np.bincount(community)
    k_in = np.array([np.sum(A[community == i, community == i]) for i in np.unique(community)])
    return np.sum(k_in - (k_in[:, None] @ k_in[None, :]) / (2 * m)) / m

def greedy_modularity_optimization(A):
    # 初始化社区为每个节点独立
    comm = np.arange(A.shape[0])
    max_modularity = compute_modularity(A, comm)
    # 迭代寻找最优社区划分
    while True:
        improved = False
        for i in range(len(comm)):
            for j in range(i+1, len(comm)):
                # 计算合并社区后的模块度
                comm_temp = comm.copy()
                comm_temp[comm == j] = i
                modularity = compute_modu