智能A*算法：图中最佳路径搜索终极指南

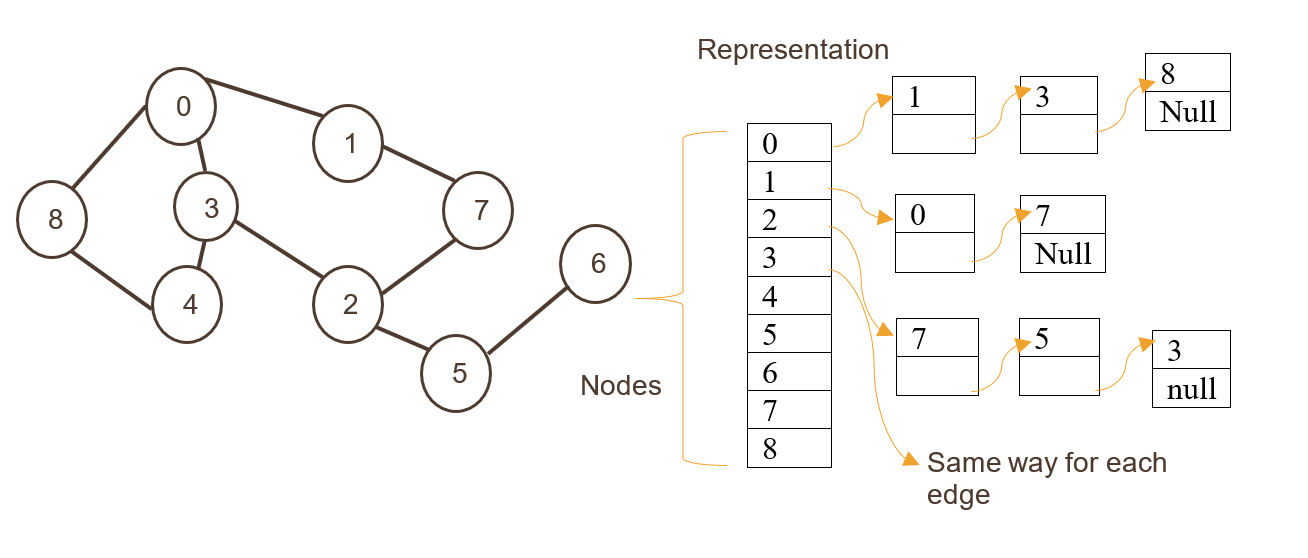
# 1. 智能A*算法概述

## 1.1 A*算法简介
A*算法是一种在图形平面上，有多个节点的路径中，寻找从初始节点到目标节点最低成本路径的算法。由于其高效性和准确性，它是游戏开发、机器人路径规划、以及各种图形界面应用中广泛使用的路径搜索算法。

## 1.2 A*算法的优势
它之所以备受青睐，主要得益于它的几个优点：首先，A*是完整的，意味着只要存在一条路径，它总能找出来。其次，A*算法是优化的，能够找到最优解。此外，它基于启发式的特性赋予了算法灵活性，使得它可以应用于各种复杂的环境中。

## 1.3 A*算法的应用场景
智能A*算法不仅适用于经典的二维网格搜索，还能适应三维空间搜索、网络路由、甚至在医疗诊断、市场分析等领域都有所应用。随着AI技术的发展，A*算法的应用场景还在不断扩大。

本章节为后续章节铺垫了基础，为理解A*算法的工作原理和实际应用打下了基础。在第二章，我们将深入探讨A*算法的理论基础，并具体分析其核心机制和性能影响因素。

# 2. A*算法的理论基础

### 2.1 A*算法核心概念

#### 2.1.1 启发式搜索和路径代价

在路径查找问题中，启发式搜索（heuristic search）是一种用于在图中寻找从起始节点到目标节点的最佳路径的策略。它利用启发函数（heuristic function），也称为评估函数，来估算从当前节点到目标节点的最佳路径成本。启发函数的目的是减少需要考虑的节点数量，以减少搜索空间，提高算法效率。

启发式搜索通常通过以下步骤实现：

1. **估计剩余距离：** 启发函数估计从当前节点到达目标节点的估计距离（h），这个距离是未知的，只能通过启发式信息来估计。
2. **实际距离：** 节点之间的实际移动距离（g），从起始节点开始，这个值随着路径的延伸而增加。
3. **总成本：** 将这两个值结合起来，得到评估函数 f(n) = g(n) + h(n)，其中 n 表示当前节点。在A*算法中，评估函数的总成本 f(n) 被用来决定节点扩展的顺序。

#### 2.1.2 评估函数和启发函数

评估函数是启发式搜索的核心，它决定了搜索的方向和优先级。评估函数 f(n) 是两个分量之和：g(n) 和 h(n)。

- **g(n)：** 从起始节点到当前节点 n 的实际代价。
- **h(n)：** 从当前节点 n 到目标节点的估计代价，也称为启发函数。

一个好的启发函数应该满足以下条件：

1. **可采纳性（Admissibility）：** 启发函数 h(n) 永远不会高估从节点 n 到目标节点的实际最低成本。如果满足这一条件，该启发式搜索被称为是可采纳的，而这样的启发函数称为乐观的。
2. **一致性（Consistency）/单调性：** 如果节点 n 到目标节点的直接代价是 c，对于任何节点 n 的任意后继节点 n'，通过边(n, n')的代价是 e，那么 h(n) <= c + h(n')。满足一致性条件的启发函数可以保证搜索树的分支不会在搜索过程中来回翻转。

### 2.2 A*算法的工作原理

#### 2.2.1 开放列表和封闭列表

在执行A*算法时，有两类重要的数据结构：开放列表（open list）和封闭列表（closed list）。

- **开放列表**：存储已经发现但尚未完全处理的节点。它通常按 f(n) 值排序，使得算法能够优先处理 f(n) 值最小的节点。
- **封闭列表**：存储已经评估过的节点，确保每个节点不会被重复处理。

算法的每一步都遵循以下流程：

1. 将起始节点加入开放列表。
2. 如果开放列表为空，则算法终止，没有找到路径。
3. 从开放列表中移除具有最小 f(n) 值的节点作为当前节点。
4. 将当前节点加入封闭列表。
5. 检查当前节点是否是目标节点。如果是，则回溯路径并终止算法。
6. 生成当前节点的所有后继节点。
7. 对于每个后继节点，如果它不在封闭列表中，并且没有更好的路径（通过比较 f(n)）存在，则将其添加到开放列表。

#### 2.2.2 节点的评估和扩展

节点的评估和扩展是A*算法的核心操作，直接影响到算法的效率和最终结果。

节点的评估函数 f(n) = g(n) + h(n)，其中 g(n) 是从起始节点到当前节点 n 的实际代价，h(n) 是从当前节点 n 到目标节点的估计代价。在评估节点时，如果一个节点从未被访问过，或已经从封闭列表中移除，那么该节点会被添加到开放列表中。

在扩展节点时，每个节点会生成其后继节点（通常是相邻节点），并计算每个后继节点的 f(n) 值。如果后继节点已存在于开放列表中，会检查当前 g(n) 值是否比已有的 g(n) 更低（即是否有更好的路径）。如果是，则更新该节点的 g(n) 和 f(n) 值。如果后继节点在封闭列表中，则忽略它，因为该节点已处理过。

每个节点按照其 f(n) 值进行排序，使得算法总是首先考虑 f(n) 值最低的节点，这通常是到达目标成本最小的路径。

#### 2.2.3 算法的终止条件

A*算法主要有两种终止条件：

1. **找到目标：** 当算法在开放列表中找到目标节点时，算法终止。此时，可以回溯路径到起始节点以构造完整的路径。
2. **开放列表为空：** 如果在达到目标之前开放列表被耗尽，说明没有找到从起始节点到目标节点的路径。这可能是因为图中没有路径，或者搜索空间无法触及目标节点。

### 2.3 A*算法的性能分析

#### 2.3.1 时间复杂度和空间复杂度

A*算法的时间复杂度和空间复杂度受到多种因素影响，包括图的大小、节点的分支因子（即每个节点的后继节点数量）、以及启发函数的选择。

- **时间复杂度：** A*算法的时间复杂度通常取决于开放列表和封闭列表中的节点数量。在最坏的情况下，每一条边都会被考察一次，因此时间复杂度通常与边的数量成正比。对于稀疏图，时间复杂度接近 O(E)，其中 E 是边的数量。在密集图中，时间复杂度可以近似为 O(N log N)，其中 N 是节点的数量，因为开放列表的管理成本较高。
- **空间复杂度：** 空间复杂度主要受到开放列表和封闭列表大小的影响。算法需要存储所有已发现但尚未处理的节点以及已处理过的节点，因此空间复杂度为 O(N + E)，在实践中通常更接近于 O(N)，因为每条边最多涉及两个节点。

#### 2.3.2 启发函数的选择对性能的影响

启发函数 h(n) 的选择对A*算法的性能有很大影响。

- **启发函数过高估计：** 如果 h(n) 高估了实际成本，可能会导致算法过早地摒弃更优的路径，或者在开放列表中保留过多的节点，从而增加搜索时间。
- **启发函数过低估计：** 如果 h(n) 低估了实际成本，算法可能会退化成 Dijkstra 算法，失去启发式的优势。
- **理想情况：** 最理想的启发函数 h(n) 正好等于从节点 n 到目标节点的实际成本，但这种情况在实际中很难实现。通常需要对问题的结构和特性有一定的了解，才能设计出较好的启发函数。

选择一个好的启发函数能够显著提高A*算法的效率。在实践中，启发函数往往基于领域知识来设计，例如在地图导航中，直线距离是常用的启发函数。在其他问题中，可能需要通过实验和分析来确定最佳的启发式方法。

下面，我们将详细探讨A*算法在不同领域的实践应用，包括在编程实现和具体应用案例中的细节。

# 3. A*算法的实践应用

## 3.1 实现A*算法的编程准备
在实际编写A*算法之前，需要对编程环境和数据结构有清晰的认识。这将确保我们能够正确地实现算法，并理解可能影响性能的内在因素。

### 3.1.1 数据结构的选择和定义

选择合适的数据结构是实现A*算法的关键。一般来说，需要以下几个主要的数据结